机器学习之层次聚类与K-Means

聚类与分类不同，聚类是针对给定的样本，依据他们的相似程度或距离，将其归为若干个类或簇的数据分析问题，属于无监督学习。聚类算法是在聚类之前并没有标签，之后聚类之后才会知道它属于哪个类别。本博客仅介绍两种常见的聚类算法：层次聚类和Kmeans聚类。

一、层次聚类

层次聚类具有聚合（自下而上）和分裂（自上而下）两种方法。聚合法是将样本各自分到一个类，之后将相距最近的两类合并成新的类，重复此步骤直至满足条件，得到层次化的类别。分裂法是将所以样本分到一个类，之后将距离最远的样本分到两个新的类，重复此步骤直至满足条件，得到层次化的类别。

• 聚合聚类基本过程：
  • 输入：n个样本组成的样本集合及样本间的距离
  • 输出：对样本集合的一个层次化聚类
  • （1）计算n个样本两两之间的欧氏距离；
  • （2）构造n个类，每个类只包含一个样本；
  • （3）合并类间距离最小的两个类，其中最短距离为类间距离，构建一个新类；
  • （4）计算新类与当前各类的距离，若类的个数为1，终止计算，否则返回到步骤（3）。

例子

给定5个样本的集合，样本间的欧氏距离如下矩阵D所示：其中$d_{i}j$为第i个样本与第j个样本间的欧氏距离。显然D为对称矩阵。利用聚合层次聚类法对五个样本进行聚类。
$$D=[d_{ij}{]}_{5\ast 5}\left[\begin{array}{ccccc}0& 7& 2& 9& 3\\ 7& 0& 5& 4& 6\\ 2& 5& 0& 8& 1\\ 9& 4& 8& 0& 5\\ 3& 6& 1& 5& 0\end{array}\right]$$
（1）首先用5个样本构成5个类，$G_i=x_i,i=1,2,3,4,5$，这样，样本间的距离即为类别间距。
（2）由矩阵D可知 $d_{3}5$=$d_{5}3$=1最小，所以把$G_3$和$G_5$合并为一个新类，记为$G_6=\{x_3,x_5\}$
（3）继续计算新类与其余类间的距离：$d_{61}=2,d_{62}=5,d_{64}=5,d_{12}=7,d_{14}=9,d_{24}=4$,最小的是类6和类1间距离为2，因此将类6和类1归为新的类，记为$G_7=\{x_1,x_3,x_5\}$。这里简单说一下$d_{61}=2$的由来:因为$d_{13}=2,d_{15}=3$,2<3，所以$d_{61}=2$=$d_{31}$。其余同理。
（4）计算$G_7$与$x_2,x_4$间的距离，$d_{72}=5,d_{74}=5,d_{24}=4$，将$x_2,x_4$归为一类，即$G_8=\{x_2,x_4\}$。
（5）到现在为止，5个样本形成了两个类，分别为$G_7=\{x_1,x_3,x_5\}$,$G_8=\{x_2,x_4\}$，继续将$G_7,G_8$归为一类，记为$G_9$。全部样本已经归为同一类，终止聚类。

• 上面的层次聚类过程可以用下面的层次聚类图（用python画出）表示：
  

二、Kmeans

k均值聚类是基于中心的聚类算法，通过迭代，将样本分到k个类中，使每个样本与其所属类的中心或均值最近，得到k个非层次化的类别，构成对空间的划分。

• 基本步骤：
  • 输入：n个样本的集合
  • 输出：样本集合的聚类
  • （1）初始化。需将数据标准化，随机选择k个样本作为初始聚类中心；
  • （2）对样本进行聚类。计算每个样本到类中心的距离，将样本划分到与其最近的类别中，构成新的聚类结果；
  • （3）计算新的聚类中心。对聚类结果，计算各个类中的样本的均值，作为新的类中心；
  • （4）如果迭代收敛（聚类结果不再变化）或符合终止条件，输出聚类结果。

例子

给定含有5个样本的集合：
$$X=\left[\begin{array}{ccccc}0& 0& 1& 5& 5\\ 2& 0& 0& 0& 2\end{array}\right]$$
试用Kmeans均值聚类算法将样本聚类到两个类别中。
解：
（1）先确定两个初始聚类中心，假设选择$x_1=(0,2{)}^T,x_2=(0,0{)}^T$，分别为类别$G_1,G_2$;
（2）计算各样本到聚类中心的欧式距离的平方（方便计算）并进行归类：
$d_{13}=5,d_{23}=1$，将$x_3$划分到$G_2$类中；
$d_{14}=29,d_{24}=25$，将$x_4$划分到$G_2$类中；
$d_{15}=25,d_{25}=29$，将$x_5$划分到$G_1$类中；
得到新的类别：$G_1=\{x_1,x_5\}$，$G_2=\{x_2,x_3,x_4\}$
（3）计算新的聚类中心。$G1=(2.5,2{)}^T，G2=(2,0{)}^T$
（4）计算各样本到新聚类中心的距离： 现在的G类为空了，但是有聚类中心，重新聚类
$d_{11}=6.25,d_{12}=8$，将$x_1$划分到$G_1$类中；
$d_{21}=10.25,d_{22}=4$，将$x_2$划分到$G_2$类中；
$d_{31}=6.25,d_{32}=1$，将$x_3$划分到$G_2$类中；
$d_{41}=10.25,d_{42}=9$，将$x_4$划分到$G_2$类中；
$d_{51}=6.25,d_{52}=13$，将$x_5$划分到$G_1$类中；
得到新的类别：$G_1=\{x_1,x_5\}$，$G_2=\{x_2,x_3,x_4\}$ 聚类结果不变，聚类终止。
最终聚类结果即为$G_1=\{x_1,x_5\}$，$G_2=\{x_2,x_3,x_4\}$。

三、python实战

3.1、层次聚类

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.cluster.hierarchy as sch   # 
from sklearn.cluster import AgglomerativeClustering

disMat = np.array([[0,7,2,9,3],
                   [7,0,5,4,6],
                   [2,5,0,8,1],
                   [9,4,8,0,5],
                   [3,6,1,5,0]])
Z = sch.linkage(disMat,method='ward')
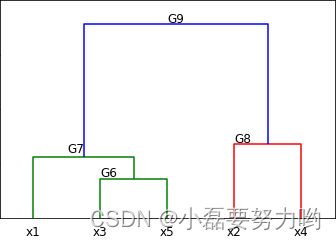
sch.dendrogram(Z,labels=list(['x1','x2','x3','x4','x5']))
plt.text(15,3.8,'G6',fontdict={'size':12})
plt.text(10,6,'G7',fontdict={'size':12})
plt.text(35,7,'G8',fontdict={'size':12})
plt.text(25,18,'G9',fontdict={'size':12})
plt.yticks(range(0,23,5))
plt.show()  # 图即为上面的层次聚类图

# # euclidean欧式距离  ward合并的类的方差最小化  n_clusters=3 分为三类
ac = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward')
ac.fit(disMat)
labels = ac.fit_predict(disMat)
print(labels) # [0 2 0 1 0]   x1,x3,x5为一类;x2为一类;x4为一类; 与上面我们计算的分类一致。

3.2、Kmeans

K值的确定：手肘法

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn import preprocessing

df = pd.read_csv('K-Means数据集.txt',sep='\t',header=None,usecols=[0,1,2],names=['a','b','c'])
x = preprocessing.StandardScaler().fit_transform(df[['a','b']]) # 只要两个特征

klist = []
for k in range(1,10):
    kmn=KMeans(n_clusters=k)
    kmn.fit_predict(x)
    klist.append(kmn.inertia_)   # 误差平方和
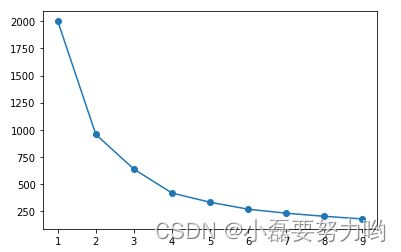
plt.plot(range(1,10),klist,marker='o')   # 当k= 4的时候逐渐平缓 所以我们选择k=4

2个特征聚类可视化

kmn=KMeans(n_clusters=4)
res=kmn.fit_predict(x)
lable_pred=kmn.labels_     # 聚类的标签即类别
centers=kmn.cluster_centers_  # 聚类中心
print(centers)
# 四个类别的聚类中心
[[-0.9961586  -0.87182378]
 [ 1.60044603  0.90738041]
 [-0.11462682  0.86531506]
 [ 0.57360717 -0.76353259]]


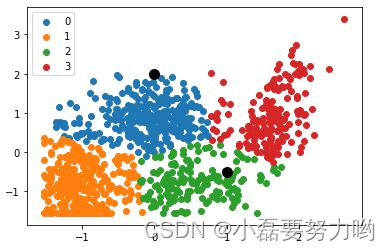
# 对两个点进行预测 类别分别为0 和 2 下面可视化 将两个点也加了进去 预测准确
kmn.predict([[0,2],[1,-0.5]])  # array([0, 2]) 

plt.scatter(x[x['y']==0]['a'],x[x['y']==0]['b'],label=0)
plt.scatter(x[x['y']==1]['a'],x[x['y']==1]['b'],label=1)
plt.scatter(x[x['y']==2]['a'],x[x['y']==2]['b'],label=2)
plt.scatter(x[x['y']==3]['a'],x[x['y']==3]['b'],label=3)
plt.scatter(x=0,y=2,marker='o',color='k',s=100)
plt.scatter(x=1,y=-0.5,marker='o',color='k',s=100)
plt.legend()
plt.show()

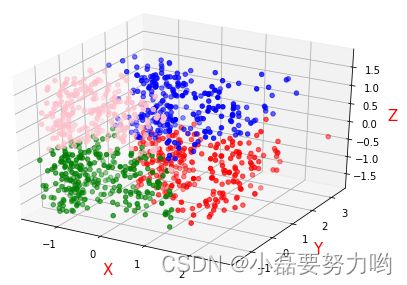
3个特征聚类可视化

from mpl_toolkits.mplot3d import Axes3D  # 空间三维画图
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

df = pd.read_csv('K-Means数据集.txt',sep='\t',header=None,usecols=[0,1,2],names=['a','b','c'])
x = preprocessing.StandardScaler().fit_transform(df)

estimator=KMeans(n_clusters=4)
res=estimator.fit_predict(x)
lable_pred=estimator.labels_
centers=estimator.cluster_centers_
inertia=estimator.inertia_
print(centers) # 聚类中心
[[-0.67604892 -0.78556506  0.90579587]
 [ 0.50573115  0.70181006  0.90113919]
 [ 0.78663516  0.87904113 -0.80456021]
 [-0.61783656 -0.78968316 -0.84178368]]

x = pd.DataFrame(x)
x.columns = ['a','b','c']
x['y'] = lable_pred

x = pd.DataFrame(x)
x.columns = ['a','b','c']
x['y'] = lable_pred

fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x[x['y']==0]['a'],x[x['y']==0]['b'],x[x['y']==0]['c'],color='red')
ax.scatter(x[x['y']==1]['a'],x[x['y']==1]['b'],x[x['y']==1]['c'],color='blue')
ax.scatter(x[x['y']==2]['a'],x[x['y']==2]['b'],x[x['y']==2]['c'],color='green')
ax.scatter(x[x['y']==3]['a'],x[x['y']==3]['b'],x[x['y']==3]['c'],color='pink')
# 添加坐标轴(顺序是Z, Y, X)
ax.set_zlabel('Z', fontdict={'size': 15, 'color': 'red'})
ax.set_ylabel('Y', fontdict={'size': 15, 'color': 'red'})
ax.set_xlabel('X', fontdict={'size': 15, 'color': 'red'})
# 展示
plt.show()