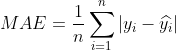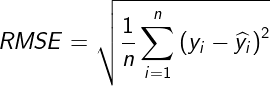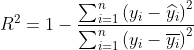机器学习中分类任务和回归任务中的评价指标

1 分类问题的评价指标

1.1 Accuracy

Accuracy(精度)，计算方法为：

                                                           

对于模型预测结果，判断正确记1，判断错误记0，所以Acc表示模型预测正确的样本数占样本总数的比例，取值为 0-1 ，越接近 1，说明模型的效果越好。就是错误率。

对输出的每个类别惩罚都一样，但是在很多实际问题中，我们认为做出某种错误判断代价会大一些。比如银行要对贷款人进行信用评估，这里会出现两种错误：①贷款人具有还款能力，但是被判断为没有还款能力；②贷款人没有还款能力，但是被判断为具有还款能力。如果贷款机构想尽量规避风险，那么在训练模型的时候就应该加大对第②种情况的惩罚。

1.2 Precision

首先说明一下混淆矩阵，下图截自西瓜书：

根据表格先琢磨一下  都表示什么意思，这里有点绕。

Precision(查准率 / 准确率)，计算方法为：

                                                            

查准率表示预测为正例的样本中，预测正确的比例。举个例子，我们模型对200个样本进行预测，预测结果是120个正例，80个反例。那么在我们预测为正例的这120个样本中，假设有100个为正例，20个为反例，那么查准率就是  。

1.3 Recall

Recall(查全率 / 召回率)，计算方法为：

                                                            

查准率表示预测为正例的样本中，预测正确的比例。还是上面例子，我们有200个样本，这200个样本中有110个正例，90个反例。我们模型对这200个模型进行预测，假如样本中的110个正例，模型将其100个预测为正例，剩下10个预测为反例，那么查全率就是 。

1.4 P-R曲线

机器学习中，准确率和召回率是一个此消彼长的存在，通过P-R曲线应该好理解一点（随手画了一个帮助理解，原谅手拙）。

我们可以这样理解，对于我们需要预测的样本，模型对他们进行一个排序，将最有可能被预测为正类的样本排在第一个，最不可能预测为正类的样本排在最后一个。

首先我们将排在第一的样本预测为正类，剩下全部样本预测为反类。这个时候我们的准确率（P）就一定是最高的：要么是1（预测正确），要么是0（预测错误，但是既然最有可能为正类的都不是正类的话，那么这个模型一定是有问题的，所以不考虑）；此时我们的召回率（R）就会比较低，因为我们可能有众多正例，而我们只预测出了一个。

接下来我们把排在前两位的样本预测为正类，剩下的预测为反类，这个时候准确率（P）可能就还是为1，可能变成0.5（第二个样本预测错误了，但是这种情况一般也比较少见）。同时，召回率（R）就可能上升了，就是说，我们有很多正例，刚才值预测出了一个，现在预测出了两个。

以此类推，这样一直下去，随着P的下降，R会上升。以横轴为R，纵轴为P，就画出了上面这个P-R曲线。当样本量很大的时候，曲线就趋于光滑，就变成下图这样了（截自西瓜书）。

关于这张图，还有几点需要说明。上图A，B，C分别代表三个模型的P-R曲线。我们训练一个模型，当然是希望它的准确率和召回率都比较好，所以显然A，B模型的性能比C要好一些（P和R都更高）。对于A，B模型的比较，我们有其他方法。

1.5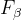   

对于上面A，B，我们可以使用  ，计算方法为：

                                                                      

实际上是P和R的加权调和平均数:           

这里的就是Recall的一个相对权重，越大，表示越注重R（召回率），时，表示更重视R召回率，时，表示更加重视P准确率。

1.6  AUC和ROC 

首先定义一下真正例率（TPR）和假正例率（FPR）：

                                                           

                                                           

TPR等价于召回率；TPR可以理解为正类样本中被预测为正类的比例，FPR可以理解为反类样本中被预测为正类的比例

我们希望模型的预测尽可能使得TPR搞，FPR低。跟PR曲线一样，我们将所有需要预测的样本排序，其中最有可能预测为正类的样本排在第一，最不可能的排在最后，在设定一个阈值，在阈值前面的样本我们都预测为正类，后面的预测为反类，如图（○表示正类，|表示阈值，×表示反类，下同）：

                                      ○○○○·····○○○○ | ×××××××·····×××××

然后我门通过不断调整阈值，得到很多组（TPR,FPR），以FPR为横轴，TPR为纵轴画图，得到ROC曲线。

① 假设所有样本都预测为正类：

                                                         ○○○○·····○○○○ | 

此时TPR = 1 （召回率，显然全部找到），FPR = 1 ，此时，对应图中点。

② 最后一个样本预测为反类，其余都为正类：

                                                         ○○○○·····○○○○ | ×

如果最后一个是反例，被预测为正例，则TPR不变，FPR上升（TN + 1），对应图中应该是点；如果最后一个是正例，被预测为反例，则TPR下降，FPR不变（FN + 1），对应图中应该是点。

③ 最后俩样本预测为反例，其余为正例：

                                                         ○○○○·····○○○ | ××

对应图中点。

               ······

最后，全部预测为反类：

                                                         | ××××·····×××××

这样子就画出了ROC曲线了，AUC就是ROC曲线下面部分的面积，就是图中的阴影部分：

样本量大时，折线段越来越光滑，ROC就变成一条曲线了。下面还是用西瓜书的图：

我们希望TPR尽量大于FPR，中间那条虚线就表示二者相等，表示模型的预测效果跟随机猜测是一样的。当TPR > FPR时，对应的点应该在图中虚线的上边部分，表示模型的预测效果比随机猜测准确性更高。相反，如果TPR < FPR,对应的点应该在图中虚线的下边部分，表示模型预测效果不如随机猜测。显然，ROC曲线越向上凸，模型性能越好。AUC是ROC曲线下方面积，AUC越大，也就是说曲线下面的面积越大，模型的分类效果越好。

补充一下：TPR可以理解为正类样本中被预测为正类的比例。FPR可以理解为反类样本中被预测为正类的比例。也就是说ROC曲线与样本中正负样本的比例无关，所以AUC曲线可以用于非均衡问题。

                                                           

2 回归问题的评价指标

2.1 MAE

MAE是指平均绝对误差（Mean Absolute Error），计算方法为：

                                                          

其中， 表示样本量,  表示样本标签， 表示样本的预测值，衡量预测值与真实值的偏差情况，一般情况下MAE越小越好。

优点：MAE可以理解为预测值与真实值的绝对距离的平均，相对于残差 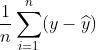   ，MAE不会因为残差的正负性而相互抵消。

缺点：因为加入绝对值，导致MAE损失函数不方便优化，例如在深度学习中，经常使用随机梯度下降法对参数进行优化，这就需要对损失函数进行求导，对MAE损失函数在某些点就不能求导。

2.2 MAPE

MAPE是指平均绝对百分误差（Mean Absolute Percentage Error），计算方法为：

                                                         

MAPE越小越好。这里需要注意一下不能为0.

2.3 MSE

MSE是指均方误差（Mean Square Error）,计算方法为：

                                                         

同MAE，MSE越小越好。解决了MAE（平均绝对误差无法求导的问题）

2.4 RMSE

MSE是指均方根误差（Root Mean Squared Error）,计算方法为：

                                                         

MSE的平方根，越小越好。

2.5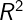 

是指决定系数（R-Square）,计算方法为：

                                                         

度量了因变量的变异中能够被自变量解释的比重，取值范围是 0-1 ，当 时，说明因变量完全由自变量决定，越大，模型的拟合效果越好。

还有一点需要注意的是， 相对于前面四个指标而言，是一个无量纲的指标，这给我们解决不同度量的问题带来很大方便。

3 参考

1 西瓜书

2 机器学习评估指标 - 知乎