机器学习、深度学习优化函数详解
机器学习、深度学习优化函数详解 – 潘登同学的Machine Learning笔记
文章目录
-
- 机器学习、深度学习优化函数详解 -- 潘登同学的Machine Learning笔记
- 简单回顾梯度下降法
-
- 随机梯度下降的不足
- 动量优化法(Momentum)
- Nesterov Momentum
- Adagrad优化法
- Adadelta优化法
- Adam优化法
- 图示各种优化方法
- 各种优化方法在Tensorlfow中的调用
-
- 梯度下降法
- Adagrad下降法
- 动量优化法
- RMSProp算法
- Adam算法
- Adadelta优化法
简单回顾梯度下降法
(算法)梯度下降法
Random 随机 θ \theta θ,随机一组数值 θ 0 , θ 1 , … , θ n \theta_0, \theta_1, \ldots, \theta_n θ0,θ1,…,θn
求梯度gradient
θ j t + 1 = θ j t − η ∙ g r a d i e n t j \theta_j^{t+1} = \theta_j^{t} - \eta \bullet gradient_j θjt+1=θjt−η∙gradientj
判断是否收敛 convergence,如果收敛跳出迭代,如果没有达到收敛,回第 2 步继续
能使用梯度下降法的一个最重要条件是:Loss函数是凸函数;更准确地说,想要用梯度下降去找到全局最小值,Loss必须是凸函数;
而现实中一般常用的是随机梯度下降SGD, 因为这有可能在非凸函数中找到最小值,而且在我们前面的代码实例中,也最常用SGD,下面来说说SGD的不足;
随机梯度下降的不足
- 很难选取一个适当的学习率。 选择的学习率太小,收敛速度慢;选择的学习率太高,参数波动太大,无法进入效果相对最优的点;
- 无法随着数据特点动态调整学习率,虽然可以在人工设置迭代第几轮时改变学习率,但是不能适合所有数据
- 所有特征共享相同的学习率,如果数据稀疏而且特征又特别大,可能训练到一个阶段时,部分参数需要较小的学习率,另一部分参数需要较大的学习率来调整
- 最重要的一点: 落入局部最小值,除了落入局部最小值外,还有可能陷入鞍点 (鞍点不是极小值点,鞍点就是一个导数为零的宽敞的平面,各个方向的梯度均为0)
动量优化法(Momentum)
- 思想:
基于动量的优化算法(Momentum),相当于在原来的更新参数的基础上增加了‘惯性的概念’;动量在梯度连续指向同一方向上时会增加,而在梯度方向变化时会减小。这样就可以更快收敛,并且减少振荡
(算法)动量优化法
Random 随机 θ \theta θ,随机一组数值 θ 0 , θ 1 , … , θ n \theta_0, \theta_1, \ldots, \theta_n θ0,θ1,…,θn
求梯度gradient
v j t + 1 = γ ∙ v j t + η ∙ g r a d i e n t j v_j^{t+1} = \gamma \bullet v_j^{t} + \eta \bullet gradient_j vjt+1=γ∙vjt+η∙gradientj
θ j t + 1 = θ j t − v j t + 1 \theta_j^{t+1} = \theta_j^{t} - v_j^{t+1} θjt+1=θjt−vjt+1
判断是否收敛 convergence,如果收敛跳出迭代,如果没有达到收敛,回第 2 步继续
注意 γ \gamma γ为动量更新值,一般取0.9
- 那还是没解决局部最小值问题呀?
基于动量优化法的特点,走到最小值的时候,更新的速率并不会马上变为0,因为还有前面累积下来的动量,所以动量优化法能从局部最小值中走出来;
- 冲出局部最小值的原因
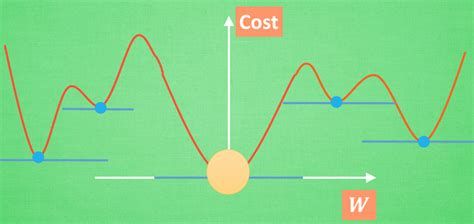
我们先看上图,假如初始随机化的参数是从最左边开始迭代的,因为最左边到第一个局部最小值的落差特别大,所以动量会非常大,可能冲过第一个局部最小值;
但是由于冲出第一个局部最小值后,需要经过一个山峰,这里会消耗很多动量,虽然过了山峰后仍会下降,但下降的动量仍不足以跨过第二个山峰;
因为第二个山峰还要比一开始的初始点要高,先别说动量更新值为0.9,就单单从动量守恒的角度都不能满足;
所以最终可能会落在第二个蓝色的点(也可能回到第一个蓝色的点),先别说第二个还不如第一个点呢,反正他是跨过了局部最小了;
Nesterov Momentum
Nesterov Momentum是对传统的Momentum方法的一项改进,

这个算法的基本思想是: 先按照原来更新方向更新一步,然后在该位置计算梯度,然后再用这个梯度修正最终的更新方向,上图中描述里两步的更新示意图,其中蓝色线是采用传统的Momentum的路径;也是启发式算法的一种,不仅局限于下一步,而且能多看一步
- 公式描述
先采用传统的Momentum
v j t + 1 = γ ∙ v j t + η ∙ g r a d i e n t j θ j t + 1 = θ j t − v j t + 1 v_j^{t+1} = \gamma \bullet v_j^{t} + \eta \bullet gradient_j\\ \theta_j^{t+1} = \theta_j^{t} - v_j^{t+1} \\ vjt+1=γ∙vjt+η∙gradientjθjt+1=θjt−vjt+1
再采用Nesterov Momentum( θ j t + 1 \theta_j^{t+1} θjt+1沿用上面的值)
v j t + 1 = γ ∙ v j t + η ∙ g r a d i e n t ( θ j t + 1 + γ ∙ v j t ) θ j t + 1 = θ j t − v j t + 1 v_j^{t+1} = \gamma \bullet v_j^{t} + \eta \bullet gradient(\theta_j^{t+1} + \gamma \bullet v_j^{t})\\ \theta_j^{t+1} = \theta_j^{t} - v_j^{t+1} \\ vjt+1=γ∙vjt+η∙gradient(θjt+1+γ∙vjt)θjt+1=θjt−vjt+1
Adagrad优化法
上面提到的动量优化算法对于所有参数都使用了同一个更新速率,但是同一个更新速率不一定适合所有参数。比如,有的参数可能已经到了仅需微调的阶段,但有些参数还需要较大幅度的调动。
- t时刻的学习率
η j t = η ∑ i = 1 t g i j 2 + ε \eta_j^t = \frac{\eta}{\sqrt{\sum_{i=1}^tg_{ij}^2+\varepsilon}} ηjt=∑i=1tgij2+εη
其中, g i j g_{ij} gij为第i时刻、第j个参数的梯度,而 ε \varepsilon ε是一个很小的数,只是为了确保分母非零;
这个公式的含义是,对于每个参数,随着其更新的总距离增多,其学习率也随之变慢。
Adagrad算法存在三个问题:
- 其学习率是单调递减的,训练后期学习率非常小
- 需要手工设置一个全局的初始学习率
- 学习率没有单位(因为导数也没有单位,所以学习率乘导数就没有单位,那么 △ θ \triangle \theta △θ就没有单位,但实际上 θ \theta θ是有单位的,因此前面的优化方法都有这个问题)
Adadelta优化法
ADADELTA: An Adaptive Learning Rate Method
Adadelta优化法对Adagrad算法的三个问题提出了更优的解决方案
- 第一个问题
解决方案:只Adagrad的分母中的累积项离当前时间点比较近的项
E [ g j 2 ] t = ρ E [ g j 2 ] t − 1 + ( 1 − ρ ) g t j 2 η j t = − η E [ g j 2 ] t + ε E[g_j^2]^t = \rho E[g_j^2]^{t-1} + (1-\rho)g_{tj}^2\\ \eta_j^t = -\frac{\eta}{\sqrt{E[g_j^2]^t+\varepsilon}} E[gj2]t=ρE[gj2]t−1+(1−ρ)gtj2ηjt=−E[gj2]t+εη
其中 ρ \rho ρ为衰减系数,通过衰减系数,能弱化之前梯度求和带来的学习率非常小的问题
- 解决第三个问题
解决方案:维护一个状态变量 △ θ \triangle \theta △θ
E [ △ θ j 2 ] t = ρ E [ △ θ j 2 ] t − 1 + ( 1 − ρ ) △ θ t j 2 η j t = − E [ △ θ j 2 ] t − 1 E [ g j 2 ] t + ε E[\triangle \theta_j^2]^t = \rho E[\triangle \theta_j^2]^{t-1} + (1-\rho)\triangle \theta_{tj}^2\\ \eta_j^t = -\frac{\sqrt{E[\triangle \theta_j^2]^{t-1}}}{\sqrt{E[g_j^2]^t+\varepsilon}} E[△θj2]t=ρE[△θj2]t−1+(1−ρ)△θtj2ηjt=−E[gj2]t+εE[△θj2]t−1
这样修正之后,学习率就自然带上了 θ \theta θ的单位;
同时,也把初始的 η \eta η消去了,也顺带解决了第二个问题;
上面的这个公式是模拟牛顿法迭代法(就是把一阶导换成二阶导的那个优化方法,在决策树章节有相关介绍)
η j t = − 1 ∣ d i a g ( H t ) ∣ ( E [ g j ] t ) 2 E [ g j 2 ] t + ε \eta_j^t = -\frac{1}{|diag(H^t)|}\frac{(E[g_j]^{t})^2}{E[g_j^2]^t+\varepsilon} ηjt=−∣diag(Ht)∣1E[gj2]t+ε(E[gj]t)2
其中, ∣ d i a g ( H t ) ∣ |diag(H^t)| ∣diag(Ht)∣表示的是第t时刻的海塞矩阵对角化后的行列式
注意 而另外一个常用的RMSprop算法就是只解决第一个问题的Adadelta算法,RMSProp算法在经验上已经被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习从业者经常采用的优化方法之一
Adam优化法
Adam全称是: 自适应矩估计(Adaptive Moment Estimation)
Adam是融合了SGD的两个改进方向的优化器(一个是动态调整学习率,一个是保存动量)。
-
Adam中维护了两个状态变量 m t 、 v t m^t、v_t mt、vt
m j t = β 1 m j t − 1 + ( 1 − β 1 ) g j t v j t = β 2 v j t − 1 + ( 1 − β 2 ) ( g j t ) 2 m_j^t = \beta_1 m_j^{t-1} + (1-\beta_1)g_j^t\\ v_j^t = \beta_2 v_j^{t-1} + (1-\beta_2)(g_j^t)^2\\ mjt=β1mjt−1+(1−β1)gjtvjt=β2vjt−1+(1−β2)(gjt)2 -
一阶距与二阶矩的偏差修正
m ^ j t = m j 1 − ( β 1 ) t v ^ j t = v j 1 − ( β 2 ) t \hat{m}_j^t = \frac{m_j}{1-(\beta_1)^t}\\ \hat{v}_j^t = \frac{v_j}{1-(\beta_2)^t}\\ m^jt=1−(β1)tmjv^jt=1−(β2)tvj -
自适应的学习率
η = α m ^ j t v ^ j t + ε \eta = \alpha\frac{\hat{m}_j^t}{\sqrt{\hat{v}_j^t}+\varepsilon} η=αv^jt+εm^jt
一般默认的 β 1 = 0.9 , β 2 = 0.999 , ε = 1 0 − 8 , α = 0.001 \beta_1=0.9,\beta_2=0.999,\varepsilon=10^{-8},\alpha=0.001 β1=0.9,β2=0.999,ε=10−8,α=0.001
图示各种优化方法
各种优化方法在Tensorlfow中的调用
梯度下降法
learning_rate = 0.001
tf.train.GradientDescentOptimizer(learning_rate, use_locking=False, name='GradientDescent')
其中, use_locking为True时锁定更新
Adagrad下降法
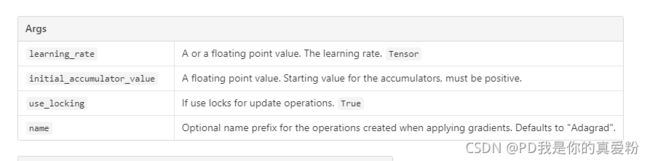
tf.train.AdagradOptimizer(learning_rate, initial_accumulator_value=0.1, use_locking=False,name='Adagrad')
其中, initial_accumulator_value为累加器的系数,我认为应该就是前面
η j t = η ∑ i = 1 t g i j 2 + ε \eta_j^t = \frac{\eta}{\sqrt{\sum_{i=1}^tg_{ij}^2+\varepsilon}} ηjt=∑i=1tgij2+εη
的 g i j 2 g_{ij}^2 gij2前的系数,如果是1的话,就跟我们的算法一致;所以我猜测就是一个能改进算法的系数,与后面的RMSprop算法求指数化平均的意思差不多。
动量优化法
momentum = 0.9
tf.train.MomentumOptimizer(learning_rate, momentum, use_locking=False, name='Momentum', use_nesterov=False)
其中, momentum为 γ \gamma γ,一般设置为0.9; use_nesterov=True,表示该优化器实现牛顿加速梯度(NAG, Nesterov accelerated gradient)算法,该算法是Momentum动量算法的变种。
RMSProp算法
tf.train.RMSPropOptimizer(learning_rate, decay=0.9, momentum=0.0, epsilon=1e-10, use_locking=False, name='RMSProp')
其中, decay为 ρ \rho ρ; epsilon为 ϵ \epsilon ϵ,一般为 e − 10 e^{-10} e−10
Adam算法
tf.train.AdamOptimizer(learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08, use_locking=False, name='Adam')
其中,beta1=0.9, beta2=0.999, epsilon=1e-08就是算法中 β 1 , β 2 , ϵ \beta_1,\beta_2,\epsilon β1,β2,ϵ的含义,较优的参数就是0.9,0.999,1e-08; 而这里的learning_rate=0.001其实是算法中的 α \alpha α, 虽然表述上不一样,但就是用一个系数去乘上学习率,理解为学习率也没啥毛病;
Adadelta优化法
tf.train.AdadeltaOptimizer(
learning_rate=0.001, rho=0.95, epsilon=1e-08, use_locking=False, name='Adadelta')
其中, rho为 ρ \rho ρ; epsilon为 ϵ \epsilon ϵ,一般为 e − 10 e^{-10} e−10
机器学习、深度学习优化函数详解就是这样了, 继续下一章吧!pd的Machine Learning