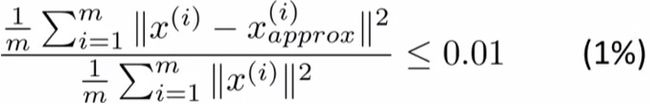维数约减--Dimensionality Reduction
维数约减属于无监督学习范畴，我们希望使用维数约减的原因可能有：通过数据压缩以减少数据占有内存的大小，为算法运算提高速度，将数据可视化等。
数据压缩-data compression
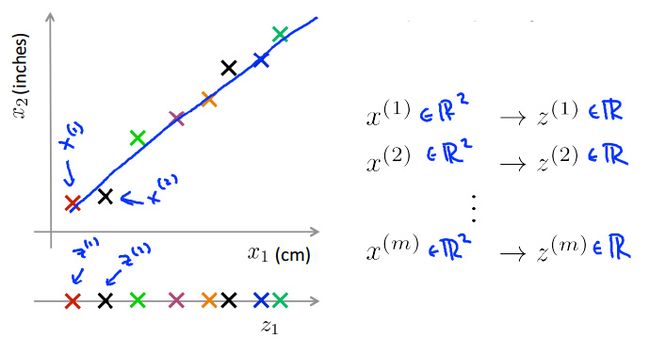
某个物体的长度以x1厘米为单位，另一个x2是它以英寸为单位的长度。这是一个非常冗余的数据，所以与其用两个特征变量x1和x2，但它们都是测量到的长度，或许我们应该把这个数据降到一维，这样一来只用一个长度的数据。
从二维/2D降到一维/1D到底意味着什么？通过样本涂上不同的颜色，在这个例子中降低维度的意思指找到这样一条线，基本所有点都落在这个方向上然后把所有的数据映射到这条线上，这样做之后就可以直接测量这条线上每个样本的位置，现在把这个新特征叫做z1，要确定这条线上的位置只需要一个数字，这就是说新特征变量z1能够表示这条绿线上每一个点的位置。
更具体地，之前我们有一个样本x(1)，比如这是第一个样本x(1)，为了表示原本的x(1)，需要一个二维数字或者一个二维特征向量，但是现在可以只用z(1)来表示第一个样本x(1)，以此类推到m个样本上。
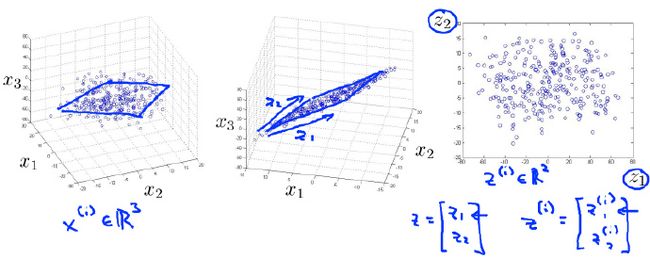
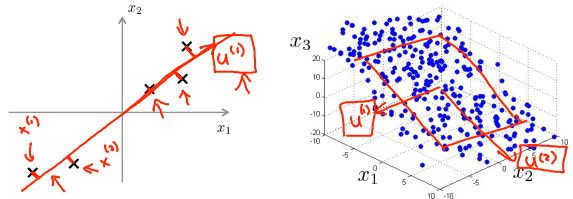
接着举一个3D缩减为2D的例子，如下：左边是原始数据集，中间是投影到2D的数据集，右边是以z1和z2为坐标轴的2D数据集。我们来更详细地看一下左侧，这是原始数据集（3D点云），开始它的坐标轴是x1,x2,x3。所以这是一个3D的点云，但是大部分数据都落在某个2D平面上或者说距离某个2D平面不远。
接着如中间的图片一样，把它们投影到2D平面，现在只需要两个数z1和z2来表示点在平面上的位置，如右侧的图像，这就是把数据从三维降到二维的过程降到二维的过程，这就是维数约减以及如何使用它来压缩数据。
可视化数据-data visualization
除了压缩数据，可视化数据对于机器学习的应用帮助也很大，可以提高开发高效学习算法的效率，而前提要求我们必须很好地理解数据。
假如我们收集了大量的关于全世界不同国家的统计数据集，第一个特征x1是国内生产总值，x2是每人占有的GDP，x3人类发展指数，x4预期寿命，x5x6等。像这里这样的数据对于每个国家可能有50个特征，我们有这样的众多国家的数据集，那么有没有办法使得我们能更好地来理解数据？
这里给出了一张有数字的表格，你怎样将这些数据可视化？如果有50个特征绘制一幅50维度的图是异常困难的，那有没有观察数据的好办法呢？
降维
我们使用特征向量x(i)来表示每个国家，x(i)有着50个维度。例如，加拿大这个国家的特征用50个数字来代表，我们要能提出一种不同的特征表示方法，使用一个二维的向量z来代替x。
在这种情况下我们可以使用一对数字z1和z2，从某种程度来说这两个数总结了50个数，也许我们可以使用这两个数来绘制出这些国家的二维图。使用这样的方法尝试去理解二维空间下不同国家在不同特征的差异更容易。所以，这里将数据降维从50维度降维到2维度，这样就可以绘制出2D的图像。
仔细观察降维算法的输出结果，它通常不能赋予你想要的这些二维新特征一个物理含义，在这里每个国家用一个点z(i)表示，z(i)是一个二维数据，或许会发现例如那条水平轴即z1轴大致对应了国家总面积或者一个国家的总体经济活动情况，然而纵轴即z2的数据或许对应着人均GDP或是人均幸福感。
可以发现对于50个特征，到最后主要是这2个维度的特征来进行表示。上图中，像美国有着相当大的总GDP以及相对的高人均GDP，像新加坡这样的国家生产总值并不算高，但人均幸福度很高。
主成分分析法-Principal Component Analysis（PCA)
公式formula
对于降维问题，目前最流行的算法是主成分分析法PCA，首先我们用公式准确的描述想让PCA来做什么。我们有这样的一个数据集，这个数据集含有二维实数空间内的样本X，假设我想对数据进行降维，即从二维降到一维，现在想找到一条直线将数据投影到这条直线上那怎么找到一条好的直线来投影这些数据呢？
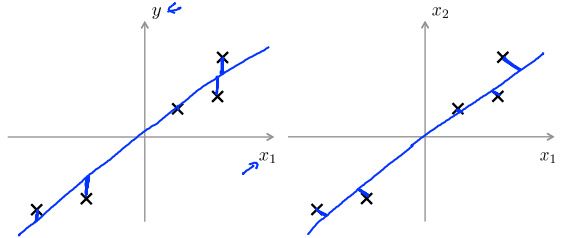
下图这样的一条直线也许是个不错的选择，因为每个点到它们对应的投影到直线上的点之间的距离非常小，也就是说这些蓝色的线段非常的短。
正式的讲，PCA所做的就是寻找一个低维的面（在这个例子中其实是一条直线），数据投射在上面使得这些蓝色小线段的平方和达到最小值，这些蓝色线段的长度时常被叫做投影误差。所以PCA所做的就是寻找一个投影平面对数据进行投影使得这个能够最小化。
更一般的情况是我们有n维的数据想降到k维，在这种情况下我们不仅仅只寻找单个的向量来对数据进行投影我们要找到k个方向来对数据进行投影从而最小化投影误差。
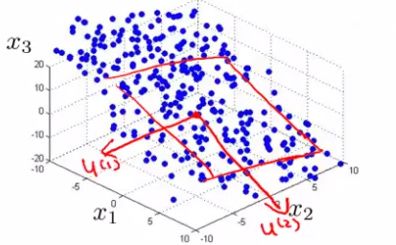
如果有下图所示的一些三维数据点，那么我们想要做的是寻找两个向量，用红线画出来， 寻找两个向量从原点延伸出来，这是u(1)这是第二个向量u(2)，这两个向量一起定义了一个平面或者说定义了一个二维面。因此PCA做的就是寻找一条直线或者平面诸如此类等等对数据进行投影来最小化平方投影90度的或者正交的投影误差。
PCA 并不是线性回归
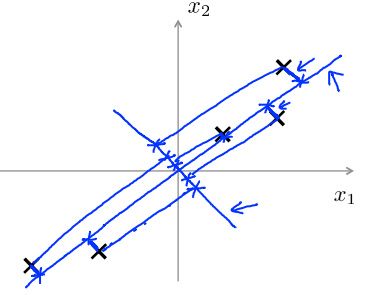
尽管看上去有一些相似但是它们确实是两种不同的算法，如下图左侧，要在给定某个输入特征x的情况下预测某个变量y的数值，故对于线性回归我们想做的是拟合一条直线来最小化点和直线之间的平方误差。所以我们要最小化的是这些蓝线幅值的平方，注意所画的这些蓝色的垂直线，这是垂直距离，它是某个点与通过假设的得到的其预测值之间的y轴方向上的距离。
与此想反，如上图右侧，PCA要做的是最小化这些蓝色直线的幅值，这实际上是最短的直角距离，也就是点x跟直线之间的最短距离。
更一般的是当你做线性回归的时候有一个特别的变量y，我们将要预测的线性回归就是用x的所有的值来预测y。然而，在PCA中没有这么一个特别的或者特殊的变量y，我们所拥有的是特征x1，x2等一直到xn所有的这些特征都是被同样地对待因此它们中没有一个是特殊的。
PCA算法实现
在使用PCA之前我们通常会有一个数据预处理的过程：拿到某组有m个无标签样本的训练集一般先进行均值归一化(meannormalization)，这一步很重要，然后还可以进行特征缩放(featurescaling)这根据你的数据而定。这跟我们之前在监督学习中提到的均值归一和特征缩放是一样的实际上它们是完全一样的步骤只不过现在我们针对的是一系列无标签的数据x(1)到x(m)，因此对于均值归一我们首先应该计算出每个特征的均值μ，然后我们用x-μ来替换掉x这样就使得所有特征的均值为0。
由于不同特征的取值范围都很不一样，比如说如果x1表示房子的面积，x2表示房屋的卧室数量。然后我们可以把每个特征进行缩放，使其处于同一可比的范围内。
同样地，跟之前的监督学习类似我们可以用xj(i)xj(i)减去平均值μj，除以sj来替换掉第j个特征xj(i)xj(i)，这里的sj表示特征j的某个量度范围，因此它可以表示最大值减最小值，更普遍地，它可以表示特征j的标准差进行。
完以上这些数据预处理后接下来就正式进入PCA的算法部分。在上节中我们已经知道了PCA的原理，PCA是在试图找到一个低维的子空间，然后把原数据投影到子空间上并且最小化平方投影误差的值，或者说投影误差的平方和。因此我们想要做的是找到某个具体的向量u(1)指定这条投影线的方向，或者在2D的情况下我们想要找到两个向量u(1)和u(2)来定义一个投影平面对数据进行投影。
PCA要做的事儿就是要得到一种方法来计算两个东西，其一是计算这些向量比如这里的u(1)，这里的u(1)、u(2)。另一个问题是怎样计算出这些z，对于左边这个例子我们要把数据从二维降到一维，对于右边这个例子我们要把数据从三维降到二维。从原来的x(i)变为现在的z(i)，新的z向量是二维的，它应该是{z1，z2}这样的一个向量。
因此我们需要找到某种办法来算出这些新的变量也就是z1和z2，那么应该怎样来计算这些值呢 ?
假如说我们想要把数据从n维降低到k维，我们首先要做的是计算出这个协方差矩阵（covariance matrix）通常以希腊字母大写的∑来表示，这里区分与后面的求和符号，假如我们把协方差矩阵存为Octave/MATLAB中的一个变量叫Sigma，我们需要做的是计算出Sigma矩阵的特征向量(eigenvectors)。
在Octave/MATLAB中你可以使用如下命令来实现这一功能
[U,S,V]=svd(Sigma); svd表示奇异值分解(singular value decomposition)，这是某种更高级的奇异值分解，此外还有另一个eig命令，也可以用来计算特征向量。参见强大的矩阵奇异值的分解SVD应用
实际上svd命令和eig命令将得到相同的结果，这是因为协方差均值总满足一个数学性质--对称正定(symmetric positive definite)，但是svd其实要更稳定一些。
协方差矩阵Sigma应该是一个n×n的矩阵，然后svd将输出三个矩阵分别是U、S、V。这里真正需要的是U矩阵，U矩阵也是一个n×n矩阵。如果我们想将数据的维度从n降低到k的话，我们只需要提取前k列向量，这样我们就得到了u(1)到u(k)，也就是我们用来投影数据的k个方向。
接下来对于原始数据集x，x是一个n维实数，然后我们要找到一个低维的表达z，z是k维实数，我们构建这样一个矩阵把u(1)、u(2)一直到u(k)，并列地合起来，其实就是取出这个U矩阵的前k列元素，将这个新的矩阵成为UreduceUreduce即约减后的矩阵。z等于这个UreduceUreduce矩阵的转置乘以x。
小结一下：首先对数据集进行预处理，利用均值归一化确保所有的特征均值为零，必要时可以添加特征缩减，接着计算协方差矩阵sigma∑，为：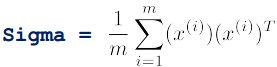
，利用octave/Matlab中的奇异值分解svd函数得到约减矩阵：
[U,S,V] = svd(Sigma);
Ureduce = U(:,1:k); 计算投影值：z = Ureduce'*x;
重构--将压缩过的数据还原-Reconstruction
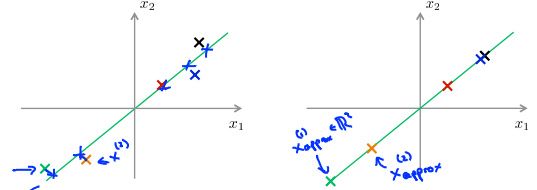
如下图：现有样本x(1)样本x(2)，那我们要让这些样本投影在一维平面上，我们现在只需要使用一个实数就能在它们全部被投影到这个一维平面z1上，并且明确地指定其位置。
反过来，任意给一个点比如这个点z(1)，如何重新得到原来的二维数据点呢？具体来说就是给出一个一维实数点z，我们能否让z重新变成原来的二维实数点x？我们知道z的值等于U_reduce的转置乘以x，如果想得到相反的情形方程应这样变化x_approx应该等于U_reduce乘以z为了检查维度，这里U_reduce是一个n×k矩阵，z就是一个k×1维向量，将它们相乘得到的就是n×1维。所以说x_approx是一个n维向量，同时根据PCA的意图：投影的平方误差不能很大，也就是说x_approx将会与最开始用来导出z的原始x很接近。
用图表示出来，我们可以看到这些点都到绿线上去了，与原始样本点的位置有一定误差，但已经是与原始数据非常近似了，通过这个公式我们得到x_approx(1)对应于图上x_approx(1)，可以使用同样的步骤计算出x_approx(2)。
这就是用低维度的特征数据z回到未被压缩的特征数据，我们找到一个与原始数据x近似的x_apporx我们也称这一过程为原始数据的 重构 (reconstruction)，我们可以在需要从压缩过的数据重构出原始数据x时使用这种方法。
确定k值
在正式确定中心成分的数目k值时，我们需要先了解俩个定义，第一：平均平方映射误差(Average Squared Projection Error)，它是原始数据x和映射值x_approx(i)之间的差，PCA就是要将这个量最小化。这个在上节中也做过定义，它就是要最小化x和其在低维表面上的映射点之间的距离的平方。
1m∑mi=1||x(i)−x(i)approx||21m∑i=1m||x(i)−xapprox(i)||2
第二：数据的总变差(TotalVariation)，它是这些样本x(i)的长度的平方的均值，意思是“平均来看训练样本距离零向量（零点）距离。
1m∑mi=1||x(i)||21m∑i=1m||x(i)||2
一个非常常用的选择k值的方法是希望平均平方映射误差就是x和其映射值之间的平均距离，除以数据的总变差，希望这个比值能够小于0.01或者说是小于1%。
因此如果你使用PCA，并且你想要告诉别人你保留了多少个主成分，更为常见的一种说法是，选择了参数k使得99%的差异性得以保留，此外人们经常用的另一个常用的值是0.05，那么这就会是5%如果是这样的话你可以说95%的差异性被保留了。
对于选取k的值，最容易想到的：我们可以从k=1开始，然后我们再进行主成分分析我们算出U_reduce，z(1)、z(2)一直到z(m)。算出所有x_approx(1)一直到x_approx(m)，然后看99%（或90%）的差异性是否被保留下来了，如果不是接下来尝试k=2，然后重新走一遍整个过程检查是否满足这个表达式，如果不是我们再重复一次我们尝试k=3然后试k=4，以此类推一直试到比如我们一直试到k=17然后发现99%的数据都被保留了。我们就会用k=17这是一种用来选择使得99%的差异性能够得以保留的最小的k值的方法，但是可以想见这个过程的效率相当地低！！
其实在应用PCA时，它已经给了我们一个可以使计算变得容易很多的量，特别是当你对协方差的矩阵Sigma调用svd时，我们还会得到这个矩阵S，S是一个正方形矩阵实际上是一个n×n的矩阵，它是一个对角矩阵对角线上的元素是s11,s22,s33s11,s22,s33一直到snnsnn。
假如说k=3，我们接下来要计算的分子是从i=1到3对Sii求和从i=1到3对Sii求和就是算出这前三个元素的和，这就是分子。然后计算分母分母是这些对角元素的总和。
你要做的就是慢慢地增大k值，把k值设为1、k值设为2、把k值设为3，以此类推并检验这个数值。找出能够确保99%的差异性被保留的最小的k值，找出能够确保99%的差异性被保留的最小的k值。
如果这样做，只需要调用一次svd函数，因为它会给你S矩阵，一旦有了S矩阵便可以通过增加分子上的k值，通过增加分子上的k值来做这个计算，因此就不用一遍一遍地调用svd函数来检验不同的k值。
顺便说一下，如果想要向他们解释你实现的PCA的性能的一个好方法实际上是这个数值把它算出来，它会告诉你百分之多少的差异性被保留了下来，如果你把这个数值展现出来，那么熟悉PCA的人们就可以通过它来更好地理解你用来代表原始数据的100维数据近似得有多好。
PCA应用中的几点建议
首先介绍如何通过PCA来提高学习算法的速度，比如说你遇到了一个监督学习问题注意这个监督学习算法问题有输入x和标签y，而你的样本x(i)是非常高维的数据，比如说x(i)是一个10,000维的向量，如一张100×100的图片。如果x(i)是包含了这10000像素强度值的特征向量，那么就会有10000维特征向量。
如果你输入10,000维的特征向量到逻辑回归中或者到一个神经网络、支持向量机中，或是任何别的算法中，像这样有很高维的特征向量运行会比较慢。使用PCA能够降低数据的维数从而使算法更加高效地运行。
提取出x并暂时把y放在一边，通过这一步会得到一组无标签的训练集，从x(1)到x(m)这可能会有10,000维数据也就是10,000维数据样本所以就是从数据组中x(1)到x(m)中提取出输入向量。
接着应用PCA，会得到一个降维的数据，与刚才的10,000维特征相比，现在就只有1000维特征向量，因此这就降低了10倍。新的训练集样本用z(1)来表示，其中z(1)与y(1)是一对儿，同样地，z(2)对应y(2)等等，一直到z(m)对y(m)，因为现在的训练集由这样一个更加低维的数据集所代替z(1),z(2)一直到z(m)。最后将这个已经降维的数据集输入到学习算法或者是将其放入到神经网络中，学习出假设h把这些低维的z作为输入并作出预测。
最后要注意一点PCA定义了从x到z的对应关系，这种从x到z的对应关系只可以通过在训练集上运行PCA定义出来。
具体来讲，计算出这样一个降维的矩阵U_reduce，但是降维矩阵U_reduce中的数据就像一个PCA所学习的参数一样，我们需要使参数唯一地适应这些训练集而不是适应交叉验证或者测试集。
因此U_reduce矩阵中的数据应该只通过对训练集运行PCA来获得，找出了降维矩阵U_reduce或者找出了这些特征扩展的参数之后，均值均一化，在训练集中找到了所有这些参数后就可以将同样的对应关系应用到其他样本中了可能是交叉验证数集样本或者测试数据集中。
总结一下，当在运行PCA的时候只是在训练集那一部分来进行的而不是交叉验证的数据集，这就定义了从x到z的映射，然后就可以将这个映射应用到交叉验证数据集中和测试数据集中。
假设x(i)为有n个特征的数据集，我们将数据进行压缩并用压缩后的数据z(i)来代替原始数据，在降维过程中我们从n个特征降维到k个，比先前的维度低。例如如果我们有非常小的特征数目，假如k值为1000，n值为10000，那么1000维度的数据和用10000维度的数据比起来对于同样是1000个特征来说或许更不容易过拟合。所以有些人认为PCA是一种避免过拟合的方法，然而这并不是一个合适的PCA应用。仔细想想PCA是如何工作的它并不需要使用数据的标签label，只需要输入数据x(i)，同时使用这个方法时PCA把某些信息舍弃掉了。而只使用正则化将会是一种避免过拟合绝对好的方法。
建议一开始不要将PCA方法就直接放到算法里，先使用原始数据x(i)看看效果，只有一个原因让我们相信算法出现了问题那就是你的学习算法收敛地非常缓慢占用内存或者硬盘空间非常大，所以你想来压缩数据只有当你的x(i)效果不好只有当你有证据或者充足的理由来确定x(i)效果不好的时候那么就考虑用PCA来进行压缩数据。