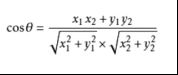Python 实现三维姿态估计遮挡匹配预测

作者 | 李秋键

出品 | AI科技大本营（ID:rgznai100）

引言：随着计算机技术的飞速发展以及人们对智能化设备需求的提高，人体行为识别已经成为计算机视觉领域热门研究方向之一，其广泛应用于公共安防、人机交互、虚拟现实、体育运动和医疗健康等领域，具有极高的理论研究价值。早期的方法主要针对于 RGB 视频图像，由于易受复杂背景、光照强度的影响，很难达到理想效果。但随着深度传感器技术的发展，高精度获取三维骨架关节点信息变得方便可行。对比传统 RGB 视频图像数据，骨架姿势信息对行为的描述有其内在优势，它不仅能够更准确地描述人体姿态和运动状态而且不受背景复杂度及光照强度等因素的影响，同时骨架信息也可以被广泛应用于行为识别。

三维人体姿态估计的主要任务是预测出人体关节点的三维坐标位置和角度等信息。其对于人体姿态的表述比2D更为精准，因此其应用范围和参考价值都要高于2D人体姿态估计，但是3D姿态估计的难度也更高，存在着遮挡，单视角2D到3D的映射中固有的深度模糊性、不适定性，缺少大型的室外数据集等挑战。

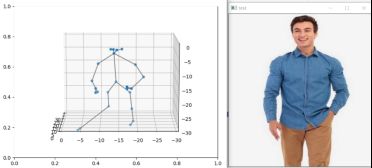
故今天我们尝试在获取三维姿态估计骨骼数据的基础上，对其缺少的数据进行匹配性的预测，参考GCN等构建空间结构算法可能更优，但这里只作为一种方法的思路，其他方法后续补充，效果如下，代码放置文末，大家可以优化： 

方法基本介绍

1.1 余弦相似度

余弦相似度，又称为余弦相似性，是通过计算两个向量的夹角余弦值来评估他们的相似度。余弦相似度将向量根据坐标值，绘制到向量空间中，如最常见的二维空间。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似。余弦相似度计算源于向量余弦计算的思想，通过测量两个向量内积空间夹角的余弦值来度量它们之间的相似性，常用于机器学习中对文本的处理过程。计算两段文本的相似度首先需要将文本分词，清除标点符号以及停用词，对文本中涉及的词进行统一数字编码，根据编码将文本中的词频向量化，再用余弦定理计算两个向量的余弦值，即可得到两段文本的相似度。

1.2 皮尔逊系数

皮尔逊相关系数是一种广泛用于测量两个变量之间线性相关性的方法。它基于数据的协方差矩阵来评估两个向量之间关系的强度。通常，两个向量之间的皮尔逊相关系数为：

皮尔逊相关系数可以应用于样本或总体。样本和总体的皮尔逊相关系数的绝对值均小于或等于 1。在样本相关的情况下，相关系数等于 1 或-1 对应于恰好位于一条线上的数据点；在总体相关的情况下，这对应于一条完全支持双变量分布的线。

1.3 匹配方法介绍

本文所采用的方法和图像模板匹配基本类似，这里做基本介绍。

图像模板匹配方法可以分成四种类型：基于图像灰度的图像匹配算法、基于变换域的图像匹配算法、基于模板的图像匹配算法和给予特征的图像匹配算法。基于特征的匹配算法通过提取图像中对形变、光照等具有不变性的信息，对这些信息进行描述构造描述符，之后对这些特征进行匹配，计算出图像之间几何变换的参数。基于特征的匹配算法比起基于灰度的匹配算法是用更少的信息进行匹配，从而大大提高运算速度。

基于特征的匹配算法主要包括特征提取、特征匹配、生成几何变换这几个步骤。特征提取是指提取出图像中具有代表性的信息，例如：图像中的角点、拐点等，提取出来的信息必须满足对尺度、旋转、光照、视角和噪声干扰等影响因素具有一定程度的鲁棒性。除此之外所提取的特征还必须具有独特性，以防止将相似的特征被误认为是相同的事物，从而造成特征的误配

项目搭建

这里首先介绍下基本思路，首先需要构建匹配数据集，然后提取骨骼保存为模型文件，然后使用匹配方法找到匹配点预测补充即可。故可分为以下几个步骤进行：

2.1 匹配模型构建

首先要准备数据集如下图可见，可以自行添加更多数据：

然后构建提取模型，保存为npy文件。部分代码如下：

if np.max(joint_heat)>0.1:
        [x, y, z] = np.where(joint_heat == np.max(joint_heat))
        x = int(x[-1])
        y = int(y[-1])
        z = int(z[-1])
        pos_x = offset3D[j * 28 + x, y, z] + x
        pos_y = offset3D[24 * 28 + j * 28 + x, y, z] + y
        pos_z = offset3D[24 * 28 * 2 + j * 28 + x, y, z] + z
        kps[j, 0] = pos_x
        kps[j, 1] = pos_y
        kps[j, 2] = pos_z
        positions.append([pos_x, pos_y, pos_z])
    else:
        [x, y, z] = np.where(joint_heat == np.max(joint_heat))
        x = int(x[-1])
        y = int(y[-1])
        z = int(z[-1])
        pos_x = offset3D[j * 28 + x, y, z] + x
        pos_y = offset3D[24 * 28 + j * 28 + x, y, z] + y
        pos_z = offset3D[24 * 28 * 2 + j * 28 + x, y, z] + z
        kps[j, 0] = pos_x
        kps[j, 1] = pos_y
        kps[j, 2] = pos_z
        positions.append([pos_x, pos_y, pos_z])
positions=np.array(positions)
data = np.vstack((data, positions))
np.save('data.npy', data)

2.2 遮挡匹配估计

这里主要测试了余弦相似度匹配和皮尔逊系数进行匹配，核心代码如下：

if np.max(joint_heat)>0.1:
    [x, y, z] = np.where(joint_heat == np.max(joint_heat))
    x = int(x[-1])
    y = int(y[-1])
    z = int(z[-1])
    pos_x = offset3D[j * 28 + x, y, z] + x
    pos_y = offset3D[24 * 28 + j * 28 + x, y, z] + y
    pos_z = offset3D[24 * 28 * 2 + j * 28 + x, y, z] + z
    kps[j, 0] = pos_x
    kps[j, 1] = pos_y
    kps[j, 2] = pos_z
    positions.append([pos_x, pos_y, pos_z])
else:
    tmp = sum(positions, [])
    lens = len(tmp)
    idx=0
    max_similar = float('-inf')
    min_similar=float('inf')
    for i in range(1,len(res)):
        arr = list(np.concatenate(res[i].reshape((-1, 1), order="F")))[:lens]
        '''1 余弦相似度'''
        s = cosine_similarity([arr], [tmp])
        print(s)
        if s >= max_similar:
            max_similar = s
            idx = i
        '''2、皮尔逊系数'''
        # s = pearsonrSim(arr, tmp)
        # print(s)
        # if s < min_similar:
        #     min_similar = s
        #     idx = i
    print((res[idx][lens//3][1]-res[idx][lens//3-1][1]))
    pos_x = positions[-1][0]+(res[idx][lens//3][0]-res[idx][lens//3-1][0])
    pos_y = positions[-1][1]+(res[idx][lens//3][1]-res[idx][lens//3-1][1])
    pos_z = positions[-1][2]+(res[idx][lens//3][2]-res[idx][lens//3-1][2])
    kps[j, 0] = pos_x
    kps[j, 1] = pos_y
    kps[j, 2] = pos_z
    print(idx)
    positions.append([pos_x, pos_y, pos_z])

完整代码：

链接：https://pan.baidu.com/s/1DmGasSN219rrFORdy300Tw

提取码：jjy1

李秋键，CSDN博客专家，CSDN达人课作者。硕士在读于中国矿业大学，开发有taptap竞赛获奖等。