第十三届蓝桥杯青少组省赛C++中级组(0423)
选择题(单选)
选择题1:20分
下列关于类中声明的变量描述正确的是(D)。
A.只属于该类
B.属于全局变量
C.任何情况下都可被该类所有实例共享
D.属于该类,某些情况下也可被该类不同实例所共享
选择题2:20分
下列对抽象类描述正确的是(D)。
A.抽象类没有构造方法
B.抽象类必须提供抽象方法
C.抽象类可以通过new关键字直接实例化
D.有抽象方法的类一定是抽象类
选择题3:20分
二进制减法11101101-11001001(C)。
A.10111011
B.11001001
C.100100
D.10101111
选择题4:20分
以下数据结构中,能够按照“先进后出”原则存取数据的是(A)。
A.栈 B.队列 C.二又树 D.循环队列
选择题5:20分
下列对int *p[3]描述正确的是(B)。
A.p[3]表示数组的第3个元素的值,是int类型的值
B.p是一个具有3个元素的指针数组,每个元素是一个int 类型指针
C.p是一个指向数组的指针,所指向的数组是3个int 类型元素
D.p是一个指向某数组中第3个元素的指针,该元素是int 型变量
编程题1:统计数字(30分)
题目描述:
给定一个正整数N,找出3到N之间的正整数中,个位数为3的有多少个。
例如:N=25,3至25之间个位数为3的有3、13、23,一共有3个。
输入描述:
输入一个正整数N(3≤N≤99993)输出描述:
输出一个整数,表示3到N之间的正整数中,个位数为3的个数(包括3和N)
样例输入:
25
样例输出:
3
#include
#include
using namespace std;
int main()
{
int n,ans=0;
cin>>n;
for(int i=3;i<=n;i++){
if(i%10==3)
ans++;
}
cout< 编程题2:字母组合(40分)
题目描述:
给定N个小写字母,然后将N个小写字母按照字典排序后组合成一个字符串并输出。
例如N=4,4个小写字母分别为c,d,a,c,按照字典排序后组合成的字符串为:accd
输入描述:
第一行输入一个正整数N(2
输出描述:
将N个小写字母按照字典排序后组合成一个字符串并输出
样例输入:
4
c d a c
样例输出:
accd
#include
#include
#include
using namespace std;
char a[105];
int main()
{
int n;
cin>>n;
for(int i=0;i>a[i];
sort(a,a+n);
cout< 编程题3:组合(50分)
题目描述:
某商家将一种汤圆按照数量不同,分装成N种规格来售卖。这样的售卖方式会限制一些数量的汤圆不能买到。
例如:
N=2,2种规格的汤圆分别装3个和5个,这种情况下限制了1,2,4,7四种数量的汤圆不能买到。
给出N及N种规格的汤圆数量,请计算出有多少种数量的汤圆不能买到,如果有无限种数量的汤圆不能买到就输出“-1”。
输入描述:
第一行输入一个正整数N(1
输出描述:
输出在这种情况下有多少种汤圆数量是不能买到的,如果有无限种数量的汤圆不能买到就输出“-1”
样例输入:
2
3 5
样例输出:
4
#include
#include
#include
using namespace std;
int n,a[25],f[10005],g;
int gcd(int a,int b){
if (a%b==0) return b;
else return gcd(b,a%b);
}
int main()
{
cin>>n>>a[0];
g=a[0];
f[a[0]]=1;
for(int i=1;i>a[i];
g=gcd(g,a[i]);
f[a[i]]=1;//标记a[i]能被取到
}
//n个数字如果不能互质
//则不能组合的数字有无限个
if(g!=1){
cout<<-1< 编题4:帮助(60分)
题目描述:
已知有M名需要帮助的贫困学生,及每名学生购买图书的金额;和N位愿意提供帮助的志愿者,及每名志愿者愿意帮助的金额。
现N名志愿者认领贫困生进行帮助,每人可以认领贫困学生的名额不限,但如果志愿者愿意帮助的金额小于每名贫困生购买图书的金额,那么该志愿者不能认领贫困学生。请你计算出这些志愿者最多可以认领多少名贫困学生(一名学生只能被一名志愿者认领)。
例如:M=5,N=2
5名贫困学生购买图书金额分别是:200、145、240、50、45,2名志愿者帮助金额分别为150、300。则最多可以认领4名学生。(金额300的志愿者认领200、50、45这3名学生,金额150的志愿者认领145这1名学生)
输入描述:
第一行输入一个正整数M(1
第三行输入一个正整数N(1
输出描述:
输出一个整数,表示N名志愿者最多可以认领多少名贫困学生
样例输入:
5
200 145 240 50 45
2
150 300
样例输出:
4
#include
#include
#include
using namespace std;
int m,n,a[205],b[55],cnt;
void dfs(int p,int sum){
if(p>m) return;
for(int i=1;i<=n;i++){//被选走的情况
if(b[i]>=a[p]){
b[i]-=a[p];
cnt=max(cnt,sum+1);
dfs(p+1,sum+1);
b[i]+=a[p];
}
}
dfs(p+1,sum);//不选的情况
}
int main()
{
cin>>m;
for(int i=1;i<=m;i++) cin>>a[i];
cin>>n;
for(int i=1;i<=n;i++) cin>>b[i];
dfs(1,0);//从第1本书开始搜索,已赞助0人
cout< 编程题5:路线(80分)
题目描述:
有一个旅游景区,景区中有N个景点,景点以数字1到N编号,其中编号为N的景点为游客服务中心所在地。景区中有M条连接路线,每条路线连接两个景点。
已知:
1)一个景点可以被多条路线连接;
2)景点之间的连接路线都可以双向行走;
当给出N个景点和M条连接路线,及M条路线的连接关系,请你计算出从编号1到编号N-1的每一个景点,到达游客服务中心至少需要经过几条路线,如果某个景点不能到达游客服务中心则输出“-1”。
例如:N=5,M=4,4条路线的连接关系为:1<->2、1<->3、2<->4、2<->5,
景点1到达景点5(游客服务中心)至少经过2条路线(路线2、路线4);
景点2到达景点5(游客服务中心)至少经过1条路线(路线4);
景点3到达景点5(游客服务中心)至少经过3条路线(路线1、路线2、路线4);
景点4到达景点5(游客服务中心)至少经过2条路线(路线3、路线4);

输入描述:
第一行输入两个正整数N和M(4<=N<=100,1<=M<=100),N表示景点个数,M表示路线条数,两个正整数之间一个空格隔开
接下来输入M行,每行包括两个正整数S,E(1≤S≤N,1≤E≤N,S!=E),两个正整数之间一个空格隔开,表示编号S和编号E的两个景点有一条路线连接
输出描述:
一行输出多个整数。按照1到N-1的编号顺序,分别输出每个景点到达编号N(游客服务中心),经过几条路线可以到达,如果某个景点不能到达则输出“-1”,整数之间一个空格隔开
样例输入:
5 4
1 2
1 3
2 4
2 5
样例输出:
2 1 3 2
#include
#include
#include
#include
using namespace std;
int n,m,s,e;
int a[110][110];//邻接矩阵
int p[110];//每个点的距离
int v[110];//是否经过
struct node{
int id,len;
};
queue q;
void bfs(int t){
q.push(node{t,0});
v[t]=1;p[t]=0;
while(!q.empty()){
node tt=q.front();
q.pop();
for(int i=1;i>n>>m;
for(int i=1;i<=m;i++){
cin>>s>>e;
a[s][e]=1;
a[e][s]=1;
}
bfs(n);
for(int i=1;i 编程题6:奖品(100分)
题目描述:
有一个N*M的矩阵方格,其中有些方格中有奖品,有些方格中没有奖品。小蓝需要从N*的矩阵中选择一个正方形区域,如果所选的正方形区域的一个对角线方格中都有奖品,其他方格都没有奖品,就会获得所选区域中的所有奖品,否则不能获得奖品。
当给出N和M的值,及N*M的矩阵方格中摆放的奖品情况(0表示方格中没有奖品,1表示方格中有奖品),请你帮助小蓝找出一个正方形区域,能够获得数量最多的奖品,并将奖品数输出。
例如:N=5,M=6,奖品情况如下:
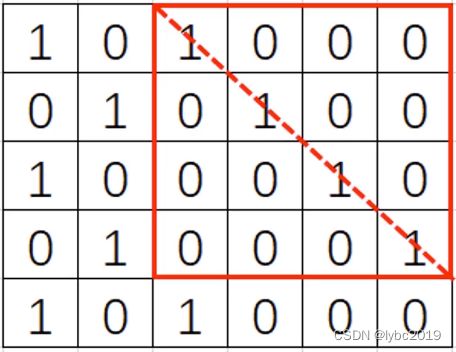
选择上图红色正方形区域,可以获得最多的4个奖品。
输入描述:
第一行输入两个整数N和M(1≤N≤100,1≤M≤100),N表示矩阵的行数,M表示矩阵的列数,两个整数之间一个空格隔开,接下来输入M行,每行包括M个0或者1(0表示方格中没有奖品,1表示方格中有奖品),0或者1之间一个空格隔开
输出描述:
输出一个整数,表示最多可以获得的奖品数
样例输入:
5 6
1 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
0 1 0 0 0 1
1 0 1 0 0 0
样例输出:
4
#include
#include
#include
#include
using namespace std;
int n,m,a[105][105],dp[105][105],maxn;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(a[i][j]==1 ){
int flag=0;
for (int x=i-1;x>=i-dp[i-1][j-1];x--)
if(a[x][j]==1){
flag=1;break;
}
for (int y=j-1;y>=j-dp[i-1][j-1];y--)
if(a[i][y]==1){
flag=1;break;
}
if(flag==0) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=1;
maxn=max(maxn,dp[i][j]);
}
}
cout<