论文解读-一个ANN (人工神经网络)chaotic generator的FPGA硬件设计与实现
论文标题:Hardware design and implementation of a novel ANN-based shaotic generator in FPGA
论文来源:sci-hub
简单概述一下这篇文章的摘要,本篇文章提出了一个新奇的人工神经网络的硬件实现,用于解决 Pehlivan–Uyaroglu Chaotic System (PUCS)问题建模在FPGA上的硬件实现。工作被分为两部分,首先在Matlab R2015a上实现了一个3-8-3的前向传播网络(FFNN),用反向传播算法进行训练后达到令人满意的准确率;第二部分则是训练后的网络的硬件实现。设计结构使用了VHDL语言,并且在Xilinx Virtex 6芯片上实现了设计。所提出的工作展示了混沌系统可以成功地在FPGA上用ANNs建模。
1.Introduction
这一部分主要就是介绍对真实世界进行建模分析是很重要的,并且很多问题都涉及到建模技巧。而混沌系统又是十分复杂的,对其建模仍是一个有挑战性的工作(主要是表现出工作的意义)。另外对混沌系统长期行为的预测,必须知道整体的初始条件。同时也介绍了人工神经网络对于解决此类问题是非常适合的。本次解读主要关注在硬件实现上,ANNs的平行处理结构使它实时应用中,需要大量平行计算能力,而硬件实现完美的匹配了这个特点。软件实现对比硬件实现确实执行速度相对较慢。(但软件实现方便)
硬件分为模拟系统与数字系统,模拟系统更精确但难以存储网络权重,所以才用噪声抗性高的数字系统。另外,选取FPGA芯片则是因为其强大的可重构性,模块化和动态适应性非常适合神经网络计算。
2.Chaotic systems
混沌主要表达的时候,我们很难通过单一的关系去预测一个非线性系统,需要整体的,连续的数据才能解释以及预测行为。这里引用维基百科上面的混沌系统的特质:
- 受初始状态影响的敏感性,初始条件非常微小的变动也可以导致最终状态的巨大差别。
- 具有拓扑混合性;不严格地来说,就是系统会将初始空间的拓扑性质彻底打乱,使得任何初始状态变换到其他任何位置。
- 周期轨道稠密,即在任何初始值附近都可以找到具有周期轨道的值。
文章中的PUCS就是一个混沌系统,而这里采用了RK5算法,迭代的计算分析,得到了系统基于初始条件随时间变化的图像:
3.Artificial Neural Network for modeling
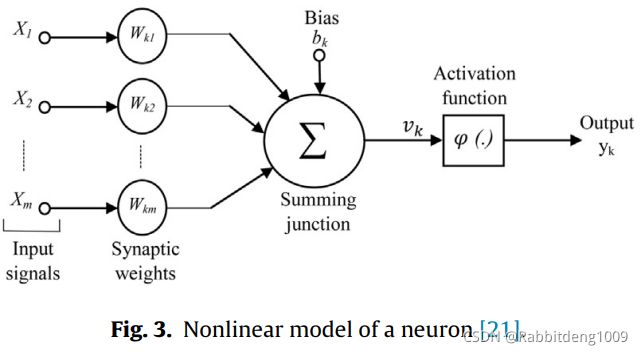
这一节主要就是介绍采用的ANN,在我们现在看来是一个很简单的神经网络架构,前向传播就是它的预测过程,后向传播则是用来训练的。论文中图片Fig.3描述了一个神经元的结构,它是非线性的:
第k个神经元的等式以下形式列出:
x代表输入信号,w则是权重,u是输入信号经过线性加法器的输出。b则是偏置量。ϕ(.)则是激活函数。y为输出信号。
这里使用了sigmoid function(又称为s函数),下面给出他的图像。实际上这个函数可以把属于(−∞, ∞)区间的输入映射到(0, 1)的开区间上。这就非常适合神经网络了,因为它的区间可以限制网络中信号的绝对值不会过大。
sigmoid函数的数学公式:
这里存在着指数函数,而数字系统中难以实现。本次解读重点关注对于sigmoid函数是怎么实现的。
下面提到的MSE,RMSE, NMSE则是用在后向传播过程中衡量error的量:
这里就不过多介绍后向传播过程了,这是深度学习基础知识,另外对于我们想要实现的前向传播过程,并不是必要了解的。
4. Field Programmable Gate Arrays
这里便是介绍FPGA的基本架构如何如何适合构造神经网络了,本次解读也建立在读者大概了解FPGA结构的基础上。FPGA就是一堆可编程逻辑单元,输入输出模块,连接模块构成的。
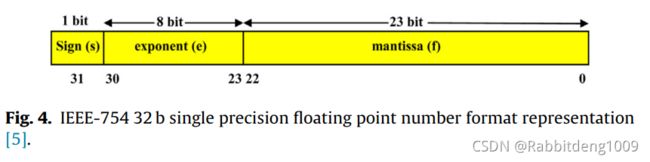
重点关注的是其中的数据表示,我们知道,硬件上这些数据都是由二进制表示的,这就引入了很多误差,如何减小误差呢?数据表示便非常重要了,一点点的误差也会对后向传播的过程造成巨大影响(很容易理解嘛,因为后向传播就是利用导数去一次次的修正网络参数。但这里其实需要注意,最影响的就是后向传播过程,实际网络进行工作的时候我们关注的是前向传播的准确性,而我们如果是在软件上训练之后把数据输入FPGA,只在FPGA上实现前向传播,这些误差其实对于网络精确率影响是有限的)有很多种浮点数的硬件表示方式被提出,这里采用了IEEE-754来表示单精度浮点数。见Fig.4:
Sign这一bit表述符号位,8bit的exponent则是指数位,23位mantissa则是浮点数位。通过Eq.10则可以将此浮点数形式转换为十进制数字:
5.Implementation ANN-based PUCS
通过Fig.5,以及论文中的描述,它先用Matlab Neural Network Processing Toolbox建立FFNN并在Matlab里面对它训练(offline training stage,应该是指的是并不是在FPGA板上训练的意思)然后对参数(w,b)进行保存后,输入到Xilinx FPGA的寄存器中,便可以在硬件上构造出相应的FFNN,输入矩阵传入FPGA,再得到相应的输出矩阵。
其实不用把这个FPGA实现过程想的太复杂,我们平常CPU执行,是指令一条条地进入指令寄存器,再处理数据寄存器等等。而FPGA是通过硬件电路写出了指令,不需要一条条读取指令,因为指令就是电路结构。这里说的简单一点,就是把网络结构写成了电路放在FPGA芯片上。
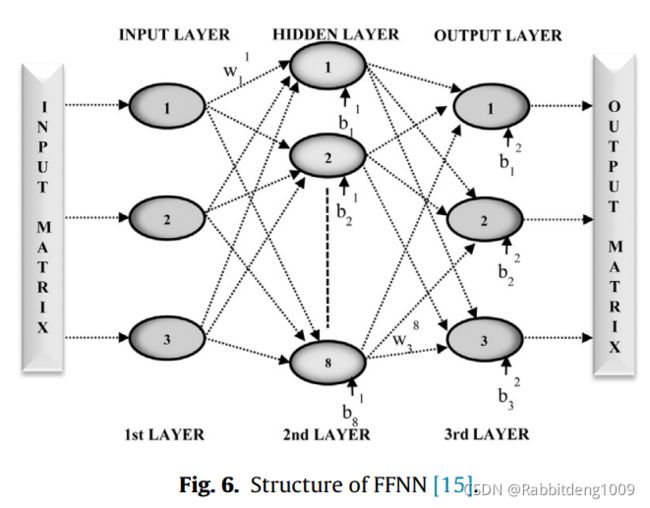
Fig.6就是这里使用的3-8-3网络结构,一共才14个神经元,与我们现在动辄百万级的深度神经网络确实差别很大,不过这就是这篇文章适合入手了解神经网络硬件实现的原因嘛。
输入矩阵是对RK5算法所产生结果的10,000个采样。输入,输出代表了PUCS的状态变量与输入的迭代过程。训练后的权重数据通过VHDL以单精度浮点数形式写入FPGA。全部的coding过程在Xilinx ISE 软件工具中综合与布线。仿真则是在ISE Project Navigator中。
重点来了,对激活函数的近似。前面说到了sigomid function是不能直接在FPGA上实现的,就要想办法替代它的效果,文章也提到了有以下方法:Piece-Wise Linear Approximation, Lookup Tables, Taylor Series Approximation and Elliot sigmoid Approximation。文章采用了另外的方式,这种方式组合了COordinate Rotation DIgital Computer (CORDIC)与Lookup Table (LUT)来近似计算。Eq.11说明了指数函数完全可以用三角函数进行替代:
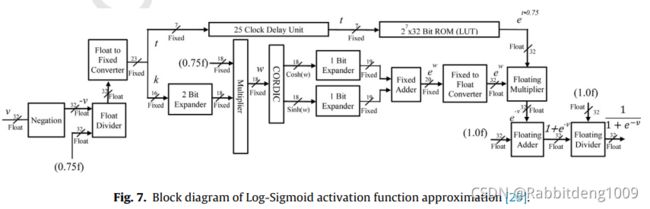
作者将CORDIC的sin h(v) and cos h(v)输出用 fixed-point adder(定点加法器)求和。通过基于CORDIC的指数计算器,作者设计了Log-Sigmoid activation function。Fig.7展示了其逻辑设计:
(以上设计还没有进行系统的学习,因为需要对比其他方法,这种方法的实际可行性与性能是否足够优秀还值得考究,所以就不进行介绍了,感兴趣的同学可以看原文)
6.Results
Fig.8就是最后完整设计的时序图输出。
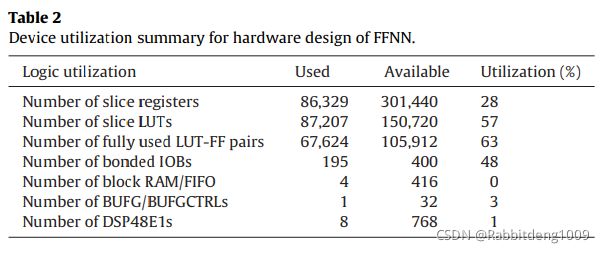
Table.2展示了本文设计所使用的资源数量与利用率,可以看到利用率并不高,因为本身的网络结构就十分简单。(本人没有使用过Xilinx Virtex 6这个板子,所以不清楚其性能,也无法点评作者的实现是否是足够资源友好的)
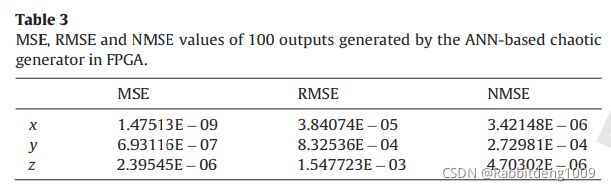
Table.3则是展示了从各种输出误差衡量方式来看,作者的最后预测输出都算是足够优秀了,(以RK5算法的预测结果作为了Ground Truth)。当然他这里算是一个回归问题,我们今后的应用,比如手写数字识别,是个分类问题,我们就需要不同的误差衡量方法了。
对于文章的主要贡献,作者说:“本文的主要贡献是,第一次的论文形式地,发表了关于在FPGA上用ANN对混沌系统进行建模”。对于我们读者来说,目前读这篇文章,不失为入手FPGA实现深度学习的一个好手段,可以系统的了解在FPGA上实现一个简单的神经网络架构需要什么经过哪些步骤,以及为什么我们要在硬件上实现神经网络来建模。当我们了解到,神经网络硬件实现的可行性后,便不由自主地思考,当更复杂的网络可以在FPGA上实现后,它可以带来多少神奇的应用了,智能汽车,无人机,机器人等,搭载了这样一块具有极低延迟的“大脑”,将会对他们的工作方式以及人类的未来造成巨大的改变。这也是我们为什么要学习硬件加速深度学习的初衷。
欢迎同学们一起讨论学习并指出我的错误。
文章图片来源于论文中或者维基百科,如有侵权立即联系本人进行删除。感谢!