hustlei

人工智能导论(6)——机器学习(Machine Learning)

文章目录

一、概述
二、重点内容
三、思维导图
四、重点知识笔记
- 1. 概述
- - 1.1 基本概念
  - 1.2 机器学习的分类
- 2. 常见有监督学习算法
- - 2.1 线性回归
  - 2.2 多项式回归
  - 2.3 支持向量机
  - 2.4 k-最近邻分类
  - 2.5 朴素贝叶斯
  - 2.6 决策树
  - 2.7 集成学习算法—Bagging算法、随机森林算法与Boosting算法
- 3. 常见无监督学习算法
- - 3.1 k-均值聚类算法
- 4. 深度学习
- 5. 强化学习

一、概述

学习能力是智能的重要标志之一。机器学习是人工智能的核心研究课题之一。

为方便记忆和回顾，根据个人学习，总结人工智能基础知识和思维导图形成系列。

二、重点内容

机器学习的基本概念
机器学习的过程和分类
常见有监督学习算法(回归、分类)
常见无监督学习算法(聚类)
强化学习
深度学习、进化计算(比较特别的有监督学习)

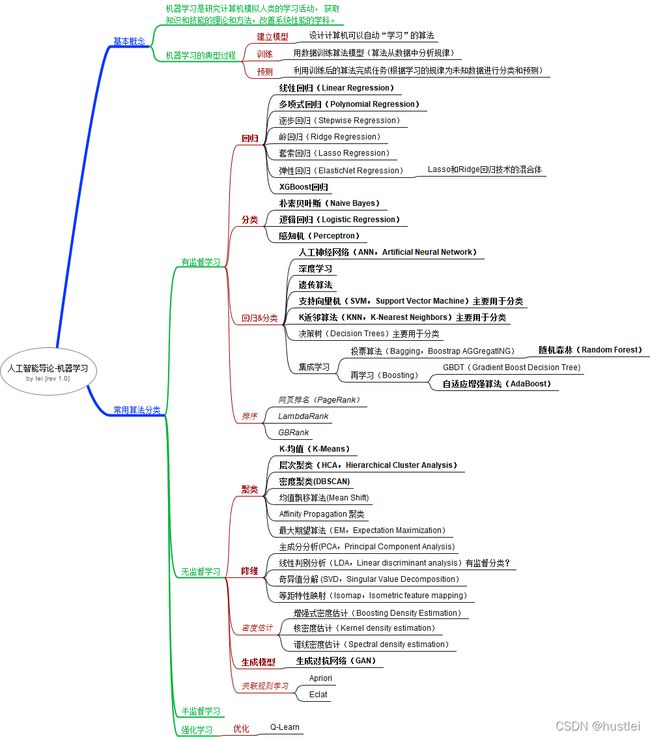
三、思维导图

四、重点知识笔记

1. 概述

1.1 基本概念

学习的概念

学习是一个有特定目的的知识获取和能力增长过程。
学习的内在行为是获得知识、积累经验、发现规律等
学习的外部表现是改进性能、适应环境、实现自我完善等。

机器学习的概念

直观上理解，机器学习（Machine Learning，ML）是研究计算机模拟人类的学习活动，获取知识和技能的理论和方法，改善系统性能的学科。

机器学习的过程

因为计算机系统中“经验‘通常以数据的形式存在，所以机器要利用经验，就必须对数据
进行分析。因此其过程可以简述如下：

建立模型：设计计算机可以自动“学习”的算法
训练：用数据训练算法模型（算法从数据中分析规律）
预测：利用训练后的算法完成任务(根据学习的规律为未知数据进行分类和预测）

1.2 机器学习的分类

（1） 按学习任务分类

回归、分类、聚类是机器学习最常见的三大任务。

回归是一种数学模型，利用数据统计原理，对大量统计数据进行数学处理，确定因变量与某些自变量的相关关系，建立一个相关性较好的回归方程（函数表达式）。

分类就是对数据分进行分类，把它们分到已知的每一个类别。

聚类就是对未知类别的样本进行划分，将它们按照一定的规则划分成若干个类族，把相似(距高相近)的样本聚在同一个类簇中。

降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中，用一个相对低维的向量来表示原始高维度的特征。

密度估计是是概率统计学的基本问题之一，就是由给定样本集合求解随机变量的分布密度函数问题。大多数人已经熟悉了其中一种常用的密度估计技术：直方图。

排序学习是信息检索和搜索引擎研究的核心问题之一，通过机器学习方法学习一个分值函数对待排序的候选进行打分，再根据分值的高低确定序关系。

主要算法有：

回归(Regression）-有监督学习（连续的）
- 线性(最小二乘)回归（Linear Regression）
- 多项式回归（Polynomial Regression）
- 逐步回归（Stepwise Regression）
- 岭回归（Ridge Regression）
- 套索回归（Lasso Regression）
- 弹性网回归（ElasticNet Regression）Lasso和Ridge回归技术的混合体
- XGBoost回归
- 泊松回归（Poisson Regression）
分类(Classification）-有监督学习（离散的）
- 朴素贝叶斯（Naive Bayes）
- 逻辑回归（Logistic Regression）
- 感知机（Perceptron）
- 距离判别法
回归+分类（可用于分类，也可以用于回归的算法）-有监督学习
- 人工神经网络（ANN，Artificial Neural Network）
- 深度学习
- 遗传算法
- 支持向量机（SVM，Support Vector Machine）主要用于分类
- K近邻算法（KNN，K-Nearest Neighbors）主要用于分类
- 决策树（Decision Trees）主要用于分类
- 集成学习（Ensembale Learning）其他算法进行组合的一种形式，主要用于分类
  - 投票算法（Bagging，Boostrap AGGregatING）
    - 随机森林（Random Forest）多个决策树投票决定结果
  - 再学习（Boosting）从一些弱分类器中创建一个强分类器的集成技术
    - GBDT（Gradient Boost Decision Tree)决策树的boosting算法
    - 自适应增强算法（AdaBoost）
聚类（Clustering）-无监督学习
- K-均值（K-Means）基于原型的目标函数聚类方法
- 层次聚类（HCA，Hierarchical Cluster Analysis）
- 密度聚类(DBSCAN)
- Affinity Propagation 聚类
- 均值飘移算法(Mean Shift)
- 单链聚类（Single-linkage clustering）
- 概念聚类（Conceptual clustering）
- 模糊聚类（Fuzzy clustering）
- 密度峰值聚类（Clustering by desity peaks）
- 最大期望算法（EM，Expectation Maximization）
降维（Dimensionality reduction）-无监督学习
- 主成分分析(PCA，Principal Component Analysis)
- 奇异值分解(SVD)
- 线性判别分析（LDA，Linear discriminant analysis）
- 等距特性映射（Isomap，Isometric feature mapping）
- 核主成分分析（Kernel PCA）
- 基于图的核PCA（Graph-based kernel PCA）
- 广义判别分析（GDA，Generalized discriminant analysis）
- 多维尺度分析（MDS，Multi-dimensional Scaling）
密度估计（Density estimation）-无监督学习
- 增强式密度估计（Boosting Density Estimation）
- 核密度估计（Kernel density estimation）
- 谱线密度估计（Spectral density estimation）
- 平均积分平方误差（MISE，Mean integrated squared error）
- 分布式核嵌入（Kernel embedding of distributions）
排序（Ranking）-有监督学习
- 网页排序（PageRank）
- AdaRank
- BayesRank
- RankBoost
- RankSVM
- RankNet
- LambdaRank
- GBRank
优化（Optimization）
- Q-学习（Q-learning）

（2）按学习方式分类

有监督学习指利用一组带标签的数据（已知输出的数据）训练学习模型，然后用经训练的模型对未知数据进行预测。

无监督学习根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题。

强化学习（Reinforcement Learning，RL）又称为再励学习、评价学习，是一种通过模拟大脑神经细胞中的奖励信号来改善行为的机器学习方法。

有监督学习（Supervised）
- 回归
- 分类
- 排序
无监督学习
- 聚类
- 降维
- 密度估计
- 生成模型
  - 生成对抗网络（GAN）
- 关联规则学习（Association rule learning）
  - Apriori
  - Eclat
半监督学习（Semi-supervised）
强化学习（Reinforcement）
- 无模型的
  - 策略优化（Policy Optimization）
  - 优化 Q-Learning
- 有模型的
  - AlphaZero

（3）按学习模型划分

模型	简单说明	子模型	典型算法
Geometric 几何	采用线、面、距离或流形等几何模型构建学习算法	Line 线	Linear Regression 线性回归
		Plane 面	SVM 支持向量机
		Distance 距离	k-NN k近邻
		Manifold 流形	Isomap 等距映射
Logical逻辑	采用逻辑模型构建学习算法	Logic逻辑	Inductive Logic Program归纳逻辑编程
Logical逻辑	采用逻辑模型构建学习算法	Rule规则	Association Rule相关规则
Network 网格	采用网络模式构建机器学习算法	Shallow 浅层	Perceptron 感知机
Network 网格	采用网络模式构建机器学习算法	Deep 深层	CNN 卷积神经网络
Probabilistic 概率	采用概率模式来表示随机变量之间的条件相关性	Bayes 贝叶斯	Bayesian Network 贝叶斯网络
		Generative 生成	Probabilistic Program 概率规划
		Statistic 统计	Linear Regression 线性回归

其他分类方法

基于学习方法的分类
- 归纳
- 演绎
- 类比
- 神经学习
基于学习策略的分类
- 符号主义：从逻辑学与哲学出发，认知即为计算，通过对符号的演绎推理来达到结果
- 贝叶斯派：从统计学出发，利用统计方法解决不确定性问题
- 联结主义：从神经科学出发，对大脑进行模拟仿真
- 行为类比主义：从心理学出发，研究新旧知识之间的相似性
- 进化主义：从进化生物学出发，使用遗传算法模拟进化过程

2. 常见有监督学习算法

回归、分类、排序算法都属于有监督的学习。在实际应用中，机器学习主要以有监督的学习为主。

有监督的学习的一个典型特征为：拿已知结果的数据对模型进行训练。

单层感知机、CNN和RNN网络模型也都属于有监督的模型。

2.1 线性回归

线性回归是最简单的回归算法。

线性回归假定输入变量（X）和单个输出变量（Y）之间呈线性关系。即

y = wx+b

其中，x=(x1,x2,…,xn) 为n维输入变量，w=(w1,w2,…,wn)为线性系数，b是偏置项。
目标是找到系数w的最佳估计，使得预测值Y的误差最小。

通常使用最小二乘法估计w和b，即：使样本的y值与y=wx+b预测的值之间的差的平方和最小。

2.2 多项式回归

像线性回归一样，多项式回归使用多项式变量x和y之间的关系，可以是二阶多项式、三阶多项式，也可以是n阶多项式。

比如：

y = ax**2+bx+c
y = ax1**2+bx2**2+cx1x2+dx1+ex2+f

2.3 支持向量机

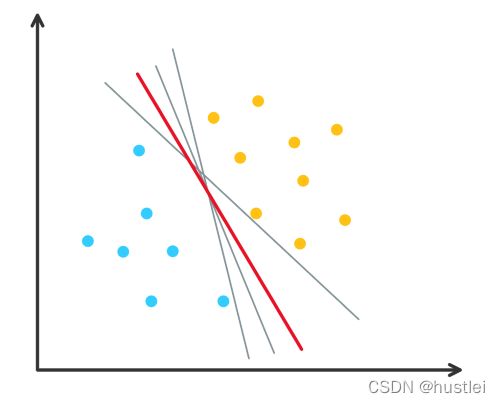
支持向量机是最受欢迎、讨论最广的机器学习分类方法之一。是一种线型分类器。

基本原理：

在二维空间内，超平面可被视为一条直线，假设所有的输入点都可以被该直线完全分开，
两类边界由超平面式g(x)决定。

g(x) = wx-b=0
w为法向量，b为阈值，根据带标签的数据训练求出

SVM的目标：找到一组分割系数w、b，使一个超平面能够对数据x进行最佳分割，即能将两类正确分开，且分类间隔最大。

主要优点：

可以解决高维问题，即大型特征空间
可以解决小样本下机器学习问题
能够处理特征的相互作用
泛化能力比较强

主要缺点：

当观测样本很多时，效率并不高
对非线性问题没有通用的解决方案

2.4 k-最近邻分类

k-最近邻（K-NN，k-NearestNeighbor）可用于分类，也可用于回归。
K-NN分类是最简单的多分类技术。

K-NN基本原理：

K-NN分类的基本概念是找到与新样本距离最近的K个训练样本(已确定分类)。
新样本从K个已确定分类的邻居获得分类标签。

对于回归问题，它可能是输出变量的平均值；

对于分类问题，它可能是模式类别值。

主要过程：

1. 计算训练样本和测试样本中每个样本点的距离
+ 常见的距离度量
- 欧氏距离（最常见）
- 曼哈顿距离
- 明氏距离
- 切氏距离
2. 对计算所得所有距离值进行排序
3. 对每个测试样本点选前k个最小距离的训练样本
4. 根据这k个训练样本的标签进行投票，得出测试样本点的预测分类

2.5 朴素贝叶斯

朴素贝叶斯也称为简单贝叶斯，是一种十分简单的分类算法。
朴素贝叶斯分类器的基础是贝叶斯定理。

P(类别|特征) = P(特征,类别)/P(特征) = P(特征|类别)P(类别)/P(特征)

以特征=咳嗽，类别=肺炎为例：

P(咳嗽)：咳嗽的概率

P(肺炎）：肺炎的概率

P(咳嗽,肺炎)：咳嗽且得肺炎的概率

P(肺炎|咳嗽)：在已知咳嗽的条件下，肺炎的概率

P(咳嗽|肺炎)：在已知得肺炎的条件下，咳嗽的概率

P(肺炎)为先验概率，即已知的根据经验或统计直接估计的概率

P((咳嗽|肺炎)为已知结果，出现某个特征的条件概率

所以已知先验概率和条件概率，就可以对已知特征进行分类。

实际情况中，特征会有多个，比如肺炎可能具有咳嗽、疼痛、流鼻涕、鼻塞等多个特征。假设特征相互独立，就可以用全概率公式计算多个特征时的概率。因此，朴素贝叶斯模型假设特征之间相互独立。

朴素贝叶斯分类算法的特点：

朴素贝叶斯模型与其他分类方法相比具有较小的误差率。
朴素贝叶斯模型实际应用效果并不理想，因为实际应用中特征之间往往并不是相互独立的

2.6 决策树

决策树（Decision Tree）是一种基本的分类与回归方法，此处主要指分类的决策树。

决策树算法的基本原理：

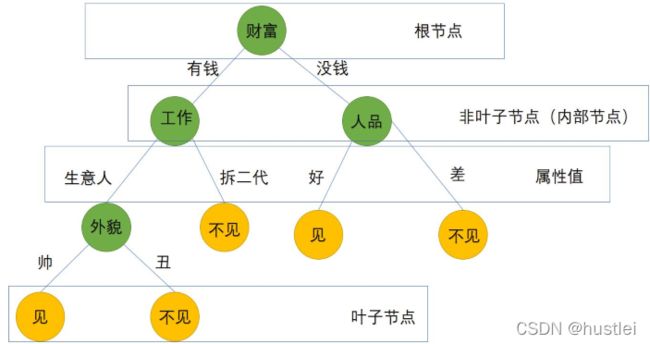
决策树是一种树形结构
每个节点表示一个特征分类测试，且仅能存放一个类别
每个分支代表输出
从决策树的根结点开始，选择树的其中一个分支，并沿着选择的分支一路向下直到树叶
将叶子节点存放的类别作为决策结果

2.7 集成学习算法—Bagging算法、随机森林算法与Boosting算法

集成学习是将多个分类器集成在一起的技术。可以用与回归，也可以用于分类。

集成学习用于分类的基本思路：

通过从训练数据中选择不同的子集来训练不同的分类器
然后使用某种投票方式综合各分类器的输出，最终输出基于所有分类器的加权和。

最流行的集成分类技术包括：Bagging算法、随机森林算法、Boosting算法

Bagging算法

套袋（Bagging）算法是一种最简单的集成学习方法。

流程：

对给定数据集进行有放回抽样，产生m个新的训练集
训练m个分类器，每个分类器对应一个训练集
通过m个分类器对新的输入进行分类预测
选择各个分类器“投票”最多的类别，即大多数分类器选择的类别。

Bagging算法的分类器可以选用SVM、决策树、DNN等。

随机森林算法

随机森林是当今最流行的套袋集成技术，由许多决策树分类器组成，并利用
Bagging算法进行训练。

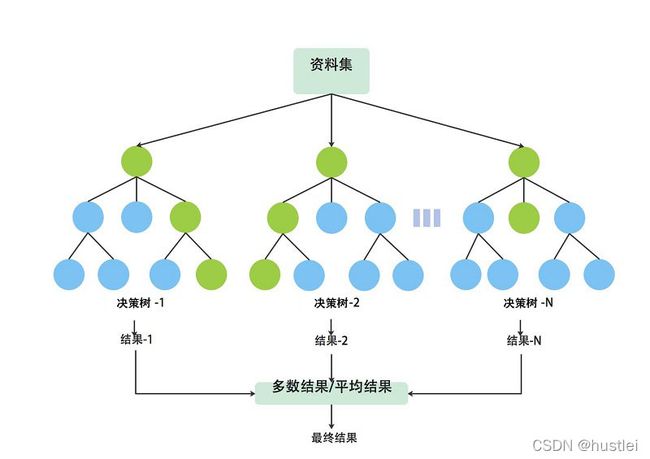
随机森林算法基本思路：

首先，输入变量穿过森林中的每棵树
然后，每棵树会预测出一个输出类别，即树为输出类别“投票”
最后，森林选择获得树投票最多的类别作为它的输出

过程：

与Bagging算法一样，对原始训练数据集进行n次有放回的采样，并构建n个决策树。
使用样本数据集训练决策树
- 从根节点开始，在后续的各个节点处，随机选择一个由m个输入变量构成的子集
- 在对这m个输入变量进行测试的过程中，将样本分为两个单独类别
- 对每棵树都进行这样的分类，直到该节点的所有训练样本都属于同一类。
将生成的多棵分类树组成随机森林，用随机森林分类器对新的数据进行分类
通过多棵树分类器投票决定最终的分类结果。

随机森林的特点：

在具有大量输入变量的大数据集上表现良好、运行高效
它训练快速并且可调，同时不必像SVM那样调整很多参数

所以在深度学习出现之前一直比较流行。并且经常会成为很多分类问题的首选方法。

Boosting算法

Boosting算法是一种框架算法。

它首先会在对训练集进行转化后重新训练出分类器，即通过对样本集进行操作获得样本子集，然后用弱分类算法在样本子集上训练生成一系列的分类器，从而对当前分类器不能很好分类的数据点实现更好的分类。

Boosting主要算法有:

自适应提升（Adaptive Boosting，AdaBoost）
梯度提升决策树（GradientBoosting Descision Tree，GBDT）

AdaBoost是一种迭代算法。

初始时，所有训练样本的权值都被设为相等，在此样本分布下训练出一个弱分类器。
在第n（n=1,2,3,…,T）次迭代中，样本的权值由第n-1次迭代的结果决定。
在每次迭代的最后，都有一个调整权值的过程
- 被分类错误的样本将得到更高的权值，从而使分类错误的样本被突出，得到一个新的样本分布。
在新的样本分布下，再次对弱分类器进行训练，得到新的弱分类器。
经过T次循环，会得到T个弱分类器，把这T个弱分类器按照一定的权值叠加起来，就可以得到最终的强分类器。

Boosting算法与Bagging算法的不同之处：

Boosting算法的每个新分类器都是根据之前分类器的表现而进行选择的
Bagging算法中，在任何阶段对训练集进行重采样都不依赖之前分类器的表现
Boosting算法的目标是基于弱分类器的输出构建一个强分类器，以提高准确度

Boosting算法的主要应用领域包括模式识别、计算机视觉等，
其可以用于二分类场景，也可以用于多分类场景。

3. 常见无监督学习算法

聚类、降维算法都是无监督学习算法

聚类算法根据数据的特征，将数据分割为多个集合，每个集合称为一个聚类。

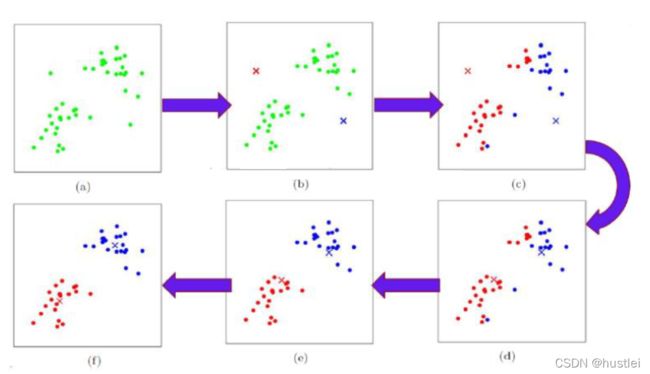
3.1 k-均值聚类算法

k-均值聚类算法将对象根据它们的特征分割为k个聚类。

k-means聚类算法中k表示为样本分配的聚类的数量。

k-means聚类算法是一种迭代求解的算法，基本思路：

可以使用一个随机特征向量来对一个聚类进行初始化
将其他样本添加到其最近邻的聚类中
- （假定每个样本都能表示一个特征向量，并且可以使用常规的欧氏距离式来计算距离）。
随着一个聚类所添加的样本越来越多，其形心（即聚类的中心）会重新计算，然后该算法就会重新检查一次样本，以确保它们都在最近邻的聚类中，直到没有样本需要改变所属聚类为止。k-均值聚类算法由于操作简单、容易实现

随机选取K个对象作为初始的聚类中心
计算对象与聚类中心之间的距离，把对象分配给距离它最近的聚类中心
每分配一个样本，根据对象重新计算聚类中型
不断重复2-3，直到满足终止条件。
- 终止条件可以是：
  - 没有（或最小数目）对象被重新分配给不同的聚类
  - 没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。.

4. 深度学习

传统机器学习一般善于处理小规模数据问题。对于大规模数据，尤其对于图像类型的数据，人工很难获得数据特征以用于对图像进行分类，因此长期以来，传统机器学习产生的机器智能是十分有限的。直到深度学习出现之后才得以改观。

深度学习作为机器学习算法中的一个新兴技术，通常与深度神经网络有关联，是一种特殊的机器学习算法。

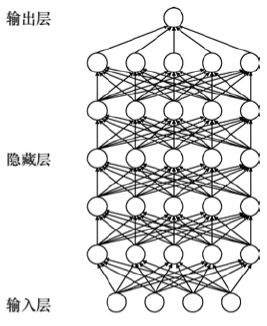
深度学习是使用多层人工神经网络进行学习的模型。
深度强调多层，但是没有特指几层（可以是5层、10层、几百、几千层）
深度学习通过逐层特征变换，将样本原空间的特征变换到新特征空间，使分类或预测更容易

与感知机相比：多层感知器实际是只含有一层隐藏层节点的学习模型。

本质是对数据进行分层特征表示，实现将低级特征通过神经网络来进一步抽象
成高级特征。

以辛顿为首的新联结主义者强调，神经网络深度优于宽度。

5. 强化学习