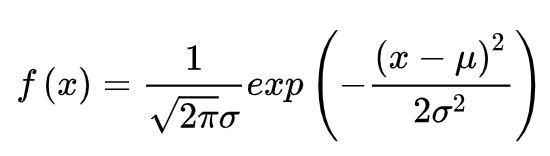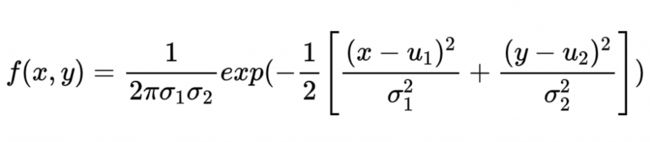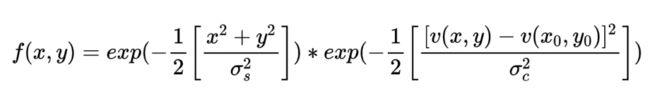OpenCV-Python教程:高斯平滑、双边平滑(GaussianBlur,bilateralFilter)
原文链接:http://www.juzicode.com/opencv-python-gaussianblur-bilateralfilter
返回Opencv-Python教程
OpenCV-Python教程:均值平滑、中值平滑 一文中介绍了在滑动窗口内均值的方式进行平滑处理,这时窗口中心点和窗口领域内的所有像素的加权系数都是一样的,中值平滑提取中位数时滑动窗口内任一像素出现中值的概率也是相同的。本文要介绍的高斯平滑则根据距离中心点的间距远近其权重会不同,这种方式看起来更符合”惯例”:身边的人对你影响会更大。
1、高斯平滑GaussianBlur()
所谓高斯平滑,闻其名就知道和”高斯”这位大神有关,这里实际用到的是高斯分布。我们先来看下一维高斯分布(正态分布)的概率密度函数:
这是一个以自然常数e为底的二次指数函数,其中μ是均值,σ是标准差,我们可以用matplotlib绘图,设置μ=0,σ=0.8:
#juzicode.com/vx:桔子code
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font',family='Youyuan',size='9')
plt.rc('axes',unicode_minus='False')
mu=0 #均值
sigma=0.8 #标准差
x=np.linspace(-3,3,60)
y=np.exp((-(x-mu)**2)/(2*(sigma**2)))/(np.sqrt(2*np.pi)*sigma)
plt.plot(x,y,"b-",)
plt.grid(True)因为在OpenCV的高斯平滑中用到的正态分布都是取μ=0,这里就不对比u值差异,只看下取不同的σ的曲线,
#juzicode.com/vx:桔子code
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font',family='Youyuan',size='9')
plt.rc('axes',unicode_minus='False')
x=np.linspace(-3,3,100)
mu=0 # 均值μ
sigma=0.3 # 标准差σ
y=np.exp((-(x-mu)**2)/(2*(sigma**2)))/(np.sqrt(2*np.pi)*sigma)
sigma=0.5
y2=np.exp((-(x-mu)**2)/(2*(sigma**2)))/(np.sqrt(2*np.pi)*sigma)
sigma=1.1
y3=np.exp((-(x-mu)**2)/(2*(sigma**2)))/(np.sqrt(2*np.pi)*sigma)
plt.plot(x,y,"b-",)
plt.plot(x,y2,"g-",)
plt.plot(x,y3,"r-",)
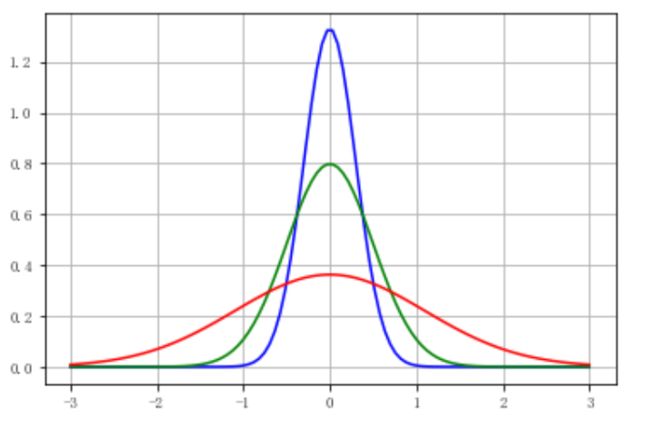
plt.grid(True)从高斯分布的曲线可以看到(μ=0时):
- 当x=0时,f(x)的值最大,当x向两边变化时,f(x)的值越来越小;
- 这个曲线在x=0的2侧是对称的,f(-1)=f(1),f(-2)=f(2);
- σ越大,曲线越平坦,x=0时的取值越低。
因为图像是二维的,实际上在OpenCV中要用到二维高斯分布,可以从一维高斯分布推导出二维高斯分布(这里假设x,y不相关),其中x表示邻域像素距离中心点水平方向的间距,y表示垂直方向的间距:
用matplotlib绘制二维高斯分布:
#juzicode.com/vx:桔子code
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(-3, 3.1, 0.1,dtype=np.float64).reshape(-1,1)
Y = np.arange(-3, 3.1, 0.1,dtype=np.float64)
mux,muy=0,0
sigmax,sigmay = 0.8,0.8
expont = -0.5*(((X-mux)/sigmax)**2 + ((Y-muy)/sigmay)**2)
Z=np.exp(expont)/(2*np.pi*sigmax*sigmay)
ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=cm.viridis)
plt.show()二维高斯分布也具备一维高斯分布类似的特点:在f(0,0)处取值最大(μ=0时),σ越大曲线越平坦。
有了前面绘制曲线得到的直观感受,下面我们用numpy构造一个5×5大小的高斯核(滑动窗口):
#juzicode.com/vx:桔子code
import numpy as np
X = np.arange(-2, 3, 1,dtype=np.float64).reshape(-1,1)#转置
Y = np.arange(-2, 3, 1,dtype=np.float64) #[-2. -1. 0. 1. 2.]
mux,muy=0,0
sigmax,sigmay = 0.8,0.8
expont = -0.5*(((X-mux)/sigmax)**2 + ((Y-muy)/sigmay)**2)
Z=np.exp(expont)/(2*np.pi*sigmax*sigmay)
Z=Z/np.sum(Z) #归一化
print(Z)[[0.00048091 0.00501119 0.01094545 0.00501119 0.00048091]
[0.00501119 0.0522178 0.11405416 0.0522178 0.00501119]
[0.01094545 0.11405416 0.2491172 0.11405416 0.01094545]
[0.00501119 0.0522178 0.11405416 0.0522178 0.00501119]
[0.00048091 0.00501119 0.01094545 0.00501119 0.00048091]]从这个5×5大小的矩阵也能看到,位于正中心的点取值为0.2491172是最大值的点,紧邻着正中心距离为1的周围4个点的值0.11405416是第2大的点,依次越往外取值越小。
GaussianBlur()的接口形式:
dst=cv2.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])- 参数含义:
- src:通道数任意,实际处理是分通道处理;图像深度只能是CV_8U, CV_16U, CV_16S, CV_32F or CV_64F;
- ksize:元组类型,窗口大小,宽度和高度可以不一样,但是必须是正的奇数;如果设置为0,则根据sigma计算得到。
- sigmaX:图像X方向的标准差,对应前述二维高斯分布的σ1;
- sigmaY:图像Y方向的标准差,对应前述二维高斯分布的σ2,如果传入0,会等于sigmaX,如果sigmaX和sigmaY都传入0,sigmaX和sigmaX则根据ksize计算;
- borderType:边界处理方式;
注意:GaussianBlur的首字母是大写的G,和其他大多数OpenCV函数名称采用小驼峰命名风格稍有差异。
因为都是以滑动窗口中心点为原点,为了保证中心点(x,y)=(0,0)的权重为最大值,所以在OpenCV的高斯平滑中μ1和μ2都设置为0,这样在调用高斯平滑函数时只需要传入σ1(sigmaX)和σ2(sigmaY)。
下面是用不同的ksize进行高斯平滑的例子:
import matplotlib.pyplot as plt
import cv2
print('VX公众号: 桔子code / juzicode.com')
print('cv2.__version__:',cv2.__version__)
plt.rc('font',family='Youyuan',size='9')
img = cv2.imread('..\\lena.jpg')
img_ret1 = cv2.GaussianBlur(img,(3,3),0)
img_ret2 = cv2.GaussianBlur(img,(5,5),0)
img_ret3 = cv2.GaussianBlur(img,(11,11),0)
#显示图像
fig,ax = plt.subplots(2,2)
ax[0,0].set_title('VX:桔子code 原图')
ax[0,0].imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB)) #matplotlib显示图像为rgb格式
ax[0,1].set_title('GaussianBlur ksize=3')
ax[0,1].imshow(cv2.cvtColor(img_ret1,cv2.COLOR_BGR2RGB))
ax[1,0].set_title('GaussianBlur ksize=5')
ax[1,0].imshow(cv2.cvtColor(img_ret2,cv2.COLOR_BGR2RGB))
ax[1,1].set_title('GaussianBlur ksize=11')
ax[1,1].imshow(cv2.cvtColor(img_ret3,cv2.COLOR_BGR2RGB))
ax[0,0].axis('off');ax[0,1].axis('off');ax[1,0].axis('off');ax[1,1].axis('off')#关闭坐标轴显示
plt.show() 从运行结果看,ksize越大,图像越模糊。
下面是ksize保持不变,sigmaX变化的例子(sigmaY不传入默认等于sigmaX):
import matplotlib.pyplot as plt
import cv2
print('VX公众号: 桔子code / juzicode.com')
print('cv2.__version__:',cv2.__version__)
plt.rc('font',family='Youyuan',size='9')
img = cv2.imread('..\\lena.jpg')
img_ret1 = cv2.GaussianBlur(img,(5,5),0.5)
img_ret2 = cv2.GaussianBlur(img,(5,5),10)
img_ret3 = cv2.GaussianBlur(img,(5,5),25)
#显示图像
fig,ax = plt.subplots(2,2)
ax[0,0].set_title('VX:桔子code 原图')
ax[0,0].imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB)) #matplotlib显示图像为rgb格式
ax[0,1].set_title('GaussianBlur ksize=5 sigma=0.5')
ax[0,1].imshow(cv2.cvtColor(img_ret1,cv2.COLOR_BGR2RGB))
ax[1,0].set_title('GaussianBlur ksize=5 sigma=10')
ax[1,0].imshow(cv2.cvtColor(img_ret2,cv2.COLOR_BGR2RGB))
ax[1,1].set_title('GaussianBlur ksize=5 sigma=25')
ax[1,1].imshow(cv2.cvtColor(img_ret3,cv2.COLOR_BGR2RGB))
ax[0,0].axis('off');ax[0,1].axis('off');ax[1,0].axis('off');ax[1,1].axis('off')#关闭坐标轴显示
plt.show() 对应到高斯分布曲线的特性,当sigma越大时,原点的取值越小,周围点的取值更大,对应到图像上中心点的权重越低,周围点权重越高,所以sigma越大图像越模糊。
2、双边平滑bilateralFilter()
均值、中值、高斯平滑的去躁是一种“无差别攻击”,所有的像素都受到同一个加权系数的影响,所以在平滑过程中也会影响到图像的边沿(像素值突变的地方),接下来要介绍的双边滤波则可以在去除噪声的同时又能保持图像的边沿,也就是传说中的”去噪保边”。
双边平滑使用的加权系数如下:
第1个exp()函数是空间距离加权系数的简化,1)前面的1/2πσ1σ2系数没有了,因为该系数在σ1和σ2确定后最后归一化的时候是会被消除掉的;2)双边平滑x和y方向用的σ1=σ2,所以用一个σs代替;3)u值在高斯平滑中也一直设置为0,这里也直接去掉了。其中x和y分别表示邻域像素和中心点X和Y方向的距离。
第2个exp()函数也是高斯函数,v(x0,y0)表示中心点的像素值,v(x,y)表示距离中心点距离为(x,y)的像素值,所以这部分的值就和像素差值有关。如果像素差值为0,这部分系数的值就为1,所以就等价于高斯平滑的系数;如果2个像素差值非常大,这个部分exp()系数就向0靠拢,最后的f(x,y)就向0靠拢,这时该像素值对中心点的影响就非常小。所以如果2个像素值差异非常大时,这时新生成图像的像素值就不会被这个差异极大的像素受影响,从而保持该差异,达到“保边”的效果。
2个exp()函数就是双边平滑的“双边”的含义,它并不是指图像的X和Y(行、列)2个方向,而是指在像素差和空间距离的2个“边”。
bilateralFilter()的接口形式:
dst=cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])- 参数含义:
- src:8bit或浮点类型;1或3通道;
- d:窗口大小,如果为非正数,根据sigmaSpace计算;d>5时速度会比较慢,当噪声比较严重时可以选择d>=9,但是此时不适合对时间敏感的处理;
- sigmaColor:亮度差的sigma参数;
- sigmaSpace:空间距离的sigma参数,同时作用于图像的X和Y(行、列)2个方向;
- borderType:边界处理方式;
在表示滑动窗口大小的参数里,高斯平滑的ksize参数是一个宽高可以不等的元组,但是双边平滑用的参数d是一个整型类型,这也决定了其滑动窗口宽高是相等的。另外d的大小在源码中是这样设置的:
if( d <= 0 )
radius = cvRound(sigma_space*1.5);
else
radius = d/2;
radius = MAX(radius, 1);
d = radius*2 + 1;如果d小于0,用sigma_space*1.5后取整得到半径,如果d大于0则先除以2得到半径radius,然后用半径radius和1比较取其中更大的值,最后乘以2加1,这样的得到的d可以保证是不小于3的奇数。
sigmaColor和sigmaSpace参数比较小的时候(<10),平滑的效果不是很明显,当参数比较大或者多次平滑后的图像看起来会比较卡通化,详情可阅读:论如何把自己变成卡通人物(OpenCV制作卡通化头像)。
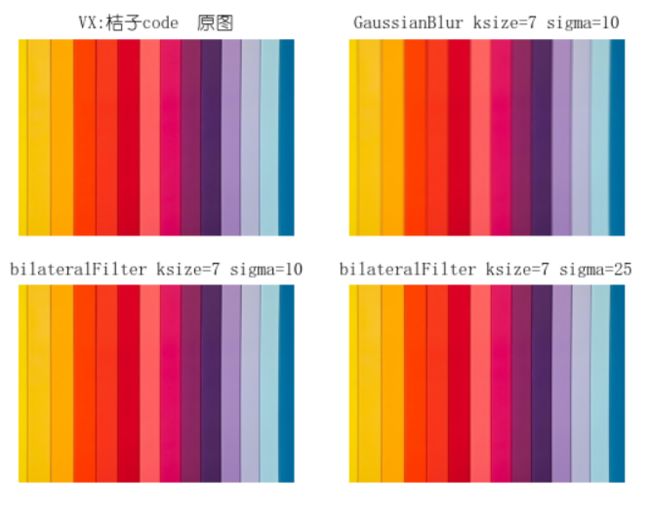
下面的是一个高斯平滑和双边平滑对比的例子,取相同的滑动窗口大小以及相同的sigma值,观察平滑后的差异,以及在平滑后取ksize=3计算sobel边沿:
import matplotlib.pyplot as plt
import cv2
print('VX公众号: 桔子code / juzicode.com')
print('cv2.__version__:',cv2.__version__)
plt.rc('font',family='Youyuan',size='9')
img = cv2.imread('..\\samples\\picture\\streak.jpeg')
img_ret1 = cv2.GaussianBlur(img,(7,7),10)
img_ret2 = cv2.bilateralFilter(img,7,10,10)
img_ret3 = cv2.bilateralFilter(img,7,25,25)
fig,ax = plt.subplots(2,2)
ax[0,0].set_title('VX:桔子code 原图')
ax[0,0].imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB)) #matplotlib显示图像为rgb格式
ax[0,1].set_title('GaussianBlur ksize=7 sigma=10')
ax[0,1].imshow(cv2.cvtColor(img_ret1,cv2.COLOR_BGR2RGB))
ax[1,0].set_title('bilateralFilter ksize=7 sigma=10')
ax[1,0].imshow(cv2.cvtColor(img_ret2,cv2.COLOR_BGR2RGB))
ax[1,1].set_title('bilateralFilter ksize=7 sigma=25')
ax[1,1].imshow(cv2.cvtColor(img_ret3,cv2.COLOR_BGR2RGB))
ax[0,0].axis('off');ax[0,1].axis('off');ax[1,0].axis('off');ax[1,1].axis('off')#关闭坐标轴显示
img_edge1=cv2.Sobel(img_ret1,cv2.CV_8U,1,0,ksize=3)
img_edge2=cv2.Sobel(img_ret2,cv2.CV_8U,1,0,ksize=3)
img_edge3=cv2.Sobel(img_ret3,cv2.CV_8U,1,0,ksize=3)
fig2,ax2 = plt.subplots(2,2)
ax2[0,0].set_title('VX:桔子code 原图')
ax2[0,0].imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB)) #matplotlib显示图像为rgb格式
ax2[0,1].set_title('GaussianBlur ksize=7 sigma=10')
ax2[0,1].imshow(cv2.cvtColor(img_edge1,cv2.COLOR_BGR2RGB))
ax2[1,0].set_title('bilateralFilter ksize=7 sigma=10')
ax2[1,0].imshow(cv2.cvtColor(img_edge2,cv2.COLOR_BGR2RGB))
ax2[1,1].set_title('bilateralFilter ksize=7 sigma=25')
ax2[1,1].imshow(cv2.cvtColor(img_edge3,cv2.COLOR_BGR2RGB))
ax2[0,0].axis('off');ax2[0,1].axis('off');ax2[1,0].axis('off');ax2[1,1].axis('off')#关闭坐标轴显示
plt.show()
平滑后的对比:
取sobel边沿对比:
从运行结果可看到,在颜色突然变化的地方(边沿),高斯平滑只保留了一半左右的边界,而双边平滑几乎将所有的边界保留下来,而且高斯平滑的边界亮度平均值也没有双边平滑高。
小结:高斯平滑对比均值和中值平滑其取值更符合“惯例”,在空间距离上距离越近的像素用来计算新像素的值其权重越大。均值平滑、中值平滑和高斯平滑会对整幅图像实现无差别的平滑,一个固定系数的滑动窗口作用于整个图像,所以平滑后的图像虽然处理掉了噪声,但是边沿部分也会被削弱。而双边平滑在高斯平滑使用的系数基础上乘以像素差值的高斯函数,和中心点像素差值越大整个系数值越小,最后就能达到去躁保边的效果。
扩展阅读:
- OpenCV-Python教程
- 论如何把自己变成卡通人物
-
有了这款神器,什么吃灰文件都统统现形
-
一行代码深度定制你的专属二维码(amzqr)
-
编码: 一个隐藏了30多年的bug,Windows含蓄说过某通不行?