日撸 Java 三百行（22 天: 二叉树的转储）

注意：这里是JAVA自学与了解的同步笔记与记录，如有问题欢迎指正说明

目录

一、二叉树转储及其原理

1.为什么要考虑二叉树的转储

2.层次遍历实现存储

二、链表二叉树转储为顺序表的代码

1.基本初始化与BFS

2.关于队列的准备

3.核心代码

4.完整代码

5.数据模拟

 总结

---

一、二叉树转储及其原理

1.为什么要考虑二叉树的转储

        我们上一章学习的二叉树的基本内容中提到了二叉树的遍历。实际上不同于线性结构，单独只知道二叉树的一个遍历是无法还原二叉树的，或者说，只能知道二叉树的中序遍历和任何一个前或后序遍历我们才能真正构造一个独一无二的二叉树，但是在现实应用中利用中序+后/前序的方式还原二叉树其实颇为不便（也许手写对于熟练的人来说不算难，但是代码就显得有些麻烦了），所以我们本身不会常用这样的手段。

这样不完美的特性导致了二叉树到的遍历结果是一个单向的映射而非双射，这就为二叉树的存储带来了麻烦，我们必须要考虑一种实现二叉树的合理存储方案。

2.层次遍历实现存储

        我们昨天提到过利用顺序表存储二叉树的冗余性（见此：日撸 Java 三百行（21 天: 二叉树及其基本操作），下面就不再赘述这个方法的内涵），而今天我们要再度审视下这个方案。

       昨天讲这个顺序存储的时候我们省略一些描述的细节，这里补充下：这个方案利用了树的层次遍历思想，首先它将一个二叉树按照其层次将其补为一个完全二叉树，然后按照层次遍历的顺序（逐层按序数，从上层到下层）得到。

        以昨天的图举例，若用链表只需要存储5个元素（这里为了方便，我们暂时不论指针冗余有关的开销），如果我们用顺序表的层次遍历表示就是：
【a b null c null null null null d null null null null null null null null e】，可见一共存储了18个元素，冗余度高达72.2%，不难想，此冗余度会随着“ 结点数与层数比 ”的减少而递增。这是我们昨天的思维，今天我们从存储表示的统一性角度来看。

        这种存储方案是逐层剖离而拼凑成一个顺序表的，而我们只要从根结点开始模仿层次遍历逐步复刻我们的顺序表内容即可（因为是完全二叉树，属于每层的结点的孩子结点能完全对应）因此，这种层次遍历恢复的思想是一种完美的转储材料。但是现在的不足就是冗余度的问题，实际上，我们可利用压缩存储来缩小这种冗余：

'a'	'b'	'c'	'd'	'e'
0	1	3	8	17

        这种方案巧妙忽略了中间的无效字符，直接通过下标记录来反映当前字符在树中的情况；同时这个下标是基于完全二叉树的下标情况，而完全二叉树有一个非常特别的性质：对一个结点，若按照层次遍历序号为其编序，某个结点的标号为i（从0开始），那么他的左孩子下标就为2*i+1（若存在），右孩子下标为2*i+2（若存在），这种特殊性质大家可以结合我的图并且表格明显发现，这种性质可以非常方便我们后续编程。

        综上的压缩存储，对于有n个结点的数，我们转储的空间开销就缩小为2n，这是完全可以接受的范围，而且，从某种意义上来说因为这样的双顺序表格式没有指针，因此其存储效率可能还要略高于普通链表，而且这种方案可以与链表式的二叉树通过层次遍历思想双向转换。

二、链表二叉树转储为顺序表的代码

1.基本初始化与BFS

        先整理下我们可能会用到的数据结构和算法，首先我们需要两个顺序表来提供转储的空间，分别下标记录用的数组，分别是记录树结点的数组。前者没什么特别的，但是后者的话可能要视树形结构的数据项类型而决定，这里我们就创建字符数据即可：

    /**
	 * The values of nodes according to breadth first treversal.
	 */
	char[] valuesArray;

	/**
	 * The indices in the complete binary tree.
	 */
	int[] indicesArray;

         然后就是转储的过程，正如我们之前所言，我们需要利用层次遍历，所以这里就不得不提一嘴树形结构的层次遍历常用套路——广度优先搜索（BFS：Breadth First Search）

        这个方案大体上就是利用一个队列完成中间存储，记录下上次访问过的父级结点，然后后续的遍历依次取出队列中的这些父级结点并依据这些父级结点的子节点进行遍历，又因为队列先进先出的性质，我们访问的顺序总是从左到右的。广度遍历是相对于深度遍历而言的，广度的特点在于同层次的访问结点能一次性尽可能的先访问，而深度的特点在于同个路径的结点先访问，他们具有相同的复杂度但是在处理不同的问题时却能表现出不同的性质。这部分内容我先不作过多的模拟，我们具体再后续的图的数据结构的时候我还会专门说下BFS，今天我们先简单提一下即可，不过多探究BFS的内涵，这里只需要理解的就是BFS的使用过程必须要利用队列最为中间存储，并且全程遍历都已队列的状况为遍历的核心。

2.关于队列的准备

        // Initialize arrays.
		int tempLength = getNumNodes();

		valuesArray = new char[tempLength];
		indicesArray = new int[tempLength];
		int i = 0;

		// Traverse and convert at the same time.
		CircleObjectQueue tempQueue = new CircleObjectQueue();
		tempQueue.enqueue(this);
		CircleIntQueue tempIntQueue = new CircleIntQueue();
		tempIntQueue.enqueue(0);

        这里是基本的初始化：首先获得当前链表树的结点tempLength 并初始化两个转储的数组。而接下来，初始化了BFS需要用到的两个循环队列：记录下标的整型队列，记录链表树的每个结点的类引用的队列。这里为了表示一般性我们使用了Object类的范式编程（ 关于Object类 ）实现类引用的队列声明，这里我就不过多描述这个类的实现细节了，具体与我的这篇博客很像，只不过修改了类型的细节。

        那么问题来了，为什么这个队列要存储链树的引用结点？原因在于BFS的特点：BFS的每次遍历总是取出队列中的元素作为我们下次遍历的父级，我们会查看父级有关的邻边从而补充队列。而查看父级有关的邻边这个操作必须保证父级要有查看邻边的能力，那么，这个能力对于树形结构来说，不就是每个结点的leftChild与rightChild属性吗？所以我们必须用可以保存链表树每个结点类型的队列。

        注意给队列的初始化操作，分别先存放了第一个结点于结点队列，第一个下标于下标队列作为初始化，这是方便我们后续BFS代码的循环。（要明白这里this的含义，this是当前类的引用，可以用this访问当前类属性与方法）当然，单独摆出这个代码的话，这个this显得有些突然，因为我给大家省略了本代码的环境，简单补充下：本代码位于一个函数方法中，这个函数是对昨天博客设计的链表树的类的扩充，这个this是反映的是这个方法所在类所构造的对象，也就链树中的某个结点，因为我们转储的起点是根节点，所以这个操作就是就是认定此结点为根节点并向下层次遍历，从而进行转储。

3.核心代码

        BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
		int tempIndex = tempIntQueue.dequeue();
		while (tempTree != null) {
			valuesArray[i] = tempTree.value;
			indicesArray[i] = tempIndex;
			i++;

			if (tempTree.leftChild != null) {
				tempQueue.enqueue(tempTree.leftChild);
				tempIntQueue.enqueue(tempIndex * 2 + 1);
			} // Of if

			if (tempTree.rightChild != null) {
				tempQueue.enqueue(tempTree.rightChild);
				tempIntQueue.enqueue(tempIndex * 2 + 2);
			} // Of if

			tempTree = (BinaryCharTree) tempQueue.dequeue();
			tempIndex = tempIntQueue.dequeue();
		} // Of while

        这个代码就是BFS的精髓了，当然BFS按照个人习惯有各种写法，有的会用队列是非为空作为循环条件，而有的会用队列当前取出的元素作为循环条件（当队列去不出元素会返回一个非法值，这个非法值也可以被捕获，因此我们也可以认为其是在队空时取出的“元素”）简单描述下我们的过程，BFS可以总结为下面的步骤：

1. 取出队列中的元素作为父级（出队）
2. 父级是否合法？若不合法说明队列已经空，程序结束。若合法，进入下一步
3. 遍历当前与父级相邻的结点，若其合法，将其纳入队列（入队）

        这个三步走中，我们需要引入对于数据的“操作”。可以在第2步到第3步之间加入一个2.5步，执行对于父级的“操作” ，当然这个操作也可以放在第三步，在入队前对子元素进行“操作”。至于这个“操作”是什么就视你的目标而定了，如果是打印结点，那么最终就会得到一个层次遍历结果。

        我的代码中，将“操作” 放到2.5步了，并且“操作” 的内容是转储：将结点引用与下标存放到我们初始化的转储数组中。这个过程中我们不断维护两个队列，其中入队操作会因为“查看父级有关的邻边”的操作不同而不同，如果是结点引用的话，那么父级就是利用leftChild / rightChild属性访问子元素；如果是下标的话，那么父级就是利用i*2+1和i*2+2属性访问子元素（我们上面提到的完全二叉树的特性）

4.完整代码

	/**
	 *********************
	 * Convert the tree to data arrays, including a char array and an int array. The
	 * results are stored in two member variables
	 * 
	 * #see #valuesArray
	 * 
	 * @see #indicesArray
	 *********************
	 */
	public void toDataArrays() {
		// Initialize arrays.
		int tempLength = getNumNodes();

		valuesArray = new char[tempLength];
		indicesArray = new int[tempLength];
		int i = 0;

		// Traverse and convert at the same time.
		CircleObjectQueue tempQueue = new CircleObjectQueue();
		tempQueue.enqueue(this);
		CircleIntQueue tempIntQueue = new CircleIntQueue();
		tempIntQueue.enqueue(0);

		BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
		int tempIndex = tempIntQueue.dequeue();
		while (tempTree != null) {
			valuesArray[i] = tempTree.value;
			indicesArray[i] = tempIndex;
			i++;

			if (tempTree.leftChild != null) {
				tempQueue.enqueue(tempTree.leftChild);
				tempIntQueue.enqueue(tempIndex * 2 + 1);
			} // Of if

			if (tempTree.rightChild != null) {
				tempQueue.enqueue(tempTree.rightChild);
				tempIntQueue.enqueue(tempIndex * 2 + 2);
			} // Of if

			tempTree = (BinaryCharTree) tempQueue.dequeue();
			tempIndex = tempIntQueue.dequeue();
		} // Of while
	}// Of toDataArrays

5.数据模拟

	/**
	 *********************
	 * The entrance of the program.
	 * 
	 * @param args Not used now.
	 *********************
	 */
	public static void main(String args[]) {
		BinaryCharTree tempTree = manualConstructTree();
		System.out.println("\r\nPreorder visit:");
		tempTree.preOrderVisit();
		System.out.println("\r\nIn-order visit:");
		tempTree.inOrderVisit();
		System.out.println("\r\nPost-order visit:");
		tempTree.postOrderVisit();

		System.out.println("\r\n\r\nThe depth is: " + tempTree.getDepth());
		System.out.println("The number of nodes is: " + tempTree.getNumNodes());

		tempTree.toDataArrays();
		System.out.println("The values are: " + Arrays.toString(tempTree.valuesArray));
		System.out.println("The indices are: " + Arrays.toString(tempTree.indicesArray));

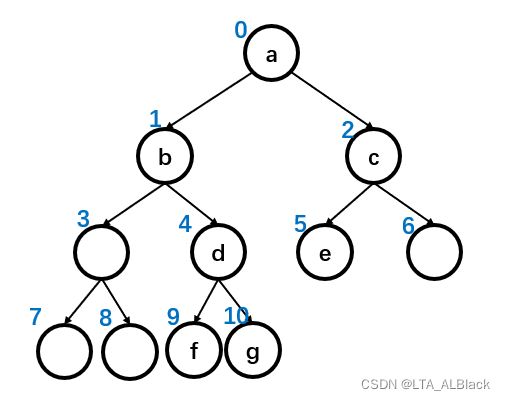
	}// Of main

        我们对于数据的模拟沿用了昨日的数据，基本的树形结构如下：

        若我们按照今日思路，扩充其上层的空节点，并且利用层次遍历标序号，有：

        运行结果如下：（可见与我们绘制的逻辑图完全一致）

 

 总结

        随着学习深入，相关问题越来越抽象，因此我们的数据结构操作开始渐渐侧重步骤的分析，但我还是尽量把原理说清楚。

        数据的转储给我们的感觉是一种对于特殊数据结构的妥协，因为现实中的很多逻辑特性总是复杂的，无论是树形的还是图状的，要想灵活将其体现在一个讲究“顺序至上”的物理存储其中，我们就要尽可能结合已有的各种数据结构对于原来复杂的逻辑结构进行各种 基于某种规则的 可逆的 改造。而对于树形结构的顺序存储思路就是对于树形结构的特殊性而不得已提出的手段，有了转储的可能，我们就可以用任何线性的思维去简化各种树形结构。

        你可能会想：明明昨天都说了链表表示树是最好最直观的，为何今天又在绞尽脑汁想怎么把其最节俭地放到顺序表中？

        我举个例子，计算机数据在内部信道上传播利用的都是数字信号，这些信号通过电气性质定义后可以非常好表示二进制，非常符合我们计算机的思维。但是如果我要把这些数据传到遥远的另一台主机上，我就需要搭上高速远距离信道，而在这些信道上，数字信号是脆弱的，因此我们需要对其进行调制变为具有更强适用性的模拟信号。这里其实是一样的道理，链表树具有非常优良的操作特性，我们可以用链表树完成各种遍历等复杂操作，但是我们却无法用任何一个简单的字符串序列去唯一这棵树（不像线性表）。而转储概念的提出为我们的实现唯一表示树提供的方案，至此，树的表示才真正变得灵活起来。

        这给我们一个提示：若今后想用使用一个数据结构去说明一个逻辑设想，处理考虑操作可行性之外，我们还要多留个心眼，思考我们设计的数据结构是否具有优良的表示特性，否则我们的数据是很难实现各种灵活的转换，这个数据结构就是“偏科”的