《100天一起学习PyTorch》第二天:从零实现线性回归(含详细代码)
PyTorch从零实现线性回归
- ✨本文收录于《100天一起学习PyTorch》专栏,此专栏主要记录如何使用
PyTorch实现深度学习笔记,尽量坚持每周持续更新,欢迎大家订阅! - 个人主页:JoJo的数据分析历险记
- 个人介绍:小编大四统计在读,目前保研到统计学top3高校继续攻读统计研究生
- 如果文章对你有帮助,欢迎✌
关注、点赞、✌收藏、订阅专栏
参考资料:本专栏主要以沐神《动手学深度学习》为学习资料,记录自己的学习笔记,能力有限,如有错误,欢迎大家指正。同时沐神上传了的教学视频和教材,大家可以前往学习。
- 视频:动手学深度学习
- 教材:动手学深度学习
文章目录
- PyTorch从零实现线性回归
- 1.线性回归基本概念
- 2.损失函数
- 3.梯度下降
- 4.Pytorch实现线性回归
-
- 4.1 生成数据集
- 4.2 初始化参数
- 4.3 定义回归模型
- 4.4 计算损失函数
- 4.5 使用梯度下降求解参数
1.线性回归基本概念
线性回归是机器学习中非常常用的模型之一,特别在研究定量数据的问题中,它能分析变量之间的关系,并给出很好的解释。此外,它还是新方法的一个良好起点:许多有趣的统计学习方法可以被视为线性回归的推广或扩展。例如Lasso回归,岭回归,logistic regression,softmax回归。具体理论介绍部分大家可以看我这篇文章:统计学习方法之线性回归详解
简单线性回归模型具体形式可以如下表示:
y = w 1 x 1 + w 2 x 2 + . . . + w n x n + b y = w_1x_1+w_2x_2+...+w_nx_n+b y=w1x1+w2x2+...+wnxn+b
写成向量的形式:
Y = W T X + b Y = W^TX+b Y=WTX+b
在我们拿到一堆数据之后,我们要做就是找到最好的参数 W , b W,b W,b,如何找到最好的参数呢?在那之前我们介绍一下损失函数和梯度下降
2.损失函数
损失函数是衡量一个模型拟合的重要指标,表示实际值和拟合值之间的差距,在线性回归中,损失函数也被称作平方误差函数。我们之所以要求出误差的平方和,是因为一般我们认为误差是非负的,而误差绝对值在求导时不太便利,而误差平方损失函数,对于大多数问题,特别是回归问题,都是一个合理的选择。具体定义如下:
L ( W ^ , b ^ ) = 1 2 m ∑ i = 1 m ( y ( i ) − W T x ( i ) − b ) 2 L(\hat{W},\hat{b})=\frac{1}{2m}\sum_{i=1}^{m}(y^{(i)} - W^Tx^{(i)}-b)^2 L(W^,b^)=2m1i=1∑m(y(i)−WTx(i)−b)2
我们的目标便是选择出可以使得损失函数能够最小的模型参数,因为线性回归是一个很简单的问题,所有大部分情况下都存在解析解,对L求梯度为0的点。为了方便表示,这里我将 b b b也放入到 W W W中,则有:
Y = W T X Y = W^TX Y=WTX
其中, w 0 = b w_0=b w0=b x 0 = 1 x_0=1 x0=1,此时对上述求梯度为0后可以得到正规方程解:
W = ( X T X ) − 1 X T y W = (X^TX)^{-1}X^Ty W=(XTX)−1XTy
3.梯度下降
梯度下降是一种优化算法,后续还会介绍一些其他的优化方法,例如Adam,SGD等。本章暂时用梯度下降来计算参数。梯度下降背后的思想是:开始时我们随机选择一个参数的组合,计算损失函数,然后我们寻找下一个能让损失函数值下降最多的参数组合。
具体公式如下:
w i : = w i − η d L d w i w_{i} := w_i - \eta\frac{dL}{dw_i} wi:=wi−ηdwidL
- 1.初始化一组参数值
- 2.在负梯度方向不断更新参数,其中 η \eta η是学习率,是一个超参数,它决定了我们沿着能让损失函数下降程度最大的方向步长多大,在梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以损失函数的导数。需要我们提前给定。
我们持续这么做直到得到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。此时如何设置合适的 η \eta η值是需要我们考虑的,如果 η \eta η太大,则可能到不了最低点,导致无法收敛,如果 η \eta η太小,那收敛过程太慢,这些细节问题在之后再讨论,接下来我们来看看如何实现一个简单的线性回归模型。
4.Pytorch实现线性回归
导入相关库
import random
import torch
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
4.1 生成数据集
为了方便举例,这里使用模拟数据集进行展示。假设样本来自标准正态分布,每个样本有两个特征,我们生成1000个数据集, w = [ 1 , − 1 ] T w=[1,-1]^T w=[1,−1]T, b = 2 b=2 b=2, ϵ \epsilon ϵ是一个均值为0,标准差为0.1的正态分布
def simulation_data(w,b,n):
X = torch.normal(0,1,(n,len(w)))#生成标准正态分布
y = torch.matmul(X, w)+b#计算回归拟合值
y += torch.normal(0,0.1,y.shape) #加上随机扰动项
return X,y.reshape((-1,1))
true_w = torch.tensor([-1,1],dtype=torch.float32)
true_b = 2
features, target = simulation_data(true_w,true_b,1000)
此时已经生成好了模拟数据集,下面我们绘制图形观察一下
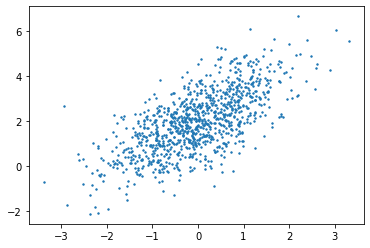
plt.scatter(features[:,(1)].detach().numpy(),target.detach().numpy(),2)
从上图我可以看出,y和一个特征之间的关系呈现明显的线性关系。
4.2 初始化参数
下面我们开始初始化我们要求的参数,通常将 w w w设置为均值为0的正态分布, b b b设置为0向量
w = torch.normal(0,0.1,(2,1),requires_grad=True)
b = torch.zeros(1,requires_grad=True)
4.3 定义回归模型
初始化参数之后,我们下一步就是开始定义我们的线性回归模型
def reg(X,w,b):
return torch.matmul(X,w)+b
4.4 计算损失函数
def loss_fun(y_hat,y):
return(y_hat-y)**2/2/len(y)
4.5 使用梯度下降求解参数
def gd(params,n):
with torch.no_grad():#在外面不需要求解梯度,只有参数更新的时候求参数
for param in params:
param -= n*param.grad#进行梯度下降
param.grad.zero_()#重新将梯度设置为0,这样就不会受到上一次影响
n = 0.01#学习率
num_epochs = 3#训练次数
net = reg
loss = loss_fun
X = features
y = target
for epoch in range(num_epochs):
l = loss(reg(X,w,b),y)#计算损失函数
l.sum().backward()#反向传播求梯度
gd([w,b],n)#更新参数
with torch.no_grad():
train = loss(net(features,w,b),target)
print(f'epoch{epoch+1},loss:{float(train.mean()):f}')
epoch1,loss:0.001797
epoch2,loss:0.001763
epoch3,loss:0.001729
由于本例中是模拟数据集,我们知道真实的参数,因此可以计算出参数估计的误差
print(f'w的误差:{true_w-w.reshape(true_w.shape)}')
print(f'b的误差:{true_b-b}')
w的误差:tensor([-0.8461, 0.8311], grad_fn=)
b的误差:tensor([1.4857], grad_fn=)
大家可以尝试使用其他的学习率,来看一下结果的差异性,一般较常用的是0.01 0.03 0.1 0.3 1
本章的介绍到此介绍,如果文章对你有帮助,请多多点赞、收藏、评论、关注支持!!