如何使用Python构建机器学习模型

　　在构建机器学习模型时，我们希望将误差保持在尽可能低的水平。对于任何打算学习Python进行大数据分析的人来说，这都是一项关键技能。误差的两个主要来源是偏差和方差。如果我们设法减少这两个，那么我们可以建立更准确的模型。

　　但是，我们如何首先诊断偏差和方差?当我们检测到某些东西时应该采取什么行动?

　　在如何使用Python构建机器学习模型中，我们将学习如何使用学习曲线来回答这两个问题。我们将使用现实世界的数据集，并尝试预测电厂的电能输出。

　　假定你对scikit学习和机器学习理论有所了解。如果在我说交叉验证或监督学习时你不皱眉，那么你就很好了。如果你是机器学习的新手，并且从未尝试过scikit，那么如何使用Python构建机器学习模型是一个不错的起点。

　　我们首先简要介绍偏差和方差。

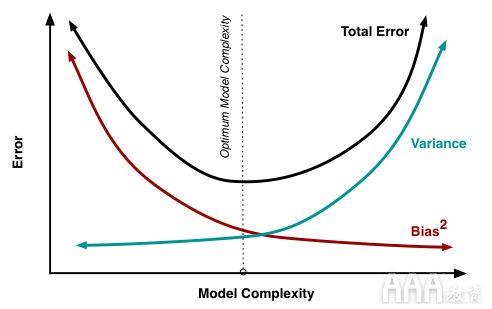
　　偏差方差的权衡

　　在监督学习中，我们假设特征与目标之间存在真实关系，并使用模型估算这种未知关系。如果假设是正确的，那么确实存在一个模型，我们将其称为\(f \)，该模型可以完美描述要素与目标之间的关系。

　　实际上，\(f \)几乎总是完全未知，我们尝试使用模型\(\ hat {f} \)对其进行估计(注意\(f \)和\(\ hat之间的符号略有不同{F}\))。我们使用特定的训练集并获得特定的 \(\ hat {f} \)。如果我们使用不同的训练集，我们很可能会得到不同的\(\ hat {f} \)。随着我们不断更改训练集，我们得到\(\ hat {f} \)的不同输出。\(\ hat {f} \)随着我们更改训练集而变化的量称为方差。

　　要估算真实的\(f \)，我们使用不同的方法，例如线性回归或随机森林。例如，线性回归假设特征和目标之间是线性的。但是，对于大多数现实生活场景而言，要素与目标之间的真实关系非常复杂，而且并非线性关系。简化的假设会使模型产生偏差。关于真实关系的假设越错误，偏差就越大，反之亦然。

　　通常，对某些测试数据进行测试时，模型\(\ hat {f} \)会出现一些错误。从数学上可以证明，偏差和方差都只会增加模型的误差。我们希望误差很小，因此我们需要将偏差和方差保持在最小。但是，这不太可能。偏差和方差之间需要权衡。

　　低偏方法非常适合训练数据。如果我们更改训练集，我们将获得截然不同的模型\(\ hat {f} \)。

　　

 

　　你可以看到，低偏差方法可以捕获不同训练集之间的大多数差异(甚至较小的差异)。\(\ hat {f} \)随我们更改训练集而变化很大，这表明差异很大。

　　方法的偏见程度越小，其数据拟合能力越强。此能力越大，方差越大。因此，偏差越小，方差越大。

　　反之亦成立：偏差越大，方差越小。高偏差方法会建立简单的模型，这些模型通常不适合训练数据。当我们更改训练集时，通常从高偏置算法获得的模型\(\ hat {f} \)彼此之间并没有太大差异。

　　

 

　　如果在更改训练集时\(\ hat {f} \)的变化不大，则方差很小，这证明了我们的观点：偏差越大，方差越小。

　　从数学上讲，很明显为什么我们要低偏差和低方差。如上所述，偏差和方差只会增加模型的误差。但是，从更直观的角度来看，我们希望低偏差以避免构建过于简单的模型。在大多数情况下，简单的模型在训练数据上的表现不佳，并且极有可能在测试数据上重复表现不佳的情况。

　　同样，我们希望方差较小，以避免构建过于复杂的模型。这样的模型几乎完全适合训练集中的所有数据点。但是，训练数据通常包含噪声，仅是来自大量人口的样本。过于复杂的模型会捕获该噪声。当对样本外数据进行测试时，性能通常很差。那是因为模型对样本训练数据的学习太好了。它对某事了解很多，而对其他事情则一无所知。

　　但是实际上，我们需要权衡取舍。我们不能同时拥有低偏见和低方差，因此我们希望瞄准中间的东西。

　　

 

　　当我们在下面生成和解释学习曲线时，我们将尝试为此折衷建立一些实用的直觉。

　　学习曲线–基本思想

　　假设我们有一些数据，并将其分为训练集和验证集。我们从训练集中获取一个实例(是的，一个!)，并使用它来估计模型。然后，我们在验证集和单个训练实例上测量模型的误差。训练实例上的错误将为0，因为完美拟合单个数据点非常容易。但是，验证集上的错误将非常大。

　　这是因为该模型是围绕单个实例构建的，并且几乎可以肯定的是，该模型无法准确地概括以前未见过的数据。现在让我们说，代替一个训练实例，我们取十个并重复误差测量。然后我们需要五十，一百，五百，直到我们使用了整个训练集。当我们更改训练集时，错误分数或多或少会有所不同。因此，我们需要监控两个错误评分：一个用于验证集，一个用于训练集。如果我们绘制两个误差分数随训练集的变化而变化的演变，我们将得到两条曲线。这些称为学习曲线。简而言之，学习曲线显示了错误随着训练集大小的增加而如何变化。

　　下图应帮助你可视化到目前为止描述的过程。在训练集列上，你可以看到我们不断增加训练集的大小。这会导致我们的模型\(\ hat {f} \)稍有变化。在第一行，其中n = 1(n是训练实例的数量)，该模型非常适合单个训练数据点。但是，完全相同的模型非常适合20个不同数据点的验证集。因此，模型的训练集误差为0，而验证集的误差更高。随着我们增加训练集的大小，模型不再能够完美地适合训练集。因此训练误差变得更大。但是，该模型接受了更多数据的训练，因此可以更好地拟合验证集。因此，验证误差减小。提醒你，在所有三种情况下，验证集均保持不变。

　　

 

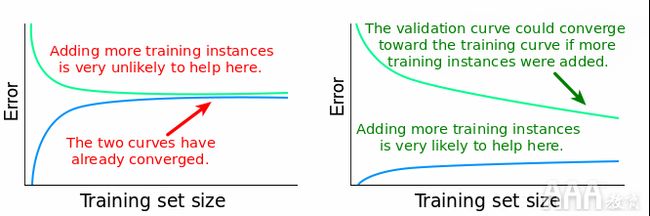
　　如果我们绘制每种训练量的错误分数，我们将获得两条与这些相似的学习曲线：

　　

 

　　学习曲线为我们提供了在监督学习模型中诊断偏差和方差的机会。我们将在接下来的内容中看到这种可能性。

　　数据介绍

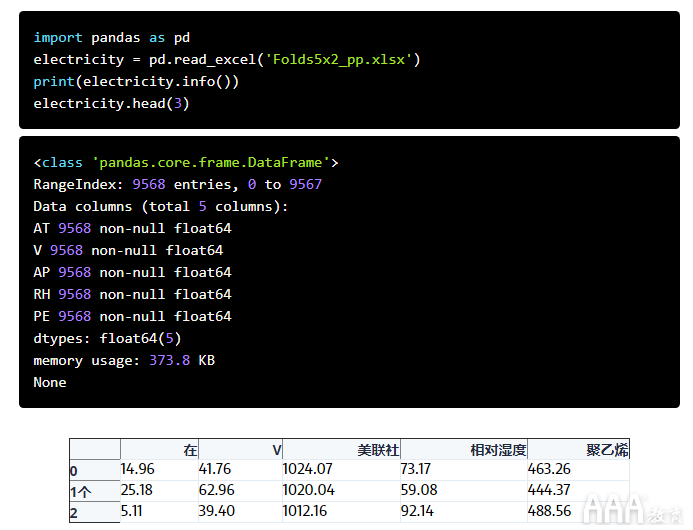
　　上面绘制的学习曲线已理想用于教学目的。但是，实际上，它们通常看起来大不相同。因此，让我们通过使用一些实际数据在实际环境中进行讨论。我们将尝试建立回归模型来预测电厂的每小时电能输出。我们使用的数据来自土耳其研究人员PınarTüfekci和Heysem Kaya，可以从此处下载。由于数据存储在.xlsx文件中，因此我们使用pandas read_excel() 函数读取数据：

　　

 

　　让我们快速解读每个列名称：

　　

 

　　该PE列是目标变量，它描述了每小时的净电能输出。所有其他变量都是潜在特征，每个变量的值实际上是每小时平均值(不是净值，例如PE)。电力由燃气轮机，蒸汽轮机和热回收蒸汽发生器产生。根据数据集的文档，真空度会影响蒸汽轮机，而其他三个变量会影响燃气轮机。因此，我们将在回归模型中使用所有特征列。在这一步中，我们通常会放置一个测试集，彻底探究训练数据，删除任何异常值，测量相关性等。但是，出于教学目的，我们假设已经完成并直接跳出一些学习曲线。在开始之前，需要注意的是没有缺失的值。同样，数字是未缩放的，但我们将避免使用无法缩放数据的模型。

　　确定训练集的大小

　　首先让我们决定我们要用于生成学习曲线的训练集大小。最小值为1。最大值由训练集中的实例数给出。我们的训练集有9568个实例，因此最大值为9568。但是，我们尚未预留验证集。我们将使用80:20的比例进行此操作，最后得到7654个实例的训练集(80%)和1914个实例的验证集(20%)。假设我们的训练集将有7654个实例，则可用于生成学习曲线的最大值为7654。对于我们的情况，在这里，我们使用以下六个大小：

　　

 

　　要意识到的重要一点是，对于每个指定的大小，都会训练一个新模型。如果你正在使用交叉验证(我们将在如何使用Python构建机器学习模型中进行此操作)，则将针对每种训练大小训练k个模型(其中k由用于交叉验证的折叠数给出)。为了节省代码运行时间，最好将自己限制为5至10个培训大小。

　　scikit-learn中的learning_curve()函数

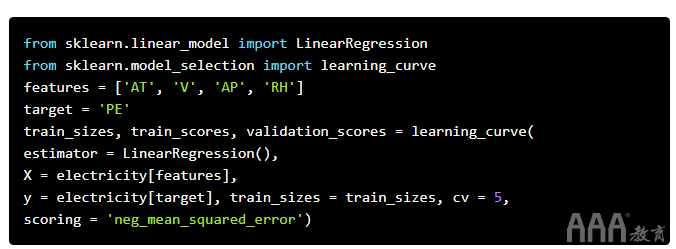
　　我们将使用scikit-learn库中的learning_curve() 函数为回归模型生成学习曲线。我们没有必要将验证集放在一边，因为这learning_curve()会解决这个问题。在下面的代码单元中，我们：

　　1)从进行所需的进口sklearn。

　　2)声明功能和目标。

　　3)使用learning_curve()生成绘制学习曲线所需的数据。该函数返回一个包含三个元素的元组：训练集大小，以及验证集和训练集上的错误分数。在函数内部，我们使用以下参数：

　　a)estimator —表示我们用于估算真实模型的学习算法;

　　b)X —包含要素的数据;

　　c)y —包含目标的数据;

　　d)train_sizes —指定要使用的训练集大小;

　　e)cv —确定交叉验证拆分策略(我们将立即讨论);

　　f)scoring—指示要使用的错误度量;目的是使用均方误差(MSE)度量，但这不是的可能参数scoring;我们将使用最接近的代理服务器(负MSE)，并且稍后只需要翻转标志即可。

　　

 

　　我们已经知道里面有什么train_sizes。让我们检查其他两个变量以查看learning_curve()返回的结果：

　　

 

　　由于我们指定了六个训练集大小，因此你可能希望每种分数都有六个值。相反，我们每行有六行，每行有五个错误分数。发生这种情况是因为learning_curve()在k后台运行了-fold交叉验证，其中的值k由我们为cv参数指定的值给出。在我们的示例中，cv = 5将有五个拆分。对于每个分割，针对指定的每个训练集大小训练一个估计量。上面两个数组中的每一列都指定一个拆分，每一行对应一个测试大小。下表是训练错误分数的表格，可帮助你更好地了解过程：

　　

 

　　要绘制学习曲线，我们只需要每个训练集大小的单个错误评分，而不是5。因此，在下一个代码单元中，我们取每一行的平均值，并翻转错误评分的符号(如前所述)以上)。

　　

 

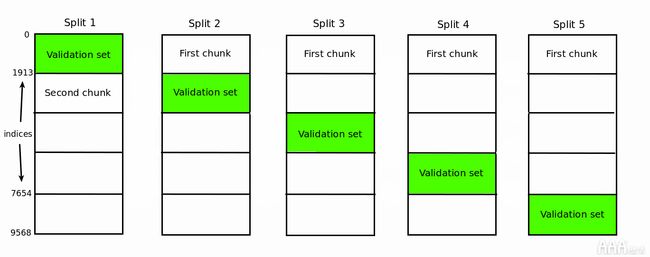
　　现在，我们拥有绘制学习曲线所需的所有数据。但是，在进行绘制之前，我们需要停下来并进行重要观察。你可能已经注意到，训练集上的某些错误分数是相同的。对于对应于训练集大小为1的行，这是预期的，但是其他行呢?除了最后一行，我们有很多相同的值。例如，取第二行，从第二个分割开始，我们具有相同的值。为什么?这是由于未对每个分组随机分配训练数据引起的。让我们借助下图浏览一个示例。当训练大小为500时，将选择训练集中的前500个实例。

　　对于第一次拆分，将从第二个块中获取这500个实例。从第二个分割开始，这500个实例将从第一块中取出。因为我们没有随机化训练集，所以用于第二次分割的500个训练实例是相同的。这说明了从500次训练实例情况的第二次分割开始的相同值。相同的推理适用于100个实例情况，类似的推理适用于其他情况。

　　

 

　　要停止这种行为，我们需要在函数中将shuffle参数设置为。这将使每个分组的训练数据的索引随机化。由于以下两个原因，我们尚未进行随机分组：Truelearning_curve()

　　1)数据经过了五次预混洗(如文档中所述)，因此不再需要随机化。

　　2)我想让你知道这个怪癖，以防你在实践中偶然发现它。

　　最后，让我们作图。

　　学习曲线–高偏差和低方差

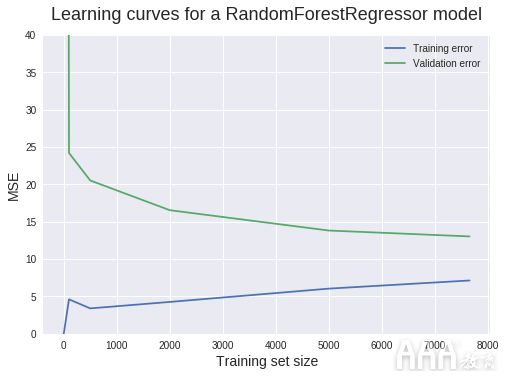
　　我们使用常规的matplotlib工作流程绘制学习曲线：

　　

 

　　

 

　　我们可以从该图中提取很多信息。让我们继续进行。当训练集大小为1时，我们可以看到训练集的MSE为0。这是正常现象，因为该模型完全适合单个数据点时没有问题。因此，当在同一数据点上进行测试时，预测是完美的。但是，当在验证集(具有1914个实例)上进行测试时，MSE会猛增至大约423.4。此相对较高的值是我们将y轴范围限制在0到40之间的原因。这使我们能够精确读取大多数MSE值。预期会有如此之高的价值，因为在单个数据点上训练的模型不太可能能够准确地推广到训练中未见的1914个新实例。当训练集大小增加到100时，训练MSE急剧增加，

　　线性回归模型无法完美预测所有100个训练点，因此训练MSE大于0。但是，由于使用更多数据进行估算，该模型现在在验证集上的表现要好得多。从500个训练数据点开始，验证MSE大致保持不变。这告诉我们一些非常重要的事情：添加更多的训练数据点不会导致明显更好的模型。因此，除了浪费时间(可能是金钱)来收集更多数据之外，我们还需要尝试其他事情，例如切换到可以构建更复杂模型的算法。

　　

 

　　为了避免在这里产生误解，请务必注意，真正无济于事的是向训练数据中添加更多实例(行)。但是，添加更多功能是另一回事，并且很有可能会有所帮助，因为这将增加当前模型的复杂性。现在让我们开始诊断偏差和方差。偏差问题的主要指标是较高的验证误差。在我们的案例中，验证MSE停滞在大约20的值。但是，这有多好?我们将从某些领域的知识(在这种情况下可能是物理或工程学)中受益来回答这个问题，但让我们尝试一下。

　　从技术上讲，该值20具有MW \(^ 2 \)(兆瓦平方)作为单位(当我们计算MSE时，单位也将平方)。但是我们的目标列中的值以MW为单位(根据文档)。取20 MW \(^ 2 \)的平方根可得出大约4.5 MW。每个目标值代表每小时净输出电能。因此，每小时我们的模型平均减少4.5 MW。根据Quora的回答，4.5 MW相当于4500台手持式吹风机产生的热能。如果我们试图预测一天或更长时间的总能量输出，这将加起来。我们可以得出结论，MSE为20 MW \(^ 2 \)很大。因此我们的模型存在偏差问题。

　　但这是低偏差问题还是高偏差问题?为了找到答案，我们需要查看训练错误。如果训练误差非常低，则意味着训练数据非常适合估计模型。如果模型非常适合训练数据，则意味着该模型相对于该组数据具有较低的偏差。如果训练误差高，则意味着估计模型无法很好地拟合训练数据。如果模型不能很好地拟合训练数据，则意味着它对该数据集有很高的偏见。

　　

 

　　在我们的特定情况下，训练的MSE稳定在大约20 MW \(^ 2 \)的值。正如我们已经确定的那样，这是一个很高的错误评分。因为验证MSE高，并且训练MSE也高，所以我们的模型存在高偏差问题。现在让我们开始诊断最终的方差问题。估计方差可以通过至少两种方式完成：

　　1)通过检查验证学习曲线和训练学习曲线之间的差距。

　　2)通过检查训练错误：随着训练集大小的增加，它的价值及其演变。

　　

 

　　狭窄的差距表明低方差。通常，间隙越窄，方差越小。反之亦然：差距越大，差异越大。现在让我们解释为什么会这样。正如我们之前讨论的，如果方差很大，则该模型非常适合训练数据。当训练数据拟合得太好时，模型将难以推广训练中未见的数据。当在训练集上然后在验证集上测试这种模型时，训练误差将很低，并且验证误差通常会很高。随着我们更改训练集大小，这种模式将继续，并且训练和验证错误之间的差异将确定两条学习曲线之间的差距。

　　训练和验证错误之间的关系以及差距可以用以下方式总结：\(差距=验证\错误–训练\错误\)因此，两个错误之间的差异越大，差距就越大。差距越大，差异越大。在我们的情况下，差距非常狭窄，因此我们可以安全地得出结论，方差很小。训练有素的 MSE分数高也是检测低方差的快速方法。如果学习算法的方差很小，那么当我们更改训练集时，该算法将提供简单且相似的模型。由于模型过于简单，他们甚至不能满足训练数据以及(他们underfit数据)。因此，我们应该期待训练有素的MSE。因此，训练有素的MSE可用作低方差的指标。

　　

 

　　在我们的案例中，MSE训练的高峰期约为20，而我们已经得出结论，这是很高的价值。因此，除了狭窄的差距之外，我们现在还有另一个确认，那就是我们有一个低方差问题。到目前为止，我们可以得出以下结论：

　　1)我们的学习算法存在高偏差和低方差的问题，不适合训练数据。

　　2)在当前的学习算法下，向训练数据中添加更多实例(行)的可能性极小，无法导致更好的模型。

　　此时的一种解决方案是更改为更复杂的学习算法。这将减少偏差并增加方差。一个错误是尝试增加训练实例的数量。通常，在解决高偏差和低方差问题时，这两个其他修复程序也起作用：

　　1)在更多特征上训练当前的学习算法(为避免收集新数据，你可以轻松生成多项式特征)。这应该通过增加模型的复杂性来降低偏差。

　　2)如果是这样的话，请 减少当前学习算法的规则化。简而言之，正则化会阻止算法很好地拟合训练数据。如果减少正则化，则该模型将更好地拟合训练数据，结果，方差将增加且偏差将减小。

　　学习曲线–低偏差和高方差

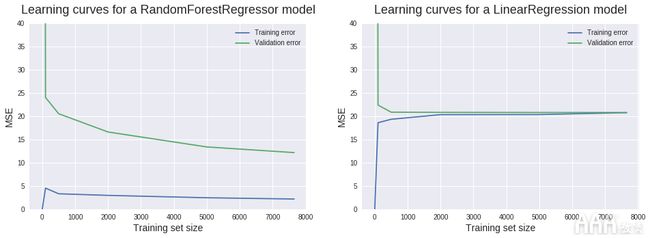
　　让我们看看这里的非正规随机森林回归器的价格。我们将使用与上述相同的工作流程来生成学习曲线。这次，我们将所有内容捆绑到一个函数中，以便以后使用。为了进行比较，我们还将显示上面的线性回归模型的学习曲线。

　　

 

　　

 

　　现在，让我们尝试应用刚刚学到的知识。最好暂时停止阅读，然后尝试自己解释新的学习曲线。查看验证曲线，我们可以看到我们已经减少了偏差。仍然存在一些明显的偏见，但没有以前那么多。观察训练曲线，我们可以推断出这次存在一个低偏差问题。

　　两条学习曲线之间的新差距表明方差显着增加。低训练水平的MSE证实了这种高方差的诊断。较大的差距和较低的训练误差也表示过度拟合的问题。当模型在训练集上表现良好但在测试(或验证)集上表现较差时，就会发生过度拟合。我们在这里可以得出的一个更重要的观察结果是，添加新的训练实例很可能会产生更好的模型。验证曲线不会稳定在所使用的最大训练集大小上。它仍然有可能减小并收敛到训练曲线，类似于我们在线性回归情况下看到的收敛。到目前为止，我们可以得出以下结论：

　　1)我们的学习算法(随机森林)具有较高的方差和相当低的偏差，因此过度拟合了训练数据。

　　2)在当前的学习算法下，添加更多的训练实例很可能会导致更好的模型。

　　在这一点上，我们可以做一些事情来改善我们的模型：

　　1)添加更多的训练实例。

　　2)增加我们当前学习算法的正则化。这将减少方差并增加偏差。

　　3)减少我们当前使用的训练数据中的特征数量。该算法仍将很好地拟合训练数据，但是由于特征数量的减少，它将建立较简单的模型。这将增加偏差并减小方差。

　　在我们的情况下，我们没有任何其他随时可用的数据。我们可以去电厂进行一些测量，但是我们将其保存在另一个帖子中(只是在开玩笑)。让我们尝试规范化我们的随机森林算法。一种方法是调整每个决策树中叶节点的最大数量。这可以通过使用max_leaf_nodes参数来完成RandomForestRegressor()。你不一定必须了解这种正则化技术。对于我们这里的目的，你需要关注的是这种正则化对学习曲线的影响。

　　

 

　　

 

　　不错!差距现在更窄了，因此变化也更少了。偏见似乎有所增加，这就是我们想要的。但是我们的工作还远远没有结束!验证的MSE仍显示出很大的降低潜力。你可以为实现该目标而采取的一些步骤包括：

　　1)添加更多的训练实例。

　　2)添加更多功能。

　　3)功能选择。

　　4)超参数优化。

　　理想的学习曲线和不可减少的误差

　　学习曲线是在机器学习工作流程的每个点快速检查我们的模型的好工具。但是我们怎么知道什么时候停止?我们如何识别完美的学习曲线?对于我们之前的回归案例，你可能会认为理想的情况是两条曲线都朝着MSE 0收敛。这确实是理想的情况，但不幸的是，这是不可能的。既没有实践，也没有理论。这是由于某种不可减少的错误。当我们构建模型以映射特征\(X \)与目标\(Y \)之间的关系时，我们假设首先存在这种关系。

　　如果假设为真，则存在一个真实模型\(f \)，该模型完美地描述了\(X \)和\(Y \)之间的关系，如下所示：

　　$$

　　Y = F(X)+束缚\错误\标签{1}

　　$$

　　但是为什么会有错误呢?我们不是刚刚说\(f \)完美地描述了X和Y之间的关系吗?出现错误是因为\(Y \)不仅是我们有限数量的功能\(X \)的函数。可能还有许多其他因素会影响\(Y \)的值。我们没有的功能。\(X \)也可能包含测量错误。因此，除了\(X \)，\(Y \)也是\(irreducible \ error \)的函数。现在，让我们解释一下为什么该错误是不可减少的。当我们使用模型\(\ hat {f}(X)\)估算\(f(X)\)时，我们引入了另一种误差，称为可归约误差：

　　$$

　　f(X)= \ hat {f}(X)+可归约\错误\ tag {2}

　　$$

　　将\(f(X)\)替换为\((1)\)，我们得到：

　　$

　　Y = \ hat {f}(X)+可归约\错误+不可约\错误\ tag {3}

　　$$

　　通过建立更好的模型可以减少可减少的误差。查看方程\((2)\)我们可以看到，如果\(reducible \ error \)为0，则我们的估计模型\(\ hat {f}(X)\)等于真实模型\(f (X)\)。

　　但是，从\((3)\)可以看出，即使\(reducible \ error \)为0，方程中也仍然存在\(irreducible \ error \)。由此得出的结论是，无论模型估算值多么好， ，通常仍然存在一些我们无法减少的错误。这就是为什么这个错误被认为是不可减少的。这告诉我们，在实践中，我们可以看到的最佳学习曲线是收敛于某些不可减少误差的值，而不是收敛于某些理想误差值的曲线(对于MSE，理想误差分数为0;我们将立即看到其他错误指标具有不同的理想错误

　　

 

　　实际上，不可减少误差的确切值几乎总是未知的。我们还假设不可约误差与\(X \)无关。这意味着我们不能使用\(X \)来找到真正的不可约错误。用更精确的数学语言表达同一件事，没有函数\(g \)映射\(X \)到不可约误差的真实值：

　　$$

　　不可约\错误\ neq g(X)

　　$$

　　因此，无法根据我们拥有的数据知道不可减少误差的真实值。在实践中，一个好的解决方法是尝试尽可能降低错误分数，同时要记住，限制是由一些不可减少的错误所给定的。

　　那分类呢?

　　到目前为止，我们已经了解了在回归设置中学习曲线的知识。对于分类任务，工作流程几乎相同。主要区别在于，我们将不得不选择另一种错误度量标准-一种适合评估分类器性能的度量标准。让我们来看一个例子：

　　

 

　　与到目前为止我们所看到的不同，请注意，训练错误的学习曲线高于验证错误的学习曲线。这是因为所使用的分数(准确性)描述了模型的良好程度。精度越高，越好。另一方面，MSE描述了模型的严重程度。MSE越低越好。这对于不可减少的错误也有影响。对于描述模型有多糟糕的错误度量标准，不可减少的错误给出了一个下限：你不能低于这个范围。对于描述模型的好坏的度量指标，不可减少的误差给出了一个上限：你无法获得更高的误差。在此附带说明，在更多的技术著作中，术语贝叶斯错误率通常用于指代分类器的最佳错误评分。这个概念类似于不可减少的误差。

　　下一步

　　学习曲线构成了一种在任何监督学习算法中诊断偏差和方差的好工具。我们已经学习了如何使用scikit-learn和matplotlib生成它们，以及如何使用它们来诊断模型中的偏差和方差。为了巩固你所学的内容，请考虑以下一些步骤：

　　1)使用不同的数据集为回归任务生成学习曲线。

　　2)生成分类任务的学习曲线。

　　3)通过从头开始编写所有内容来生成监督学习任务的学习曲线(请勿learning_curve()从scikit-learn中使用)。使用交叉验证是可选的。

　　4)将没有交叉验证的学习曲线与使用交叉验证的曲线进行比较。两种曲线应用于相同的学习算法。

 

摘自：https://www.aaa-cg.com.cn/data/2746.html