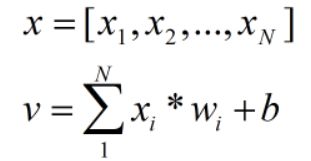机器学习——神经网络（三）：线性神经网络

线性神经网络（LMS）

1.基础理论

• 对比理解：

感知器	LMS
只有两种输出（1或者-1）	输出可以是任意的值
激活函数可以是sign、sigmod等函数	激活函数是线性函数
解决不了异或等问题	只能解决线性可分问题，但是可以解决异或问题

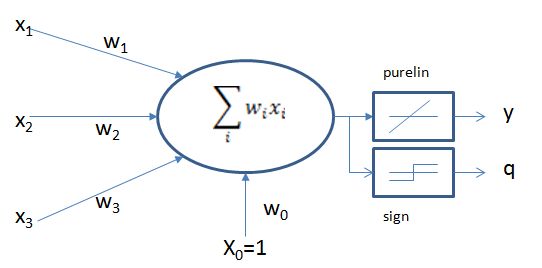
• 网络结构：

>

• LMS学习算法（最小均方误差算法）：LMS与感知器都是基于纠错学习规则的方法，但是LMS更容易实现，也称之为$\delta$规则
  $$e(n)=d(n)-x^T(n)\omega (n)$$
  采用均方误差作为评价标准$$mse=\frac{1}{Q}\sum _{k=1}^Q(e^2(k))$$
  其中Q是训练样本的个数，线性网络学习的目标是找到合适的w使得误差的均方误差最小，只要mse对w求偏导数，再令偏导数等于0就可以求出mse的极值。

1. 为什么用两个激活函数：

• 如上图所示在运算的过程中同时运用了两个激活函数purelin函数和sign函数
• 通常在训练的时候使用purelin函数，在训练完成后需要输出的时候使用sign函数
• 其中的原因在于：使用线性函数得到的结果是所有的值都有可能存在的，但是输出的标签只有两个，所以需要通过sign函数进行整合

2. Delta 学习规则：利用梯度下降法的一般性学习规则

• 梯度下降可以参考梯度下降算法原理讲解——机器学习

• 计算推导：

X是指输入神经元
v是指输出神经元

2. 简单的线性神经网络例子:

说明

1. 数据点为（3,3）、（4,3）、（1，1），其中（3,3）和（4,3）为正样本（1,1）为负样本
2. 初始化权值的范围在[-1,1]

import numpy as np
import matplotlib.pyplot as plt
# 载入数据
x_data = np.array([[1,3,3],
                   [1,4,3],
                   [1,1,1]])
y_data = np.array([[1,1,-1]])

# 设置权值
w = (np.random.random(3)-0.5)*2
print(w)

# 设置学习率
lr = 0.11
# 神经网络的输出
out_data = 0
# 统计迭代次数
n = 0

def update():
    global x_data,y_data,w,lr,n
    n += 1
    out_data = np.dot(x_data,w.T) # x_data是4*3矩阵，w是3*1矩阵,输出4*1矩阵
    w_c = lr*((y_data-out_data.T).dot(x_data))/int(x_data.shape[0])# 分母求得误差的总合，分子表示sample的数量，结果表示平均误差
    w = w+w_c
 for i in range(100):
    update() # 权值更新
    out_data = np.sign(np.dot(x_data,w.T)) # 计算当前输出
    print("epoch:",i)
    print("w:",w)
    if(out_data==y_data.T).all():     # 如果当前输出与实际输出相当，模型收敛，循环结束（。all是全部相等的意思）
        print("#####################")
        print("finished")
        print("epoch:",i)
        print("#####################")
        break
# 正样本
x1 = [3,4]
y1 = [3,3]
# 负样本
x2 = [1]
y2 = [1]

# 计算分界线的斜率以及截距
k = -w[0,1]/w[0,2]
b = -w[0,0]/w[0,2]
print("k = ",k)
print("b = ",b)

xdata =np.linspace(0,5)
plt.figure()
plt.plot(xdata,xdata*k+b,'r')
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='y')
plt.show()

结果：

3.使用线性神经网络解决异或问题：

用一种简介的方式解决线性不可分的问题：用多个线性函数对区域进行划分，然后对各个神经元的输出做逻辑运算
解决异或问题需要利用曲线，所以构建跟多的输入属性即

$(1,x_1,x_2,x_1^2,x_2^2,2x_1{x}_2)$

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
# 载入数据(直接构建)
x_data = np.array([[1,0,0,0,0,0],
                   [1,0,1,0,0,1],
                   [1,1,0,1,0,0],
                   [1,1,1,1,1,1]])
y_data = np.array([[-1,1,1,-1]])

# 使用sklearn中的PolynomialFeatures函数生成
poly_reg = PolynomialFeatures(degree=2)
x_poly = poly_reg.fit_transform([[0,0],
                                [0,1],
                                [1,0],
                                [1,1]])
print(x_poly)
# 标签
y_data = np.array([[-1,1,1,-1]])
# 设置权值
w = (np.random.random(6)-0.5)*2
print(w)
# 设置学习率
lr = 0.11
# 神经网络的输出
out_data = 0
# 统计迭代次数
n = 0

def update():
    global x_data,y_data,w,lr,n
    n += 1
    out_data = np.dot(x_data,w.T) # x_data是4*3矩阵，w是3*1矩阵,输出4*1矩阵
    w_c = lr*((y_data-out_data.T).dot(x_data))/int(x_data.shape[0])# 分母求得误差的总合，分子表示sample的数量，结果表示平均误差
    w = w+w_c
for i in range(1000):
    update() # 权值更新
# 正样本
x1 = [0,1]
y1 = [1,0]
# 负样本
x2 = [1,0]
y2 = [1,0]

def calculate(x,root):
    """进行公式推导，确定二次方程的解得到a/b/c返回函数的解"""
    a = w[0,5]
    b = w[0,2]+x*w[0,4]
    c = w[0,0]+x*w[0,1]+x*x*w[0,3]
    if root ==1:
        return(-b+np.sqrt(b*b-4*a*c))/(2*a)
    if root == 2:
        return(-b-np.sqrt(b*b-4*a*c))/(2*a)
# 绘图
xdata =np.linspace(-1,2) # linspace是线性划分区间，生成一系列的点
plt.figure()
plt.plot(xdata,calculate(xdata,1),'r')
plt.plot(xdata,calculate(xdata,2),'r')
plt.plot(x1,y1,'bo') # 注意这里的plot并非是scatter
plt.plot(x2,y2,'yo')
plt.show()

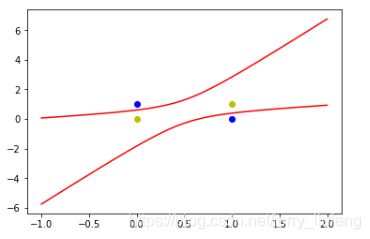
结果视图：

进击的巨人——三笠.阿克曼