k近邻算法总结

k近邻法（k-nearest neighbor, k-NN）是一种基本分类与回归方法。本文先从机器学习的角度探讨分类和回归问题中的 k 近邻法，然后再将其延申到图像分类的计算机视觉场景中，希望能对大家有所帮助。

---

k-近邻算法(KNN)

• 概念：

k-近邻算法（K Nearest Neighbor）又叫KNN算法，这个算法是机器学习里面一个经典基础算法，易于理解，是小白了解机器学习的很好例子。

• 定义：

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

• 简介：

k 近邻法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。k 近邻算法假设给定一个训练数据集，其中的实例类别已确定。分类时，对新的实例，根据其k个最近邻的训练实例的类别，通过多数表决等方式进行预测。
因此，在学习掌握k近邻算法时，主要关注模型及其三要素：距离度量、k 值选择和分类决策规则。
本文先介绍k近邻算法模型，然后讨论k近邻算法的模型及三个基本要素，最后以python代码实现讲述k近邻算法的实现方法。

这么说可能还是很模糊，接下来看详细介绍

---

k-近邻三个基本要素

k 近邻算法中，当训练集、距离度量（如欧氏距离）、k值及分类决策规则（如多数表决）确定后，对于任何一个新的输入实例，它所属的类唯一确定。

距离度量

距离就是平面上两个点的直线距离。

关于距离的度量方法，常用的有：欧几里得距离、余弦值（cos）, 相关度 （correlation）, 曼哈顿距离 （Manhattan distance）或其他。
距离的选择有很多种，常用的距离函数如下：

1. 明考斯基(Minkowsky)距离

$$d(X,Y)=[\sum _{i=1}^n|x_i-y_i{|}^{\lambda }{]}^{\frac{1}{\lambda }}$$
λ一般取整数值，不同的λ取值对应于不同的距离。

2. 曼哈顿(Manhattan)距离

$$d(X,Y)=\sum _{i=1}^n|x_i-y_i|$$
该距离是Minkowsky距离在λ=1时的一个特例。

3. Cityblock距离

$$d(X,Y)=\sum _{i=1}^n{w}_i|x_i-y_i|$$
该距离是Manhattan距离的加权修正，其中wi,i=1,2,…,n是权重因子。

4. 欧几里德(Euclidean)距离（欧氏距离）

$$d(X,Y)=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$
欧氏距离是Minkowsky距离在λ=2时的特例。

5. Canberra距离

$$d(X,Y)=\sum _{i=1}^n(x_i-y_i)(x_i+y_i)$$

6. Mahalanobis距离(马式距离)

$$d(X,M)=\sqrt{(X-M{)}^T\sum ^{-1}(X-M)}$$
d(X,M)给出了特征空间中的点X和M之间的一种距离测度，其中M为某一个模式类别的均值向量，∑为相应模式类别的协方差矩阵。 该距离测度考虑了以M为代表的模式类别在特征空间中的总体分布,能够缓解由于属性的线性组合带来的距离失真。易见，到M的马式距离为常数的点组成特征空间中的一个超椭球面。

7. 切比雪夫(Chebyshev)距离

$$d(X,Y)=max(|x_i-y_i|)$$

$$L_{\infty }=(\underset{k\to \infty }{\lim }\sum _{i=1}^k|x_i-y_i{|}^k{)}^{\frac{1}{k}}$$
切比雪夫距离或是L∞度量是向量空间中的一种度量，二个点之间的距离定义为其各坐标数值差的最大值。在二维空间中。以(x1,y1)和(x2,y2)二点为例，其切比雪夫距离为：
$$d=max(|x_2-x_1|,|y_2-y_1|)$$

8. 平均距离

$$d_{average}=[\sum _{i=1}^n|x_i-y_i{|}^2{]}^{\frac{1}{2}}$$

k值选择

K：近邻数，即在预测目标点时取几个相邻的点来预测。
K值得选取非常重要，因为：

• 如果当K的取值过小时，一旦有噪声得成分存在们将会对预测产生比较大影响，例如取K值为1时，一旦最近的一个点是噪声，那么就会出现偏差，K值的减小就意味着整体模型变得复杂，容易发生过拟合；
• 如果K的值取的过大时，就相当于用较大邻域中的训练实例进行预测，学习的近似误差会增大。这时与输入目标点较远实例也会对预测起作用，使预测发生错误。K值的增大就意味着整体的模型变得简单；
• 如果K=N的时候，那么就是取全部的实例，即为取实例中某分类下最多的点，就对预测没有什么实际的意义了；

K 的取值尽量要取奇数，以保证在计算结果最后会产生一个较多的类别，如果取偶数可能会产生相等的情况，不利于预测。

K 的取法：

• 常用的方法是从k=1开始，使用检验集估计分类器的误差率。重复该过程，每次K增值1，允许增加一个近邻。选取产生最小误差率的K。

• 一般k的取值不超过20，上限是n的开方，随着数据集的增大，K的值也要增大。

分类决策规则

k近邻算法中的分类决策规则往往是多数表决，即由输入实例的k个近邻的训练实例中的多数类决定输入实例的类。通俗地理解，即少数服从多数。
多数表决规则（majority voting rule） 有如下解释：如果分类的损失函数为0-1损失函数，分类函数为
$$f:R^n\to c_1,c_2,...,c_k$$
那么误分类的概率是
$$P(Y\ne f(X))=1-P(Y=f(X))$$
对给定的实例 x∊X，其最近邻的k个训练实例点构成集合：$$N_k(x)。$$如果涵盖Nk(x)的区域的类别是cj​，那么误分类率是：
$$\frac{1}{k}\sum _{x_i\in N_k(x)}I(y_i\ne c_j)=1-\frac{1}{k}\sum _{x_i\in N_k(x)}I(y_i=c_j)$$

要使误分类率最小即经验风险最小，就要使$$\sum _{x_i\in N_k(x)}I(y_i=c_j)$$ 最大，所以多数表决规则等价于经验风险最小化。

例如：
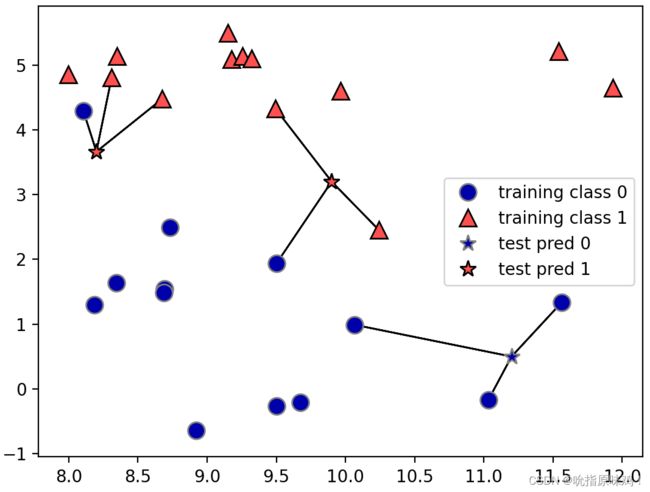
下面的例子中共有两种类别：圆形、三角形，现有三个未知类别的数据点（五角星的点），需要对其进行分类。首先考虑一个近邻的情况，如下图所示，两个未知数据点被归为类别0，一个未知数据点被归为类别1。

在考虑多邻居情况时，我们用“投票法”来指定标签。也就是说，对于每个测试点，我们数一数多少个邻居属于类别0，多少个邻居属于类别1，然后将出现次数更多的类别作为预测结果。
如下图所示是三个近邻的分类情况，其中两个未知数据点被归为类别1，一个未知数据点被归为类别0。

以上就是k近邻算法的基本介绍，接下来将使用python中的sklearn模块举例说明k近邻算法的使用用法。

---

应用一：k近邻分类

举例

step1. 首先将数据分为训练集和测试集

from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

step2. 导入类并将其实例化。
这时可以设定参数，比如邻居个数。

from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)

step3. 现在，利用训练集对这个分类器进行拟合。
对于KNeighborsClassifier来说就是保存数据集，以便在预测时计算与邻居之间的距离。

clf.fit(X_train, y_train)

step4. 调用predict方法来对测试数据进行预测。
对于测试集中的每个数据点，都要计算它在训练集的最近邻，然后找出其中出现次数最多的类别。

print("Test set prediction:{}".format(clf.predict(X_test)))
# 输出：Test set prediction:[1 0 1 0 1 0 0]

step5. 为了评估模型的泛化能力的好坏，我们可以对测试数据和测试标签调用score方法。

print("Test set accuracy:{:.2f}".format(clf.score(X_test, y_test)))
# 输出：Test set accuracy:0.86

分析

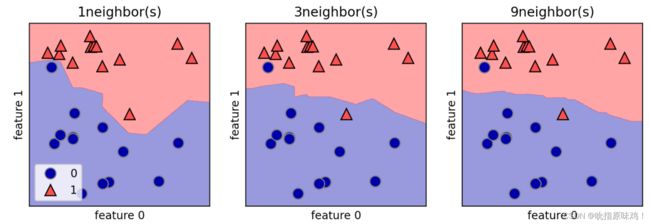
对于二维数据集，我们还可以在xy平面上画出所有可能的测试点的预测结果。我们根据平面中每个点所属的类别对平面进行着色。这样可以查看决策边界，即算法对类别0和类别1的分界线。

# 分别将1个、3个、9个邻居三种情况的决策边界可视化
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(10, 3))

for n_neighbors, ax in zip([1, 3, 9], axes):
    # fit方法返回对象本身，所以我们可以将实例化和拟合放在一行代码中。
    clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
    mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
    mglearn.discrete_scatter(X[:,0], X[:,1], y, ax=ax)
    ax.set_title("{}neighbor(s)".format(n_neighbors))
    ax.set_xlabel("feature 0")
    ax.set_ylabel("feature 1")
axes[0].legend(loc=3)

得到图片：

从上图可以看出，使用单一邻居绘制的决策边界紧跟着训练数据。随着邻居个数越来越多，决策边界也越来越光滑。更平滑的边界对应更简单的模型。

我们研究一下能否证实之前讨论过的模型复杂度和泛化能力之间的关系。我们将在现实世界的乳腺癌数据集上进行研究。先将数据集分成训练集和测试集，然后用不同的邻居个数对训练集和测试集的性能进行评估。

import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=66)

training_accuracy = []
test_accuracy = []
# n_neighbors取值从1到10
neighbors_settings = range(1, 11)

for n_neighbors in neighbors_settings:
    # 构建模型
    clf = KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X_train, y_train)
    # 记录训练集精度
    training_accuracy.append(clf.score(X_train, y_train))
    # 记录泛化精度
    test_accuracy.append(clf.score(X_test, y_test))

plt.plot(neighbors_settings, training_accuracy, label='training accuracy')
plt.plot(neighbors_settings, test_accuracy, label='text accuracy')
plt.ylabel("Accuracy")
plt.xlabel("n_neighbours")
plt.legend()
plt.show()

仅考虑单一近邻时，训练集上的预测结果十分完美。但随着邻居个数的增多，模型变得更简单，训练集精度也随之下降。单一邻居时的测试精度比使用更多邻居时要低，这表示单一近邻的模型过于复杂。与之相反，当考虑10个邻居时，模型又过于简单，性能甚至变得更差。最佳性能在中间的某处，邻居个数大约为6。

---

应用二：k近邻回归

举例

用于回归的k近邻算法在scikit-learn的KNeighborsRegressor类中实现。其用法与KNeighborsClassifier类似。

import mglearn
from sklearn.neighbors import KNeighborsRegressor

X, y = mglearn.datasets.make_wave(n_samples=40)

# 将wave数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# 模型实例化，并将邻居个数设为3
reg = KNeighborsRegressor(n_neighbors=3)
# 利用训练数据和训练目标值来拟合模型
reg.fit(X_train, y_train)

现在可以对测试集进行预测。

print("Test set predictions:\n{}".format(reg.predict(X_test)))
# 输出：Test set predictions:
# [-0.054  0.357  1.137 -1.894 -1.139 -1.631  0.357  0.912 -0.447 -1.139]

我们还可以用score方法来评估模型，对于回归问题，这一方法返回的是R^2分数。
R^2分数也叫做决定系数，是回归模型预测的优度度量，位于0到1之间。等于1对应完美预测，等于0对应常数模型，即总是预测训练集响应的平均值。

print("Test set R^2:{:.2f}".format(reg.score(X_test, y_test)))
# 输出：Test set R^2:0.83

分析

对于我们的一维数据集，可以查看所有特征值对应的预测结果。为了便于绘图，我们创建一个由许多点组成的测试数据集。

import matplotlib.pyplot as plt

fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# 创建1000个数据点，在-3和3之间均匀分布
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
    # 利用1个、3个或9个邻居分别进行预测
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train, y_train)
    ax.plot(line, reg.predict(line))
    ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
    ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
    ax.set_title(
        "{} neighbor(s)\n train score:{:.2f} test score:{:.2f}".format(
            n_neighbors, reg.score(X_train, y_train),
            reg.score(X_test, y_test)))
    ax.set_xlabel("Feature")
    ax.set_ylabel("Target")
axes[0].legend(["Model predictions", "Training data/target",
                "Test data/target"], loc="best")

得到图片：

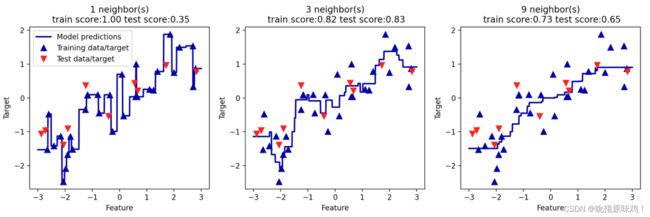
从图中可以看出，仅使用单一邻居，训练集中的每个点都对预测结果有显著影响，预测结果的图像经过所有数据点。这导致预测结果非常不稳定。考虑更多的邻居之后，预测结果变得更加平滑，但对训练数据的拟合也不好。

---

应用三：k近邻图像分类（mnist手写数字识别）

mnist简介

关于MNIST数据集，大部分同学一定不会陌生，它是一个手写数字数据集，包含了0 ~ 9这10个数字，一共有7万张灰度图像，其中6w张训练接，1w张测试集，并且每张都有标签，如标签0对应图像中数字0，标签1对应图像中数字1，以此类推…。 另外，在 MNIST 数据集中的每张图片由 28 x 28 个像素点构成, 每个像素点用一个灰度值表示,灰度值在0 ~ 1 或 0 ~ 255之间，MINIST数据集图像示例如下：

基本流程

1. 收集数据：提供文本文件。
2. 准备数据：编写函数img2vector(),将图像格式转化为分类器使用的向量格式。
3. 分析数据：在python命令行中检查数据，确保它符合要求。
4. 训练模型：使用K近邻算法训练模型。
5. 测试模型：编写函数使用提供的部分数据集作为测试样本。测试样本和非测试样本的区别在于：测试样本是已经完成分类的数据，如果预测分类与实际类别不同，则标记为一个错误。
6. 使用算法：本例没有此步骤，若你感兴趣你可以用此算法去完成 kaggle 上的 Digital Recognition（数字识别）题目。

具体实现

step1. 准备数据：将图像转化为测试向量
转化函数代码：

"""
手写数据集 准备数据：将图像转换为测试向量
"""
def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0, 32*i+j] = int(lineStr[j])
    #返回数组
    return returnVect
#测试函数
testVector = img2vector('testDigits/0_13.txt')
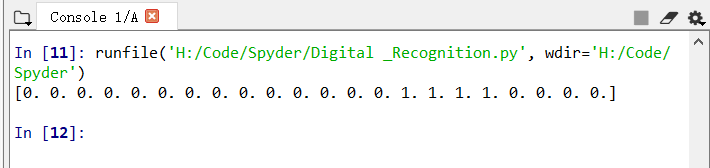
print(testVector[0,0:22])

执行结果如图所示：

step2. 测试算法：使用k近邻算法识别手写数字
测试结果如图所示：

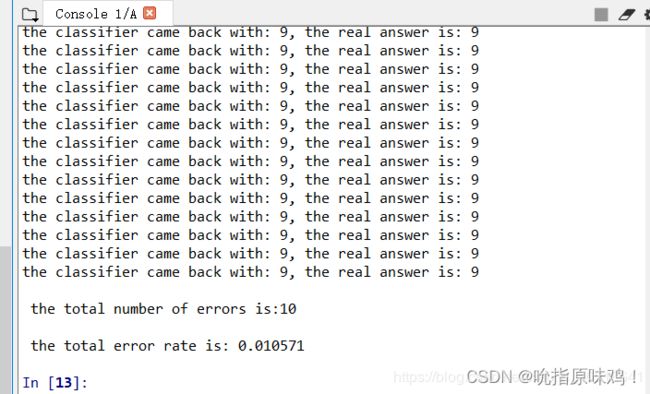
错误率为1.2%

---

总结

1. k近邻法是基本且简单的分类与回归方法。k近邻法的基本做法是：对给定的训练实例点和输入实例点，首先确定输入实例点的k个最近邻训练实例点，然后利用这k个训练实例点的类的多数来预测输入实例点的类。
2. k近邻模型对应于基于训练数据集对特征空间的一个划分。k近邻法中，当训练集、距离度量、k值及分类决策规则确定后，其结果唯一确定。
3. k近邻法三要素：距离度量、邻居个数k值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的pL距离。k值小时，k近邻模型更复杂；k值大时，k近邻模型更简单。k值的选择反映了对近似误差与估计误差之间的权衡，通常由交叉验证选择最优的k。常用的分类决策规则是多数表决，对应于经验风险最小化。在实践中，使用较小的邻居个数（比如3个或5个）往往可以得到比较好的结果。
4. k近邻的优点之一就是模型很容易理解，通常不需要过多调节就可以得到不错的性能。构建最近邻模型的速度通常很快，但如果训练集很大，预测速度可能会比较慢。使用k近邻算法时，对数据进行预处理是很重要的。
5. 虽然k近邻算法很容易理解，但由于预测速度慢且不能处理具有很多特征的数据集，所以在实践中往往不会用到。