PyTorch学习笔记6——模型细节学习

在卷积神经网络中，参考书籍介绍了LeNet, AlexNet, VGG, NiN, GoogleNet, ResNet, DenseNet等网络

6.1批量归一化

6.1.1 批量归一化（batch mormalization）

批量归一化应用于单个可选层（也可以应用到所有层），其原理如下：在每次训练迭代中，我们首先归一化输入，即通过减去其均值并除以其标准差，其中两者均基于当前小批量处理。 接下来，我们应用比例系数和比例偏移。 正是由于这个基于批量统计的标准化，才有了批量归一化的名称。

使用批量归一化层的原因：利用小批量的均值和标准差，不断调整神经网络中间输出，从而使整个神经网络在各层的中间输出的数值更稳定。

6.1.2 从零创建批量归一化层

import torch
from torch import nn, optim
import torch.nn.functional as F

import time

import sys
sys.path.append("..")
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
    if not is_training:
        #如果是预测模式下，直接使用传入的移动平均所的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2,4)
        if len(X.shape ):
            #使用全连接层的情况下，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
            # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

自定义一个BatchNorm层

class BatchNorm(nn.Module):
    def __init__(self, num_features, num_dims):
        super(BatchNorm, self).__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化为0和1
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta == nn.Parameter(torch.zeros(shape))
        # 不参与求梯度和迭代的参数，全部初始化为0
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.zeros(shape)
        
    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to (X.device)
            self.moving_var = self.moving_var.to (X.device)
            
        # 保存更新后的参数，training属性默认为true， 调用.eval()后，设为false
        Y, self.moving_mean, self.moving_var = batch_norm(self.training, X, self.gamma, self.beta, self.moving_var, self.moving_mean, eps=1e-5, momentum=0.9)
        return Y

6.1.3 使用批量归一化层的LeNet

net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4),
                    nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
                    nn.Conv2d(6, 16,
                              kernel_size=5), BatchNorm(16, num_dims=4),
                    nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
                    nn.Flatten(), nn.Linear(16 * 4 * 4, 120),
                    BatchNorm(120, num_dims=2), nn.Sigmoid(),
                    nn.Linear(120, 84), BatchNorm(84, num_dims=2),
                    nn.Sigmoid(), nn.Linear(84, 10))

6.1.4 简洁实现

pytorch的nn模块定义的BatchNorm1d和BatchNorm2d类使用起来更加简单，两者分别用于全连接层和卷积层，都需要指定输入的num_features参数值

net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6),
                    nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
                    nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16),
                    nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
                    nn.Flatten(), nn.Linear(256, 120), nn.BatchNorm1d(120),
                    nn.Sigmoid(), nn.Linear(120, 84), nn.BatchNorm1d(84),
                    nn.Sigmoid(), nn.Linear(84, 10))

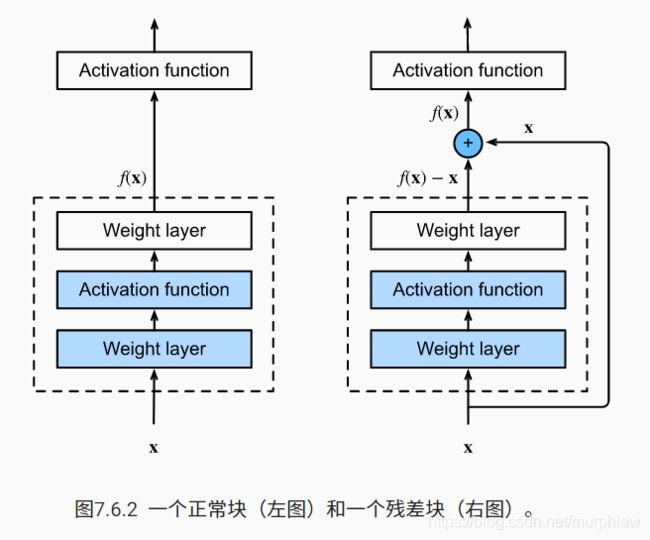
6.2 残差网络ResNet

6.3 稠密连结网络

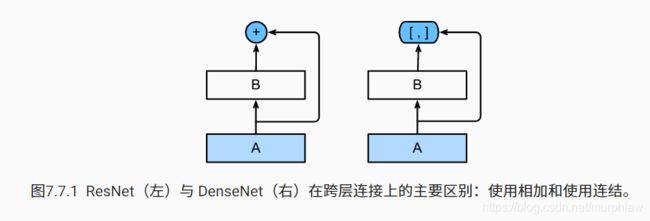
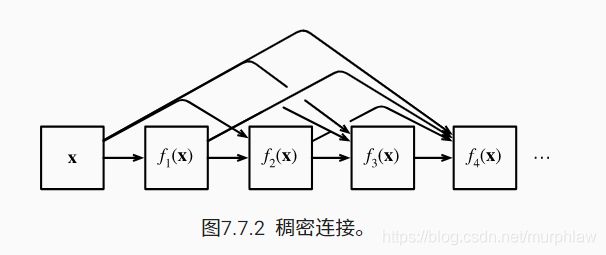
ResNet 和 DenseNet 的关键区别在于，DenseNet 输出是连接（用图中的 [,] 表示）而不是如 ResNet 的简单相加。 因此，在应用越来越复杂的函数序列后，我们执行从 x 到其展开式的映射：

(7.7.3)
x→[x,f1(x),f2([x,f1(x)]),f3([x,f1(x),f2([x,f1(x)])]),…].

最后，将这些展开式结合到多层感知机中，再次减少特征的数量。 实现起来非常简单：我们不需要添加术语，而是将它们连接起来。 DenseNet 这个名字由变量之间的“稠密连接”而得来，最后一层与之前的所有层紧密相连。