浙大版《C语言程序设计》第四版(何钦铭颜晖) 第10章 函数与程序结构 课后习题答案

你也可以上程序咖(https://meta.chengxuka.com)，打开大学幕题板块，不但有答案，讲解，还可以在线答题。

一、选择题

1.对于以下递归函数，调用f(4)，其返回值为（ ）。

int f(int n)
{
    if (n)
        return f(n - 1) + n;
    else
        return n;
}

A.10

B.4

C.0

D.以上均不是

答：A

解析：

递归函数的调用。

第一次调用函数 f，参数为 4，执行 if 语句，返回 f(3)+4，

第二次调用函数 f，参数为 3，执行 if 语句，返回 f(2)+3，

第三次调用函数 f，参数为 2，执行 if 语句，返回 f(1)+2，

第四次调用函数 f，参数为 1，执行 if 语句，返回 f(0)+1，

第五次调用函数 f，参数为 0，执行 else 语句，返回 0。

然后再一层一层将return 的结果返回。最终得到的就是 0 +1+2+3+4 = 10。

2.执行下列程序段后，变量 i 的值为（ ）。

#define MA(x, y) (x*y)
i=5;
i=MA(i, i+1)-7;

A.30

B.23

C.19

D.1

答：C

解析：

函数调用时，如果实参是表达式，要先计算表达式，再把结果值传递过去。而这里使用了宏定义。宏替换不作计算，直接替换进去。

MA(i, i+1)，按照 i * (i+1) 计算，i 带入给 x，i+1 带入给 y，那么 x * y 就是 x * x + 1 ，计算结果就是 26，再减掉 7，最终结果就是 19。

3.宏定义 "#define DIV(a, b) a/b"， 经 DIV(x+5, y-5) 引用，替换展开后是（ ）。

A. (x+5/y-5)

B. x+5/y-5

C. (x+5)/(y-5)

D. (x+5)/(y-5)

答：A

解析：

宏定义在使用的时候，宏替换不作计算，直接替换进去。 就是 (x+5/y-5)，选项 A 正确。

4.以下程序的输出结果是（ ）。

int x = 5, y = 7;
void swap()
{
    int z;
    z = x;
    x = y;
    y = z;
}
int main()
{
  int x = 3, y = 8;
    swap();
    printf("%d#%d\n", x, y);
    return 0;
}

A.8#3

B.3#8

C.5#7

D.7#5

答：B

解析：

题目中定义了全局变量 x=5，y=7，main() 中又定义了同名的局部变量 x=3，y=8。函数 swap ()，函数里交换了x 和 y 的值，操作的是全局变量。main() 中调用完函数后打印 x 和 y 的值，这里打印的是 main () 的局部变量，还是 3 和 8。所以选项 B 正确。

5.下面说法中正确的是（ ）。

A.若全局变量仅在单个 C 文件中访问，则可以将这个变量修改为静态全局变量，以降低模块间的耦合度

B.若全局变量仅由单个函数访问，则可以将这个变量改为该函数的静态局部变量，以降低模块间的耦合度

C.设计和使用访问动态全局变量、静态全局变量、静态局部变量的函数时，需要考虑变量生命周期问题

D.静态全局变量使用过多，将导致动态存储区(堆栈)溢出

答：A

解析：

A选项：变量分为全局变量和局部变量。局部变量和形参的作用域是函数内部，全局变量的作用域是整个文件。但可以通过声明一个extern的全局变量拓展全局变量的作用域，也可以通过定义一个static的全局变量限制这种拓展。

B选项：如果全局变量仅仅由单个函数访问，不存在耦合度的问题

C选项：动态全局变量、静态全局变量、静态局部变量的生命周期都为程序运行期间，其中静态局部变量的生存周期虽然为整个源程序，但是其作用域仍然与局部变量相同，当退出函数是，该变量还存在，但是不能使用。

D选项：全局变量和静态变量都是存储在静态存储区，所以在递归调用是不会压栈，也不会造成堆栈溢出。

6.以下 main() 函数中所有可用的变量为（ ）。

void fun(int x)
{
  static int y;
  .....
}
int z;
int main()
{
  int a, b;
  fun(a);
  .....
}

A.x,y

B.x,y,z

C.a,b,x,y, z

D.a,b,z

答：D

解析：

在 main() 中可以使用的变量包括 main() 中声明的局部变量 a 和 b，以及全局变量 z

二、填空题

1.对于以下递归函数，调用f(3)，其返回值为（ ）。

int f(int x)
{
  return((x>0)? f(x-1)+f(x-2): 1); 
}

答：5

解析：

这里是递归函数调用：

f(3)
    = f(2)+f(1)
    = f(1)+ f(0) + f(1) = f(1)+1+f(1)
    = f(0)+ f(-1) + 1 + f(0)+f(-1) = 1+1+1+1+1
    = 5
    

2.输入 6 ，下列程序的运行结果是（ ）。

#include 
int f(int n, int a)
{
    if (n == 0)
        return a;
    return f(n - 1, n * a);
}
int main(void)
{
    int n;
    scanf("%d", &n);
    printf("%d\n", f(n, 1));
    return 0;
}

答：720

解析：

这里 f 函数时递归调用，当 n 为 6 时，第一次调用函数，传入参数 n 为 6，a 为 1。

f(6,1)
        = f(5,6)
        = f(4,30)
        = f(3,120)
        = f(2, 360)
        = f(1,720)
        = f(0, 720)
        = 720

3.下列程序的输出结果为（ ）。

#include 
int f(int g)
{
    switch (g)
    {
    case 0:
        return 0;
    case 1:

    case 2:
        return 2;
    }
    printf("g=%d\n", g);
    return f(g - 1) + f(g - 2);
}
int main(void)
{
    int k;
    k = f(4);
    printf("k=%d\n", k);
    return 0;
}

答：

g=4

g=3

k=6

解析：

递归函数调用：

k = f(4)
     打印 g=4
     = f(3)+f(2)    = f(3)+2
  打印 g=3
  = f(2)+f(1) = 2+2+2 = 6
  打印 k = 6

4.C 语言的编译预处理功能主要包括和（ ）、（ ）和（ ）。

答：宏定义、文件包含、条件编译

解析：

编译预处理时 C 语言编译程序的组成部分，它用于解释处理 C 语言源程序中的各种预处理指令。

预处理功能是由很多预处理命令组成，这些命令在编译时进行通常的编译功能(包含词法和语言分析、代码生成、优化等)之前进行处理。预处理后的结果和源程序一起在进行通常的编译操作，进而得到目标代码。预处理功能主要包括：宏定义、文件包含、条件编译。

5.下列语句的运算结果为（ ）。

#define F(x) x-2
#define D(x) x*F(x)
printf("%d,%d", D(3), D(D(3)));

答：7,-13

解析：

宏定义，是直接将数值带入。

 D(3),
=3*F(3)
=3*3-2
=7


 D(D(3)) 
=D(3)*F(D(3))
=3*F(3)*D(3)-2
=3*3-2*3*F(3)-2
=3*3-2*3*3-2-2
=9-18-2-2
=-13

三、程序设计题

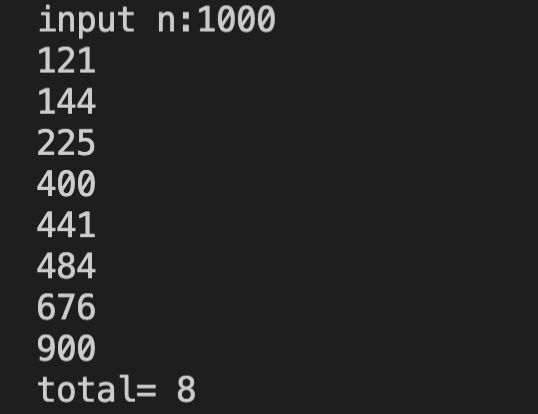
题目1：判断满足条件的三位数：编写一个函数，利用参数传入一个 3 位数 n ，找出 101～ n 间所有满足下列两个条件的数：它是完全平方数，又有两位数字相同，如 144、676 等，函数返回找出这样的数据的个数。试编写相应程序。

答案代码：

#include 
#include 
int fun(int n);
int main()
{
    // 习题(10.3.1)
    /*
    判断满足条件的三位数：编写一个函数，利用参数传入一个 3 位数 n ，
    找出 101～ n 间所有满足下列两个条件的数：它是完全平方数，又有两位数字相同，如 144、676 等，函数返回找出这样的数据的个数。

    */

    int n;
    printf("input n:");
    scanf("%d", &n);
    printf("total= %d\n", fun(n));
    return 0;
}
int fun(int n)
{
    int i, d = 0;
    for (i = 101; i <= n; i++)
        if (((int)sqrt(i) * (int)sqrt(i)) == i)
        {
            if (i / 100 == (i / 10) % 10 || i / 100 == i % 10 || (i / 10) % 10 == i % 10)
            {
                printf("%d\n", i);
                d++;
            }
        }
    return d;
}

运行结果：

题目2：递归求阶乘和：输入一个整数 n（ n>0 且 n≤10），求 1!+2!+3!+...+n!。 定义并调用函数 fact(n) 计算 n!，函数类型是 double。试编写相应程序。

答案代码：

#include 
double fact(int n);
int main()
{
    // 习题(10.3.2)
    /*
    递归求阶乘和：输入一个整数 n（ n>0 且 n≤10），求 1!+2!+3!+...+n!。
    定义并调用函数 fact(n) 计算 n!，函数类型是 double。
    */

    int i, n;
    double sum = 0;
    printf("input n:");
    scanf("%d", &n);
    for (i = 1; i <= n; i++)
        sum = sum + fact(i);
    printf("%.0lf\n", sum);
    return 0;
}

double fact(int n)
{
    int result = 0;
    if (n == 1)
        result = 1;
    if (n > 1)
        result = n * fact(n - 1);
    return result;
}

运行结果：

题目3：递归实现计算 xⁿ ：输入实数 x 和正整数 n，用递归函数计算 xⁿ 的值。试编写相应程序。

答案代码：

#include 
int rec(int x, int n);
int main()
{
    // 习题(10.3.3)
    /*
    递归实现计算 x^n ：输入实数 x 和正整数 n，用递归函数计算 x^n 的值。
    */

    int x, n;
    printf("input x and n:");
    scanf("%d%d", &x, &n);
    printf("result : %d\n", rec(x, n));
    return 0;
}

int rec(int x, int n)
{
    if (n == 0)
        return 1;
    else
        return rec(x, n - 1) * x;
}

运行结果：

题目4：递归求式子和：输入实数 x 和正整数 n，用递归的方法对下列计算式子编写一个函数。

$$ f(x,n)=x-x^2+x^3-x^4+...+(-1)^{n-1}x^n(n>0) $$

试编写相应程序。

答案代码：

#include 

double f(double x, int n);
double js1(double z, int b);

int main()
{
    // 习题(10.3.4)
    /*
    递归求式子和：输入实数 x 和正整数 n，用递归的方法对下列计算式子编写一个函数。

    */

    double x;
    int n;
    printf("input x and n:");
    scanf("%lf%d", &x, &n);
    printf("%.2lf\n", f(x, n));
    return 0;
}

double f(double x, int n)
{
    double sum;
    double b;
    if (n == 0)
        return 0;
    int z;
    if (n % 2 == 0)
        z = -1;
    else
        z = 1;
    b = z * js1(x, n);
    sum = b + f(x, n - 1);

    return sum;
}

double js1(double x, int n)
{
    if (n == 0)
        return 1;
    return x * js1(x, n - 1);
}

运行结果：

题目5：递归计算函数 ack(m, n) ：输入 m 和 n ，编写递归函数计算 Ackermenn 函数的值：

$$ ack(m,n)= \begin{cases} n+1 & m=0\\ ack(m-1,1) & n=0\&\&m>0\\ ack(m-1,ack(m,n-1)) & m>0 \&\& n>0 \end{cases} $$

试编写相应程序。

答案代码：

#include 
int Ack(int m, int n);

int main()
{
    // 习题(10.3.5)
    /*
    递归计算函数 ack(m, n) ：输入 m 和 n ，编写递归函数计算 Ackermenn 函数的值：
    */

    int m, n;
    int result;
    printf("input m and n:");
    scanf("%d%d", &m, &n);
    result = Ack(m, n);
    printf("Ackerman(%d,%d)=%d\n", m, n, result);
    return 0;
}
int Ack(int m, int n)
{
    if (m == 0)
        return n + 1;
    else if (n == 0)
        return Ack(m - 1, 1);
    else
        return Ack(m - 1, Ack(m, n - 1));
}

运行结果：

题目6：递归实现求 Fabonacei 数列：用递归方法编写求斐波那契数列的函数，函数类型为整型，斐波那契数列的定义如下。试编写相应程序。

$$ f(n)=f(n-2)+f(n-1)(n>1) $$

其中 f(0)=0，f(1)= 1。

答案代码：

#include 

long fib(int n);
int main()
{
    // 习题(10.3.6)
    /*
    递归实现求 Fabonacei 数列：用递归方法编写求斐波那契数列的函数，函数类型为整型，斐波那契数列的定义如下。
    */

    int n;
    printf("input n:");
    scanf("%d", &n);
    printf("fib(%d)=%ld\n", n, fib(n));
    return 0;
}

long fib(int n)
{
    long res;
    if (n == 0)
        res = 0;
    else if (n == 1)
        res = 1;
    else
        res = fib(n - 2) + fib(n - 1);
    return res;
}

运行结果：

题目7：递归实现十进制转换二进制：输入一个正整 n，将其转换为二进制后输出。要求定义并调用函数 dectobin(n)，它的功能是输出 n 的二进制。试编写相应程序。

答案代码：

#include 

void dectobin(int n);
int main()
{
    // 习题(10.3.7)
    /*
    递归实现十进制转换二进制：输入一个正整 n，将其转换为二进制后输出。
    要求定义并调用函数 dectobin(n)，它的功能是输出 n 的二进制。
    */

    int n;
    printf("input n:");
    scanf("%d", &n);
    dectobin(n);
    printf("\n");
    return 0;
}

void dectobin(int n)
{
    if (n == 0)
        return;
    else
    {
        dectobin(n / 2);
        printf("%d", n % 2);
    }
}

运行结果：

题目8：递归实现顺序输出整数：输入一个正整数 n，编写递归函数实现对其进行按位顺序输出。试编写相应程序。

答案代码：

#include 

void printdigits(int n);
int main()
{
    // 习题(10.3.8)
    /*
    递归实现顺序输出整数：输入一个正整数 n，编写递归函数实现对其进行按位顺序输出。
    */

    int n;
    printf("input n:");
    scanf("%d", &n);
    printdigits(n);
    return 0;
}

void printdigits(int n)
{
    if (n < 10)
        printf("%d\n", n);
    else
    {
        printdigits(n / 10);
        printf("%d\n", n % 10);
    }
}

运行结果：

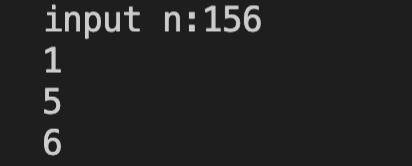
题目9：输入 n（n<10）个整数，统计其中素数的个数。要求程序由两个文件组成，一个文件中编写 main 函数，另一个文件中编写素数判断的函数。使用文件包含的方式实现。试编写相应程序。

答案代码：

#include 
#include 
#include "Prime.c"

int main()
{
    // 习题(10.3.9)
    /*
    输入 n（n<10）个整数，统计其中素数的个数。要求程序由两个文件组成，
    一个文件中编写 main 函数，另一个文件中编写素数判断的函数。使用文件包含的方式实现。
    */
    int n;
    int count = 0;
    printf("input numbers:");
    while (1)
    {
        scanf("%d", &n);
        if (prime(n))
        {
            count++;
        }
        if (getchar() == '\n')
        {
            break;
        }
    }

    printf("其中素数的个数为:%d\n", count);
    return 0;
}

prime.c 文件：

int prime(int n)
{
    int flag = 1; // 1:是素数  0:不是素数
    int count = 0;

    if (n == 1)
    {
        flag = 0;
    }
    else
    {
        count = 0;
        for (int j = 2; j <= sqrt(n); j++)
        {
            if (n % j == 0)
            {
                count++;
                break;
            }
        }
        if (!count)
        {
            return 1;
        }
    }

    return 0;
}

运行结果：

题目10：三角形面积为：

$$ area=\sqrt{s\times(s-a)\times(s-b)\times(s-c)} \\ s=(a+b+c) / 2 $$

其中 a、b、c 分别是三角形的 3 条边。请分别定义计算 s 和 area 的宏，再使用函数实现。比较两者在形式上和使用上的区别。

答案代码：

(1) 使用宏实现

#include 
#include 

#define S(a, b, c) ((a) + (b) + (c)) / 2
#define AREA(s, a, b, c) sqrt((s) * ((s) - (a)) * ((s) - (b)) * ((s) - (c)))

int main()
{
    // 习题(10.3.10)
    /*
    三角形面积为：
    $$
    area=\sqrt{s\times(s-a)\times(s-b)\times(s-c)} \\
    s=(a+b+c) / 2
    $$

    其中 a、b、c 分别是三角形的 3 条边。请分别定义计算 s 和 area 的宏，再使用函数实现。比较两者在形式上和使用上的区别。


    */

    double a, b, c, s;
    printf("input a,b,c:");
    scanf("%lf%lf%lf", &a, &b, &c);
    s = S(a, b, c);
    printf("area = %lf\n", AREA(s, a, b, c));

    return 0;
}

运行结果：

(2) 使用函数实现

#include 
#include 

double p(double a, double b, double c);

double area(double a, double b, double c);

int main()
{
    // 习题(10.3.10)
    /*
    三角形面积为：
    $$
    area=\sqrt{s\times(s-a)\times(s-b)\times(s-c)} \\
    s=(a+b+c) / 2
    $$

    其中 a、b、c 分别是三角形的 3 条边。请分别定义计算 s 和 area 的宏，再使用函数实现。比较两者在形式上和使用上的区别。


    */

    double a, b, c, s;
    printf("input a,b,c:");
    scanf("%lf%lf%lf", &a, &b, &c);
    printf("area = %lf\n", area(a, b, c));

    return 0;
}

double p(double a, double b, double c)
{
    return (a + b + c) / 2;
}
double area(double a, double b, double c)
{
    double s = p(a, b, c);
    return sqrt(s * (s - a) * (s - b) * (s - c));
}

运行结果：

题目11：有序表的增删改查操作。首先输入一个无重复元素的、从小到大排列的有序表，并在屏幕上显示以下菜单，用户可以反复对该有序表进行插入、删除、修改和查找操作，也可以选择结束。当用户输入编号 1~4 和相关参数时，将分别对该有序表进行插入、删除、修改和查找操作，输入其他编号，则结束操作。
[1 ] Insert
[2] Delete
[3] Modify
[4] Query
[other option] End

答案代码：

/* 有序表的增删改查操作 */
#include 
#define MAXN 10000 /* 定义符号常量表示数组a的长度 */

int Count = 0;                                 /* 用全局变量Count表示数组a中待处理的元素个数 */
void select(int a[], int option, int value); /* 决定对有序数组a进行何种操作的控制函数 */
int input_array(int a[]);                     /* 输入有序数组a的函数 */
void print_array(int a[]);                     /* 输出有序数组a的函数 */
int insert(int a[], int value);                 /* 在有序数组a中插入一个值为value的元素的函数 */
int del(int a[], int value);                 /* 删除有序数组a中等于value的元素的函数 */
int modify(int a[], int value1, int value2); /* 将有序数组a中等于value1的元素，替换为value2 */
int query(int a[], int value);                 /* 用二分法在有序数组a中查找元素value的函数 */

int main()
{
    // 习题(10.3.1)
    /*
    有序表的增删改查操作。首先输入一个无重复元素的、从小到大排列的有序表，并在屏幕上显示以下菜单，用户可以反复对该有序表进行插入、删除、修改和查找操作，也可以选择结束。当用户输入编号 1~4 和相关参数时，将分别对该有序表进行插入、删除、修改和查找操作，输入其他编号，则结束操作。
    [1 ] Insert
    [2] Delete
    [3] Modify
    [4] Query
    [other option] End
    */

    int option, value, a[MAXN];

    if (input_array(a) == -1)
    {                     /* 调用函数输入有序数组 a */
        printf("Error"); /* a不是有序数组，则输出相应的信息 */
        return 0;
    }

    printf("[1] Insert\n"); /* 以下4行显示菜单*/
    printf("[2] Delete\n");
    printf("[3] Update\n");
    printf("[4] Query\n");
    printf("[Other option] End\n");
    while (1)
    { /* 循环 */
        printf("input you select:");
        scanf("%d", &option); /* 接受用户输入的编号 */
        if (option < 1 || option > 4)
        { /* 如果输入1、2、3、4以外的编号，结束循环 */
            break;
        }
        printf("input value:");
        scanf("%d", &value);      /* 接受用户输入的参数value */
        select(a, option, value); /* 调用控制函数 */
        printf("\n");
    }
    printf("Thanks.\n"); /* 结束操作 */

    return 0;
}

/* 控制函数 */
void select(int a[], int option, int value)
{
    int index, value2;

    switch (option)
    {
    case 1:
        index = insert(a, value); /* 调用插入函数在有序数组 a 中插入元素value */
        if (index == -1)
        { /* 插入数据已存在，则输出相应的信息 */
            printf("Error");
        }
        else
        {
            print_array(a); /* 调用输出函数，输出插入后的有序数组a */
        }
        break;
    case 2:
        index = del(a, value); /* 调用删除函数在有序数组 a 中删除元素value */
        if (index == -1)
        { /* 没找到value，则输出相应的信息 */
            printf("Deletion failed.");
        }
        else
        {
            print_array(a); /* 调用输出函数，输出删除后的有序数组a */
        }
        break;
    case 3:
        printf("input value2:");
        scanf("%d", &value2);              /* 接受用户输入的参数value2 */
        index = modify(a, value, value2); /* 调用修改函数在有序数组 a 中修改元素value的值为value2 */
        if (index == -1)
        { /* 没找到value或者vaule2已存在，则输出相应的信息 */
            printf("Update failed.");
        }
        else
        {
            print_array(a); /* 调用输出函数，输出修改后的有序数组a */
        }
        break;
    case 4:
        index = query(a, value); /* 调用查询函数在有序数组 a 中查找元素value */
        if (index == -1)
        { /* 没找到value，则输出相应的信息 */
            printf("Not found.");
        }
        else
        { /* 找到，则输出对应的下标 */
            printf("%d", index);
        }
        break;
    }
}

/* 有序表输入函数 */
int input_array(int a[])
{
    printf("input n:");
    scanf("%d", &Count);
    for (int i = 0; i < Count; i++)
    {
        scanf("%d", &a[i]);
        if (i > 0 && a[i] <= a[i - 1])
        { /* a不是有序数组 */
            return -1;
        }
    }

    return 0;
}

/* 有序表输出函数 */
void print_array(int a[])
{
    for (int i = 0; i < Count; i++)
    { /* 输出时相邻数字间用一个空格分开，行末无空格 */
        if (i == 0)
        {
            printf("%d", a[i]);
        }
        else
        {
            printf(" %d", a[i]);
        }
    }
}

int insert(int a[], int value)
{
    int i, j, flag = 0;

    for (i = 0; i < Count; i++)
    {
        if (a[i] == value)
        {
            flag = 1;
            break;
        }
        else
        {
            if (value < a[i])
            {
                break;
            }
        }
    }
    if (flag == 1)
    {
        return -1;
    }
    else
    {
        for (j = Count - 1; j >= i; j--)
        {
            a[j + 1] = a[j];
        }
        a[i] = value;
        Count++;
    }

    return 0;
}

int del(int a[], int value)
{
    int i, j, flag = 0;

    for (i = 0; i < Count; i++)
    {
        if (a[i] == value)
        {
            flag = 1;
            break;
        }
    }
    if (flag == 0)
    {
        return -1;
    }
    else
    {
        for (j = i; j < Count - 1; j++)
        {
            a[j] = a[j + 1];
        }
        Count--;
    }

    return 0;
}

int modify(int a[], int value1, int value2)
{
    if (del(a, value1) == -1)
    {
        return -1;
    }
    if (insert(a, value2) == -1)
    {
        return -1;
    }

    return 0;
}

int query(int a[], int value)
{
    int left = 0, right = Count - 1, mid, flag = 0;

    while (left <= right)
    {
        mid = (left + right) / 2;
        if (value == a[mid])
        {
            flag = 1;
            return mid;
        }
        else if (value < a[mid])
        {
            right = mid - 1;
        }
        else
        {
            left = mid + 1;
        }
    }
    if (flag == 0)
    {
        return -1;
    }
}

运行结果：