不会深度优先搜索?看这篇文章就对了 算法详解之深度优先搜索
前言
大家好,我是泡泡,一名算法爱好者,在学习算法的这条路上有很多的坎坷与‘大山’,想必各位都深有体会,我认为学习算法的几个很卡的点,首当其冲就是深度优先搜索和广度优先搜索,虽然理解了是什么意思但是完全敲不出来代码,练基础的题也不会写,导致了自己很迷惑,之前学的排序一类的并没有这种情况,为什么呢?实际上是因为你没有在了解算法的同时记住这个模板,y总有句话讲的很好,你并不是在构造算法,你是在学习使用模板,是啊,这是人类历史上几十年甚至上百年各个科学家智慧的结晶,对于初学肯定很难,所以就有了今天这篇文章。
今天这篇文章,就是为了帮助还卡在深度优先搜索,实在不会写代码的同学们,看了这篇文章可能会给你不一样的体验,这里效仿了闫式dp分析法做了一个自己的简单的dfs四步法,牢记四步,迷宫问题,排列问题完全不怕不会做!
目录
算法简述
练习1:海战
题目描述
输入格式
输出格式
练习2:排列
题目描述
输入格式
输出格式
总结
算法简述
深度优先搜索:
它是图的遍历方法的一种,用栈来实现,深度优先搜索和树的先序遍历比较类似。
它的思想用人话来说就是不撞南墙不回头,一直走一个点直到不能走再考虑其他方向,直到所有的点都被遍历过。显然,深度优先搜索是一个递归的过程。
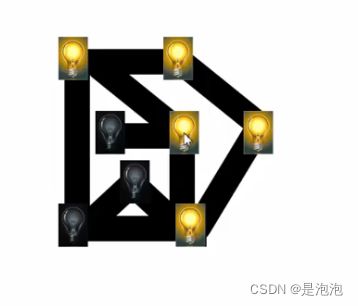
可能光说不能感受到他的魅力,我们上图来了解一下。
因为博主画画太丑了,所以借用了浙大数据结构的图,这里是一个图,所有点都没访问过
然后我们从第一个点开始,灯泡点亮了,如果在代码里我们就需要一个数组来记录走过的路。
然后我们往右边走,发现没走过,然后走到这
到这里之后发现只能往左走,那就继续往走左
此时这里我们发现有两条路可以走,用犹豫嘛?不用,我们最终都遍历的,所以干就完了,选择上面,走!
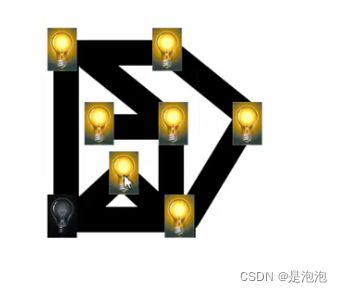
走完之后,我们发现无路可走了,于是我们原路返回,返回刚才做选择的位置。
然后选择没有走过的地方继续走
结束
相信大家看图可以很明白地看到深度优先搜索是怎么运作的,但是实际应用的情况代码应该如何去写呢,我这里先拿出来一个自己写的简易模版来给大家看一下理解一下,然后我们引入几个例子让大家更深入地去理解深度优先搜索。
按照我们四步法来,第一步,存图,方向,标记数组
大家要读题来决定,存图数组,方向数组,标记数组开成什么样子,这里以正常二维数组和上下左右来写
const int N = 10001;
int dx[] = {0,1,-1,0};
int dy[] = {1,0,0,-1};
int s[N][N];
bool vis[N][N];第一层是数据范围,第二层第三层是方向,如果你 此时在1 1 那么+0 +1就变成1 2 那么就是右边一个,+1 +0就是2 1变往下走一个。四个方向都这么来就好,如果是八个方向需要多一些
int dx[] = {1,0,0,-1,1,-1,1,-1}
int dy[] = {0,1,-1,0,1,-1,-1,1}第一步解决了,我们开始第二步
第二步:找到起始点,题目要求,开始dfs
比如要求我们找连通块,我们可以循环整个图,两个for进去,然后如果图的位置等于哪个连通块的字符或者数字,就进入搜索,代码如下
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(s[i][j]=='*')
{
dfs(i,j);
}
}
}然后就是我们的第三步,dfs函数的写法
dfs函数怎么写,首先标记当前位置已经走过,然后写一个循环,有几个方向循环几层,循环里写判断是否越界走过,是否满足要求,没有就继续递归下去,代码如下
bool pd(int x,int y)
{
if(x<1||x>n||y<1||y>m)
{
return false;
}
if(vis[x][y])
{
return false;
}
return true;
}
void dfs(int x, int y)
{
vis[x][y] = 1;
for(int i=0;i<4;i++)
{
int xx = x+dx[i];
int yy = y+dy[i];
if(pd(xx,yy)&&s[xx][yy]=='.')
{
dfs(x+xx[i],y+yy[i]);
}
}
}第四步就是保存答案输出,这就很简单了,我们就不放代码了。
综上所述,我们就学会了一个联通块dfs的代码模板,遇到联通块问题我们就可以用这四步,妥妥的解决,大家先看一下记一下这四步,然后我们做两道题来巩固一下!
练习1:海战
题目描述
在峰会期间,武装部队得处于高度戒备。警察将监视每一条大街,军队将保卫建筑物,领空将布满了F-2003飞机。此外,巡洋船只和舰队将被派去保护海岸线。不幸的是因为种种原因,国防海军部仅有很少的几位军官能指挥大型海战。因此,他们考虑培养一些新的海军指挥官,他们选择了“海战”游戏来帮助学习。
在这个著名的游戏中,在一个方形的盘上放置了固定数量和形状的船只,每只船却不能碰到其它的船。在这个题中,我们仅考虑船是方形的,所有的船只都是由图形组成的方形。编写程序求出该棋盘上放置的船只的总数。
输入格式
输入文件头一行由用空格隔开的两个整数R和C组成,1<=R,C<=1000,这两个数分别表示游戏棋盘的行数和列数。接下来的R行每行包含C个字符,每个字符可以为“#”,也可为“.”,“#”表示船只的一部分,“.”表示水。
输出格式
为每一个段落输出一行解。如果船的位置放得正确(即棋盘上只存在相互之间不能接触的方形,如果两个“#”号上下相邻或左右相邻却分属两艘不同的船只,则称这两艘船相互接触了)。就输出一段话“There are S ships.”,S表示船只的数量。否则输出“Bad placement.”。
6 8 .....#.# ##.....# ##.....# .......# #......# #..#...#
以上就是一个最简单的判断连通块的问题,我们直接套用四步法,第一步,存图,方向,标记。
因为题目要求是四个方向,二位数组,所以我们按上面的开就好。
代码:
#include
using namespace std;
const int N = 1001;
int dx[] = {1,0,0,-1};
int dy[] = {0,1,-1,0};
char s[N][N];
bool vis[N][N];
int main()
{
int r,c;
cin>>r>>c;
for(int i=1;i<=r;i++)
{
for(int j=1;j<=c;j++)
{
cin>>s[i][j];
}
}
return 0;
} 然后是我们的第二步,找到起点,题目要求,开始dfs
题目要求 不能有相邻的船,题目这个意思就是一个2*2的格子里如果有三个船体就是相邻的,所以是错误的,要写一个函数来单独判断,起点就是遇到的任何一个没走过的船体。
bool pd(int a,int b)
{
int sum = 0;
if(s[a][b]=='#')
{
sum++;
}
if(s[a+1][b]=='#')
{
sum++;
}
if(s[a][b+1]=='#')
{
sum++;
}
if(s[a+1][b+1]=='#')
{
sum++;
}
if(sum==3)
{
return false;
}
return true;
}这是判断函数 下,右下右四个方向,判断是否有炸船。
然后就是我们的找起点代码
for(int i=1;i<=r;i++)
{
for(int j=1;j<=c;j++)
{
if(s[i][j]=='#'&&vis[i][j]==0)
{
dfs(i,j);
}
}
}
找到船体#就开搜。
然后就是我们的第三步,写dfs。
dfs怎么写呢,记得我们上面说的,越界,走没走过,循环。
bool yuejie(int x,int y)
{
if(x<1||x>r||y<1||y>c)
{
return false;
}
if(vis[x][y])
{
return false;
}
return true;
}
void dfs(int x,int y)
{
vis[x][y] = 1;
for(int i=0;i<4;i++)
{
int xx = x+dx[i];
int yy = y+dy[i];
if(yuejie(xx,yy)&&s[xx][yy]=='#')
{
dfs(xx,yy);
}
}
}第四步就是我们的答案,我们首先判断是否炸船,然后再定义一个变量,每次进入联通块就+1就好了,如果炸船直接输出结束,不用判断了就。
完整代码如下
#include
using namespace std;
const int N = 1001;
int dx[] = {1,0,0,-1};
int dy[] = {0,1,-1,0};
char s[N][N];
bool vis[N][N];
int r,c;
int num;
bool yuejie(int x,int y)
{
if(x<1||x>r||y<1||y>c)
{
return false;
}
if(vis[x][y])
{
return false;
}
return true;
}
void dfs(int x,int y)
{
vis[x][y] = 1;
for(int i=0;i<4;i++)
{
int xx = x+dx[i];
int yy = y+dy[i];
if(yuejie(xx,yy)&&s[xx][yy]=='#')
{
dfs(xx,yy);
}
}
}
bool pd(int a,int b)
{
int sum = 0;
if(s[a][b]=='#')
{
sum++;
}
if(s[a+1][b]=='#')
{
sum++;
}
if(s[a][b+1]=='#')
{
sum++;
}
if(s[a+1][b+1]=='#')
{
sum++;
}
if(sum==3)
{
return false;
}
return true;
}
int main()
{
cin>>r>>c;
for(int i=1;i<=r;i++)
{
for(int j=1;j<=c;j++)
{
cin>>s[i][j];
}
}
for(int i=1;i<=r;i++)
{
for(int j=1;j<=c;j++)
{
if(pd(i,j)==false)
{
cout<<"Bad placement.";
return 0;
}
}
}
for(int i=1;i<=r;i++)
{
for(int j=1;j<=c;j++)
{
if(s[i][j]=='#'&&vis[i][j]==0)
{
num++;
dfs(i,j);
}
}
}
printf("There are %d ships.",num);
return 0;
} 直接AC!其实这个代码可以不用vis,让代码量更小,大家可以思考自己写一下。
ps:修改原图数值
如果你跟下来的话你应该理解了联通块dfs如果解决了吧,我准备了几道题,大家一定要联系一下,记住我的四步法然后自己去解决,你解决一个dfs你自己就会了!
洛谷:P1451 求细胞数量 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P1596 [USACO10OCT]Lake Counting S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题都不难,大家自己敲一遍!
然后就是我们的全排列了。
全排列也是四步法,这里拿最经典的一个全排列问题来讲解
练习2:排列
题目描述
按照字典序输出自然数 1 到 n 所有不重复的排列,即 n 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
输入格式
一个整数 nn。
输出格式
由 1∼n 组成的所有不重复的数字序列,每行一个序列。
每个数字保留 5 个场宽。
看到这个题,很多人都笑了,这题也是很简单,这里四步法给大家讲一下
第一步,我们没有了方向数组,就是判断是否用过和存值数组。
int n,pd[100],a[100];第二步,找到起始点,题目要求,开始dfs
起始点自然是0,然后直接搜。
int main()
{
cin>>n;
dfs(0);
return 0;
}第三步,写dfs函数
题目要求是n,所以我们首先要判断有没有达到题目要求,达到就输出返回,不达到就接着往下搜,因为题目要求了n,所以循环以=n结束,每次判断该数有没有用过,没有用过我们就保存起来,然后写一个简单的记忆化搜索,因为用完之后返回,如果不清理现场那么就很乱了。
比如用123456了,如果你不归0,那么下一次循环判断你数组里还是123456,会导致一些数据错误问题。
void dfs(int k)
{
if(k==n)
{
for(int i=1;i<=n;i++)
{
printf("%5d",a[i]);
}
printf("\n");
return ;
}
for(int i=1;i<=n;i++)
{
if(!pd[i])
{
pd[i]=1;
a[k+1]=i;
dfs(k+1);
pd[i]=0;
}
}
}第四步,就是我们的 过啦!哈哈哈哈
完整代码如下
#include
using namespace std;
int n,pd[100],a[100];
void dfs(int k)
{
if(k==n)
{
for(int i=1;i<=n;i++)
{
printf("%5d",a[i]);
}
printf("\n");
return ;
}
for(int i=1;i<=n;i++)
{
if(!pd[i])
{
pd[i]=1;
a[k+1]=i;
dfs(k+1);
pd[i]=0;
}
}
}
int main()
{
cin>>n;
dfs(0);
return 0;
} 这里依然给出两个练习题,大家课后自己练一下,会一个就都会了!
洛谷:P1036 [NOIP2002 普及组] 选数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P1157 组合的输出 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
总结
今天我们学习了dfs的联通块判断和全排列判断,这些是常用的,其他变种的需要我们的灵活多变了,联通块的四步法:1.存图方向判断2.起点 dfs3.dfs函数怎么写4.答案输出 全排列则是:1.存答案 判断2.起点 dfs3.dfs函数怎么写4.答案输出。这两个方法其实是差不多的,就是全排列没有方向,多的是对这个数字是否使用的判断,大家牢记于心,方可攻破dfs!