Codeforces Round #789 (Div. 2)题解
Codeforces Round #789 (Div. 2)题解
A. Tokitsukaze and All Zero Sequence
原题链接
算法标签 贪心 排序
思路
情况一:数组存在零 → \rightarrow →非零数与其进行一次运算 → \rightarrow →答案即为非零个数
情况二:数组不存在零但存在相同数字 → \rightarrow →相同数字进行一次运算产生零 → \rightarrow →非零数与其进行一次运算 → \rightarrow →答案即为情况一+1
情况三:数组不存在零且不存在相同数字 → \rightarrow →不同数字进行一次运算产生相同数字 → \rightarrow →相同数字进行一次运算产生零 → \rightarrow →非零数与其进行一次运算 → \rightarrow →答案即为情况二+1
未初始化b数组,WA了一发
代码
#include
#define int long long
using namespace std;
const int N = 105;
int a[N],b[N];
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
int n;
cin>>n;
int cnt=0,ch=0;
memset(b,0, sizeof b);
for(int i=0;i>a[i];
if(!a[i]){
cnt++;
}
b[a[i]]++;
if(b[a[i]]==2){
ch=1;
}
}
sort(a,a+n);
if(cnt){
cout< B1. Tokitsukaze and Good 01-String (easy version
原题链接
算法标签 贪心 模拟
思路
进行字符串模拟,如果当前需处理字符串长度为奇数且该字符与上一个字符不一致,则更改该字符,使其与上一个字符一致。统计更改次数即为答案。
提交滴代码好冗余
代码
#include
#define int long long
using namespace std;
const int N = 105;
int a[N],b[N];
// 代码过于冗余
//string check(string s){
// int l=1;
// int left=1;
// int cnt=0;
// for(int i=left;i>t;
; while(t--){
string s;
int n;
cin>>n;
cin>>s;
//cout< B2. Tokitsukaze and Good 01-String (hard version)
原题链接
算法标签 贪心 模拟 字符串前缀 DP
思路
考虑从前向后的递推,可以发现对于前面已经维护好的前缀一定以"00"或"11"结尾,所以需要将每一个划分出来的
二元组转换成"00"或"11",通过枚举当前二元组变化成"00","11"的代价,在DP的过程中维护改变次数最少的情况
下,尽可能的使得当前串与前缀子段的结尾一致。
不会呀
代码
#include
using namespace std;
int main(){
int t;
cin>>t;
while(t--)
{
int n;
string s;
cin>>n>>s;
int ans=0, cnt=0;
int L=-1;
for(int i=0; i C. Tokitsukaze and Strange Inequality
原题链接
题意
给定一个长度为 n(n<=5000) 的数组p ,问有多少个4元组 (a, b, c, d) 满足 p[a]
算法标签 贪心 模拟
思路
枚举 b,c → \rightarrow →在 [1, b-1] 中小于p[c] 的个数,和在 [c+1, n] 中小于 p[b] 的个数 → \rightarrow →区间小于等于k的个数,离线加树状数组(复杂度为O(n^2logn)) → \rightarrow →预处理出pre[i][j]为区间 [1, i] 中小于等于j的个数。
哎 B2都不会
代码
void slove() {
cin >> n;
for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)pre[i][j] = 0;
for (int i = 1; i <= n; i++)cin >> p[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)pre[i][j] += pre[i - 1][j];
for (int j = p[i]; j <= n; j++)pre[i][j]++;
}
int ans = 0;
for (int b = 1; b <= n; b++) {
for (int c = b + 1; c <= n; c++) {
ans += pre[b - 1][p[c] - 1] * (pre[n][p[b]] - pre[c][p[b]]);
}
}
cout << ans << endl;
}
D. Tokitsukaze and Meeting
原题链接
题意
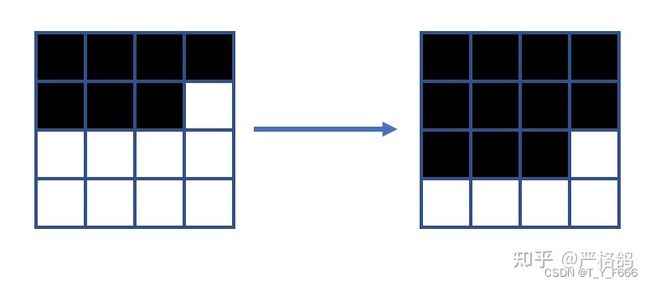
这里有一个 n*m 的格子,有 [公式] 的同学会从左上角进入,按照下面的方式。
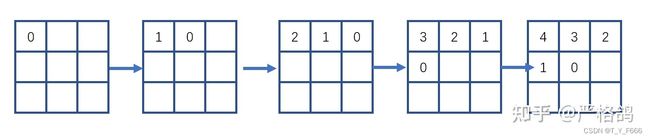
每个同学都有个属性, 0/1 ,每次进入一个学生后,问有多少行和多少列至少包含一个为 1 的学生。
样例
2 2
1100
输出
2 3 4 3
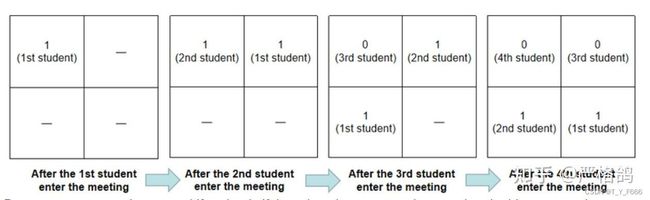
算法标签 思维 枚举
思路
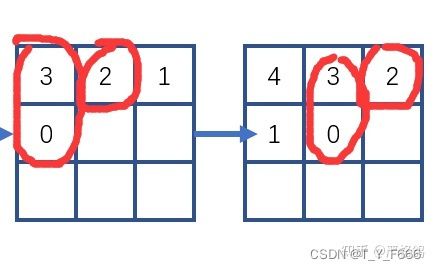
行列分开讨论 → \rightarrow →对于行, row[i] 为第 i 个学生进来时的答案(为了取模方便,学生的下标从0开始,下同row[i] 的答案可以由 row[i-m] 的答案变过来。 → \rightarrow →若最近 m 个学生里面有一个是1,答案加1 → \rightarrow →对于列,当插入一个学生后,等效为, 1, n-1 列向右移动。第 n 列提到前面。 → \rightarrow → col[m] 来记录提到前面来的情况,如果新插入的学生是1且提到前面来的列里面没有1,答案加1。 → \rightarrow →累加求和即为答案
哎 B2都不会
代码
void slove() {
cin >> n >> m;
vectorcol(m, 0); vectorrow(n*m, 0); vectorans(n*m, 0);
cin >> s;
int t = 0;
for (int i = 0; i < n*m; i++) {
if (s[i] == '1') {
if (col[i%m] == 0) {
col[i%m] = 1;
t++;
}
}
ans[i] += t;
}
int last = -1;
for (int i = 0; i < n*m; i++) {
if (s[i] == '1')last = i;
if (i < m) {
if (last != -1)row[i] = 1;
}
else {
if (i - last < m)row[i] = row[i - m] + 1;
else row[i] = row[i - m];
}
ans[i] += row[i];
}
for (int i = 0; i < n*m; i++)cout << ans[i] << " ";
cout << endl;
}
E. Tokitsukaze and Two Colorful Tapes
原题链接
题意
给定两个排列 a[], b[] ,你可以构造任意一个排列 p[] ,使得 a[i] = p[a[i]] , b[i] = p[b[i]]。使得 ∑ \sum ∑ |a[i] - b[i]|最大。输出最大值。
算法标签 图论 DFS 贪心 数学
思路
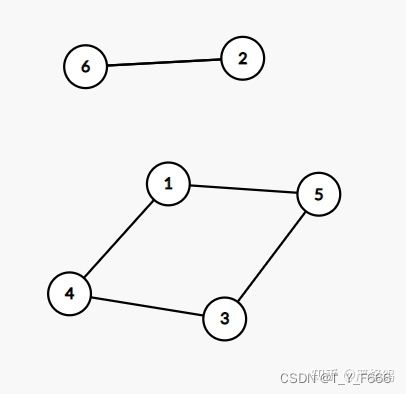
以样例为例
从图的角度, 理解 ∑ \sum ∑ |a[i] - b[i]| 。 → \rightarrow →建图 a[i] ↔ \leftrightarrow ↔b[i], → \rightarrow →答案即为环上相邻两个数差的绝对值之和
哎 B2都不会
注意
如果有环,我们一定可以构造一个 p[] ,使得环变为任意样子。
可理解为 p[] = named[] ,把环上的数进行重命名
只需为所有的环赋值即可。
如果环的长度为1,不会产生任何贡献。
若为偶数环,我们可以按照最大值,最小值交替来给环赋值(贪心,确保差值最大)。
for (int i = 0; i < c.size(); i++) {
if (i % 2 == 0)v.push_back(mx--);
else v.push_back(mi++);
}
若为奇数环,最后一个点无论如何赋值,不会改变其贡献。故奇数环的最后一个值无需放置,保留最大值和最小值。
因此,环的贡献函数:
int cal() {
if (c.size() == 1)return 0;
vectorv;
for (int i = 0; i < c.size() - c.size() % 2; i++) {
if (i % 2 == 0)v.push_back(mx--);
else v.push_back(mi++);
}
int res = 0;
for (int i = 1; i < v.size(); i++)res += abs(v[i] - v[i - 1]);
res += abs(v.back() - v[0]);
return res;
}
遍历所有环,累加即为答案。
代码
int n, a[MAXN], b[MAXN], to[MAXN];
bool vis[MAXN];
vectorc;
int mi, mx;
void dfs(int u) {
if (vis[u])return;
vis[u] = 1;
c.push_back(u);
dfs(to[u]);
}
int cal() {
if (c.size() == 1)return 0;
vectorv;
for (int i = 0; i < c.size() - c.size() % 2; i++) {
if (i % 2 == 0)v.push_back(mx--);
else v.push_back(mi++);
}
int res = 0;
for (int i = 1; i < v.size(); i++)res += abs(v[i] - v[i - 1]);
res += abs(v.back() - v[0]);
return res;
}
void slove() {
cin >> n;
for (int i = 1; i <= n; i++)vis[i] = 0;
mi = 1, mx = n;
for (int i = 1; i <= n; i++)cin >> a[i];
for (int i = 1; i <= n; i++)cin >> b[i], to[a[i]] = b[i];
int ans = 0;
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
c.clear();
dfs(i);
ans += cal();
}
}
cout << ans << endl;
}
战绩
战果
C-E主要借鉴该知乎
原创不易 转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈
![]()