【数据结构】栈和队列详细分析（全）

1.前言

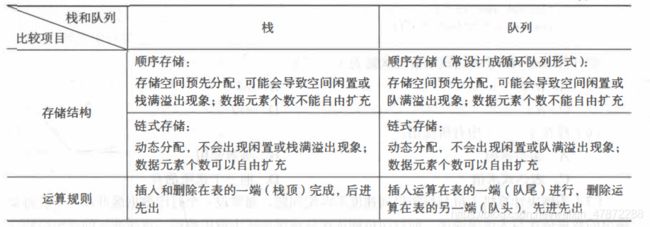
栈和队列是两种重要的线性结构。从数据结构角度看，栈和队列也是线性表， 其特殊性在于栈和队列的基本操作是线性表操作的子集，它们是操作受限的线性表，因此，可称为限定性的数据结构。

2.栈的定义与特点

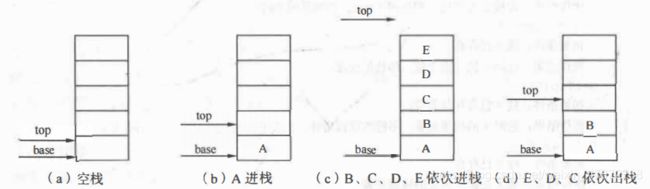
栈是限定仅在表尾进行插入或删除操作的线性表。 表尾称为栈顶,表头端称为栈底 。不含元素的空表称为空栈。栈的修改是按后进先出的原则进行的。

2.1顺序栈的定义

顺序栈是指利用顺序存储结构实现的栈，即利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，同时附设指针 top指示栈顶元素在顺序栈中的位置。通常习惯的做法是：以top=0表示空栈

顺序栈的存储结构：

#define MAXSIZE 100 //顺序栈存储空间的初始分配址
typedef struct{
SElemType *base;//栈底指针
SElemType *top;//栈顶指针
int stacksize;//栈可用的最大容扯
}SqStack; 

base 为栈底指针，初始化完成后，栈底指针 base 始终指向栈底的位置，若 base 的值为NULL, 则表明栈结构不存在。top 为栈顶指针，其初值指向栈底。每当插入新的栈顶元素时，指针 top 增1; 删除栈顶元素时，指针 top减1。因此，栈空时，top 和 base 的值相等，都指向栈底；栈非空时，top 始终指向栈顶元素的上一个

2.2顺序栈的操作

1.初始化

Status InitStack(SqStack &S) 
｛//构造一个空栈s
S.base=new SElemType[MAXSIZE]; //为顺序栈动态分配一个最大容扯为 MAXSIZE 的数组空间
if (!S.base) exit (OVERFLOW); //存储分配失败
S.top=S.base;//top 初始为 base, 空栈
S.stacksize=MAXSIZE; //stacksize 置为栈的最大容量 MAXSIZE
return OK;
}

2.入栈

先判定条件是否为满
先入栈后指针加1：*S.top++=e;

Status Push (SqStack &S, SElemType e) 
{//插入元素e为新的栈顶元素
if(S.top-S.base==S.stacksize) return ERROR; //栈满
*S.top++=e; //元素 e 压入栈顶， 栈顶指针加 1
return OK;
}

3.出栈

先判定条件是否为空
先指针减1后出栈：e=*–S.top;

Status Pop(SqStack &S,SElemType &e) 
（//删除s 的栈顶元素， 用 e 返回其值
if(S.top==S.base) return ERROR; 
e=*--S.top; 
return OK;
} 

4.取栈顶元素

SElemType GetTop{SqStack S) 
//返回 s 的栈顶元素， 不修改栈顶指针
if{S.top! =S.base) 
return *(S.top-1);
} 

2.3链栈的定义

链栈是指采用链式存储结构实现的栈
由于栈的主要操作是在栈顶插入和删除， 显然以链表的头部作为栈顶是最方便的， 而且没必要像单链表那样为了操作方便附加一个头结点。
链栈的存储结构：

typedef struct StackNode 
ElemType data;
struct StackNode *next; 
) StackNode,*LinkStack; 

2.4链栈的操作

1.初始化
构造一个空栈，没有设置头结点，只需要栈顶指针置空即可

Status InitStack(LinkStack &S) 
{//构造一个空栈 s, 栈顶指针置空
S=NULL; 
return OK;
}

2.入栈

分配空间生成新结点，将新结点设置为e，插入栈顶，在修改指针

Status Push(LinkStack &S, SElemType e) 
{//在栈顶插入元素e
p=new StackNode; //生成新结点
p->data=e;//将新结点数据域置为e
p->next=S;//将新结点插人栈顶
S=p; //修改栈顶指针为p
return OK; 
}

3.出栈

Status Pop(LinkStack &S,SElemType &e) 
{//删除 s 的栈顶元素，用 e 返回其值
if(S==NULL) return ERROR; //栈空
e=S->data; //将栈顶元素赋给 e
p=S; //用 p 临时保存栈顶元素空间， 以备释放
S=S->next; //修改栈顶指针
delete p; //释放原栈顶元素的空间
return OK;
}

4.取栈顶元素

SElemType GetTop(LinkStack S) 
{//返回 s 的栈顶元素， 不修改栈顶指针
if(S! =NULL) //栈非空
return S->data; //返回栈顶元素的值，栈顶指针不变
}

3.队列的定义与特点

和栈相反，队列是一种先进先出的线性表。它只允许在表的一端进行插入，而在另一端删除元素，允许插入的一端称为队尾，允许删除的一端则称为队头。

3.1循环队列

和顺序栈相类似，在队列的顺序存储结构中，除了用一组地址连续的存储单元，依次存放从队列头到队列尾的元素之外，尚需附设两个整型变最 front 和 rear分别指示队列头元素及队列尾元素的位置（后面分别称为头指针和尾指针）

队列的顺序存储结构：

#define MAXQSIZE 100//队列可能达到的最大长度 
typedef struct 
{
QElemType *base; //存储空间的基地址
int front; //头指针
int rear; //尾指针
}SqQueue; 

初始化创建空队列时，令 front = rear = 0 , 每当插入新的队列尾元素时，尾指针 rear增1; 每当删除队列头元素时， 头指针 front增1。因此，在非空队列中，头指针始终指向队列头元素，而尾指针始终指向队列尾元素的下一个位置

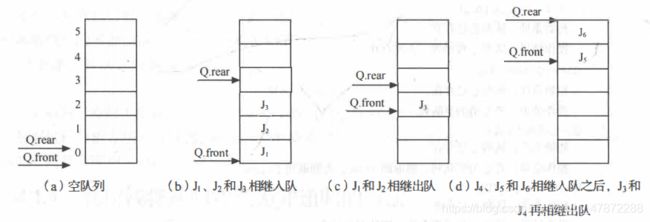
图中的d中这种现象为假溢出，数组越界，但还是有空间而导致程序非法，无法在填充数据，为了解决这种假溢出，推出了循环队列

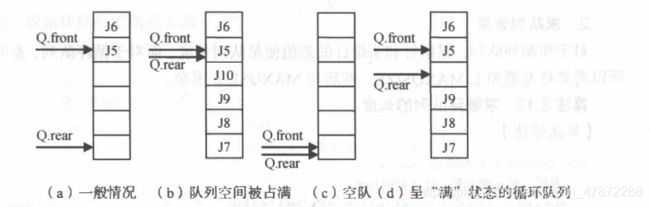
提示：在循环队列中如何区分队列是否满还是空？
方法一：少用一个元素空间， 即队列空间大小为m时，有m-1个元素就认为是队满。这样判断队空的条件不变， 即当头、 尾指针的值相同时， 则认为队空；而当尾指针在循环意义上加1后是等于头指针， 则认为队满。 因此， 在循环队列中队空和队满的条件是：
队空的条件： Q.front = Q.rear
队满的条件： (Q rear+ 1)%MAXSIZE = Q.front
方法二：另设一个标志位以区别队列是 “空” 还是 “满

3.2循环队列的操作

1.初始化

Status InitQueue (SqQueue &Q) 
{//构造一个空队列Q
Q.base=new QElemType[MAXQSIZE]；//为队列分配一个最大容扯为 MAXSIZE 的数组空间
if(!Q.base) exit(OVERFLOW);//存储分配失败
Q.front=Q.rear=0;//头指针和尾指针置为零， 队列为空
return OK;
}

2.求队列长度

int QueueLength(SqQueue Q) 
{//返回Q的元素个数， 即队列的长度
return(Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;
}

3.入队

判断条件是否为满，插入元素，队尾指针加1

Status EnQueue (SqQueue &Q, QElemType e) 
{//插入元素 e 为 Q 的新的队尾元素
if ((Q. rear+1) %MAXQSIZE==Q. front）//尾指针在循环意义上加1后等于头指针，表明队满
return ERROR; 
Q.base[Q.rear]=e;//新元素插入队尾
Q.rear=(Q.rear+1)%MAXQSIZE;//队尾指针加1
return OK; 
}

4.出队

判断条件是否为空，保存队头元素，对头指针加1

Status DeQueue (SqQueue &Q, QElemType &e) 
{//删除Q的队头元素， 用 e 返回其值
if(Q.front==Q. rear) return ERROR; / /队空
e=Q.base[Q.front]; //保存队头元素
Q.front=(Q.front+1)%MAXQSIZE; //队头指针加1
return OK;
}

5.取对头元素

SElemType GetHead(SqQueue Q) 
{//返回Q的队头元素，不修改队头指针
if(Q. front! =Q. rear) //队列非空
return Q.base[Q.front]; //返回队头元素的值，队头指针不变
}

3.3链队的定义

链队是指采用链式存储结构实现的队列。 通常链队用单链表来表
示。 一个链队显然需要两个分别指示队头和队尾的指针（分别称为头指针和尾指针）才能唯一确定。 这里和线性表的单链表一样， 为了操作方便起见，给链队添加一个头结点， 并令头指针始终指向头结点

链队的存储结构：

typedef struct QNode
{
QElemType data; 
struct QNode *next; 
}QNode, *QueuePtr; 

typedef struct 
QueuePtr front; //队头指针
QueuePtr rear; //队尾指针
) LinkQueue; 

链队的操作即为单链表插入和删除操作的特殊情况，只是需进一步修改尾指针或头指针。

3.4链队的操作

1.初始化

Status InitQueue (LinkQueue &Q) 
{//构造一个空队列 Q
Q.front=Q.rear=new QNode;//生成新结点作为头结点，队头和队尾指针指向此结点
Q.front->next=NULL;//头结点的指针域置空
return OK;
}

2.入队

Status EnQueue (LinkQueue &Q, QElemType e) 
{//插入元素e为Q的新的队尾元素
p=new QNode; //为人队元素分配结点空间，用指针p指向
p->data=e; //将新结点数据域置为e
p->next=NULL; Q. rear->next=p; //将新结点插入到队尾
Q.rear=p; //修改队尾指针
return OK;
}

3.出队

Status DeQueue(LinkQueue &Q,QElemType &e) 
{//删除Q的队头元素， 用e返回其值 
if(Q.front==Q.rear) return ERROR; //若队列空， 则返回 ERROR
p=Q.front->next; //p指向队头元素
e=p->data; //e保存队头元素的值 
Q.front->next=p->next; //修改头指针
if(Q.rear= =p) Q.rear=Q.front; //最后一个元素被删， 队尾指针指向头结点 
delete p; //释放原队头元素的空间
return OK; 
}

4.取队头元素

SElemType GetHead{LinkQueue Q) 
{//返回Q的队头元素， 不修改队头指针
if(Q.front!=Q.rear) //队列非空
return Q.front->next->data; //返回队头元素的值，队头指针不变
}

4.总结