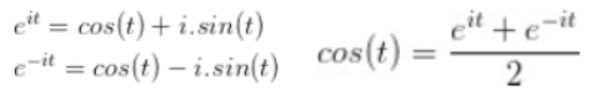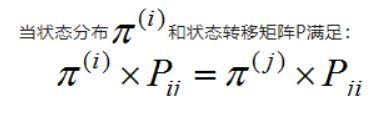机器学习/深度学习-学习笔记:概念补充(上)
学习时间:2022.05.09~2022.05.11
概念补充(上)
在进行学习机器学习和深度学习的过程中,对于部分概念会比较陌生(可能是因为没有系统深入学习过统计学、运筹学和概率统计的相关知识;也可能是因为看的东西比较偏实践,对理论的了解不是很深入),同时对有些概念的了解仅限于熟悉的或者用过的那几个,甚至有些概念会用但不知道具体的原理,所以想对其中的几个频繁出现的概念做个系统了解。主要包括:
- 上:极大似然估计、贝叶斯、傅里叶、马尔科夫、条件随机场;
- 下:凸集、凸函数与凸优化,优化算法(优化器),过拟合与欠拟合,正则化&归一化、标准化,损失函数和伪标签等。
文章目录
- 概念补充(上)
-
- 1. 极大似然估计 MLE
-
- 1.1 概念
- 1.2 公式
- 1.3 计算步骤
- 1.4 特点及应用
- 2. 贝叶斯 Bayes
-
- 2.1 贝叶斯定理/公式
- 2.2 贝叶斯估计的步骤
-
- 共轭先验 Conjugate Prior
- 2.3 朴素贝叶斯 Naive Bayes
- 2.4 贝叶斯优化 Bayesian Optimization
-
- 2.4.1 超参数调节方法
- 2.4.2 SMBO算法
- 2.4.4 Expected Improvement (EI)
- 2.4.3 不同概率分布的建模策略
- 2.4.4 Python应用
- 3. 傅里叶分析 Fourier
-
- 3.1 什么是频域
- 3.2 傅里叶变换是什么
- 3.3 傅里叶级数(Fourier Series)的频谱
- 3.4 傅里叶级数(FS)的相位谱
- 3.5 傅里叶变换(Fourier Tranformation)
- 3.6 欧拉公式
- 3.7 指数形式的傅里叶变换 FT
- 4. 马尔科夫 Markov
-
- 4.1 马尔科夫性质
- 4.2 马尔科夫过程 Markov process
- 4.3 马尔科夫链 Markov Chain
- 4.4 隐马尔科夫 HMM
-
- 4.4.1 模型定义
- 4.4.2 三个基本问题
- 4.4.3 问题1-概率计算:求观测序列的概率
- 4.4.4 问题2-学习问题:估计模型的参数
- 4.4.5 问题3-预测问题:最可能隐藏状态序列求解
- 4.4.6 实际应用
- 4.5 马尔科夫随机场 MRF
- 5. 条件随机场 CRF
-
- 5.1 概率图
-
- 5.1.1 有向图与无向图
- 5.1.2 判别式(discriminative)模型vs生成式(generative)模型
- 5.2 序列建模
- 5.3 CRF的定义与形式
1. 极大似然估计 MLE
本部分参考来源有:千字讲解极大似然估计、极大似然估计、极大似然估计详解、一文彻底读懂【极大似然估计】。
对于一系列观察数据,我们常常可以找到一个具体分布来描述,但不清楚分布的参数。这时候我们就需要用**极大似然估计(Maximum Likelihood Estimate,MLE)**来求解这个分布的参数。换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。
1.1 概念
在很多的机器学习问题种,输入 x x x是一个向量,输出 P ( x ) P(x) P(x)为某一个时间的概率(比如, x x x属于某个类别的概率)。对于一个观测的数据集 D = { x 1 , x 2 , … , x n } D = \{ x_1,x_2,…,x_n\} D={x1,x2,…,xn},每一个 x x x之间都是独立同分布,我们将输入 x x x所满足的概率分布建模为 P ( D , θ ) P(D,θ) P(D,θ),则对新输入的预测为 P ( x ∣ D , θ ) P(x|D,θ) P(x∣D,θ),其中 θ θ θ是一个向量,表示了要估计的模型的所有参数(参数估计的对象)。那么如何求解或者估计出 θ θ θ的值呢?
对于θ的本质不同认识,可以分为频率学派和贝叶斯学派两大派别。
- 频率学派:认为θ是确定的,有一个真实值,目标是找出或者逼近这个真实值;
- 贝叶斯学派:认为θ是不确定的,不存在唯一的真实值,而是服从某一个概率分布。
因此,对于参数估计也有三种不同的方法:
- 极大似然估计:MLE(Maximum Likelihood Estimation)【频率学派】
- 极大后验估计:MAP(Maximum A Posterior)【贝叶斯学派】
- 贝叶斯估计:BE(Bayesian Estimation)【贝叶斯学派】
最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
原理:
极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
1.2 公式
对于一组观测样本 L = ( x 1 , x 2 , … , x n ) L = ( x_1,x_2,…,x_n ) L=(x1,x2,…,xn),其似然函数为: L ( θ ) = L ( x 1 , x 2 , … , x n ; θ ) = ∏ i = 1 n p ( x 1 ; θ ) L(θ) = L(x_1,x_2,…,x_n;θ) = ∏^n_{i=1}p(x_1;θ) L(θ)=L(x1,x2,…,xn;θ)=∏i=1np(x1;θ),称 L ( θ ) L(θ) L(θ)为样本的似然函数。
极大似然估计的原理就是固定样本观测值 ( x 1 , x 2 , … , x n ) ( x_1,x_2,…,x_n ) (x1,x2,…,xn),调整参数 ( θ ) (θ) (θ)使 L ( x 1 , x 2 , … , x n ; θ ) = m a x L ( x 1 , x 2 , … , x n ; θ ′ ) L(x_1,x_2,…,x_n;θ) = max\ L(x_1,x_2,…,x_n;θ') L(x1,x2,…,xn;θ)=max L(x1,x2,…,xn;θ′)。其中, θ ′ θ' θ′称为参数 θ θ θ的极大似然估计值。
极大似然估计公式:
θ M L E = a r g m a x p ( D , θ ) = a r g m a x p ( x 1 , θ ) p ( x 2 , θ ) … p ( x n , θ ) = a r g m a x ∏ i = 1 n p ( x i , θ ) θ_{MLE} = argmax\ p(D, θ) = argmax\ p(x_1,θ)p(x_2,θ)…p(x_n,θ) = argmax\ ∏^n_{i=1}\ p(x_i,θ) θMLE=argmax p(D,θ)=argmax p(x1,θ)p(x2,θ)…p(xn,θ)=argmax i=1∏n p(xi,θ)
转化为对数似然函数方程(简化参数θ的求解,保证了极大似然和极大对数似然的等价):
l n θ M L E = a r g m a x l n ∏ i = 1 n p ( x i , θ ) ln^{θ_{MLE}} = argmax\ ln^{∏^n_{i=1}\ p(x_i,θ)} lnθMLE=argmax ln∏i=1n p(xi,θ)
其损失函数形式 = a r g m i n − l n ∏ i = 1 n p ( x i , θ ) = argmin-ln^{∏^n_{i=1}\ p(x_i,θ)} =argmin−ln∏i=1n p(xi,θ)。
1.3 计算步骤
以正态分布的样本随机变量进行模拟求解,正态分布的公式 f ( x ) = 1 2 π σ e x p − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sqrt{2\piσ}}exp^{-\frac{(x-μ)^2}{2σ^2}} f(x)=2πσ1exp−2σ2(x−μ)2,具体步骤如下:
-
写出似然函数:
L ( θ ) = ∏ i = 1 n f ( x i , θ ) = ∏ i = 1 n 1 2 π σ e x p − ( x − μ ) 2 2 σ 2 = ( 1 2 π σ ) n ∏ i = 1 n e x p − ( x − μ ) 2 2 σ 2 L(θ) = ∏^n_{i=1}\ f(x_i,θ) = ∏^n_{i=1}\ \frac{1}{\sqrt{2\piσ}}exp^{-\frac{(x-μ)^2}{2σ^2}}\\ = (\frac{1}{\sqrt{2\piσ}})^n\ ∏^n_{i=1}\ exp^{-\frac{(x-μ)^2}{2σ^2}} L(θ)=i=1∏n f(xi,θ)=i=1∏n 2πσ1exp−2σ2(x−μ)2=(2πσ1)n i=1∏n exp−2σ2(x−μ)2 -
对似然函数取对数:
l n L ( θ ) = l n ∏ i = 1 n f ( x i , θ ) = − n 2 l n 2 π − n l n σ − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 ln^{L(θ)} = ln^{∏^n_{i=1}\ f(x_i,θ)} = -\frac{n}{2}ln^{2\pi}-nln^{σ}-\frac{1}{2σ^2}\sum^n_{i=1}(x_i-μ)^2 lnL(θ)=ln∏i=1n f(xi,θ)=−2nln2π−nlnσ−2σ21i=1∑n(xi−μ)2 -
计算偏导数,取极值,得方程组:
{ ∂ l n L ( μ , σ 2 ) ∂ μ = 1 σ 2 ∑ i = 1 n ( x i − μ ) = 0 ∂ l n L ( μ , σ 2 ) ∂ σ 2 = − n 2 σ 2 + 1 2 σ 4 ∑ i = 1 n ( x i − μ ) 2 = 0 → { ∑ i = 1 n ( x i − μ ) = 0 σ 2 = 1 n ∑ i = 1 n ( x i − μ ) 2 \begin{cases} \frac{∂ln^{L(μ,σ^2)}}{∂μ} = \frac{1}{σ^2}\sum^n_{i=1}(x_i-μ) = 0\\ \frac{∂ln^{L(μ,σ^2)}}{∂σ^2} = -\frac{n}{2σ^2}+\frac{1}{2σ^4}\sum^n_{i=1}(x_i-μ)^2 = 0 \end{cases}\ →\ \begin{cases} \sum^n_{i=1}(x_i-μ) = 0\\ σ^2=\frac{1}{n}\sum^n_{i=1}(x_i-μ)^2 \end{cases} ⎩⎨⎧∂μ∂lnL(μ,σ2)=σ21∑i=1n(xi−μ)=0∂σ2∂lnL(μ,σ2)=−2σ2n+2σ41∑i=1n(xi−μ)2=0 → {∑i=1n(xi−μ)=0σ2=n1∑i=1n(xi−μ)2 -
联合解似然方程,得:
{ μ ^ = x ˉ = 1 n ∑ i = 1 n x i σ 2 ^ = 1 n ∑ i = 1 n ( x i − x ˉ ) 2 \begin{cases} \widehat{μ} = \bar{x} = \frac{1}{n}\sum^n_{i=1}x_i\\ \widehat{σ^2}=\frac{1}{n}\sum^n_{i=1}(x_i-\bar{x})^2 \end{cases} {μ =xˉ=n1∑i=1nxiσ2 =n1∑i=1n(xi−xˉ)2
μ ^ , σ 2 ^ \widehat{μ},\ \widehat{σ^2} μ , σ2 就是正态分布中 μ , σ 2 μ,\ σ^2 μ, σ2的最大似然估计。
1.4 特点及应用
极大似然估计的特点:
- 比其他估计方法更加简单;
- 收敛性:无偏或者渐近无偏,当样本数目增加时,收敛性质会更好;
- 如果假设的类条件概率模型正确,则通常能获得较好的结果。但如果假设模型出现偏差,将导致非常差的估计结果。
极大似然估计在机器学习的理论算法研究中应用广泛,尤其是涉及到机器学习损失函数最小化时,往往会在似然函数中添加负号,以达到最小化的目的。先研究线性回归时,不仅可以根据MSE建立最小误差函数,也可以从正态分布和极大似然估计的角度进行推导。机器学习算法中使用极大似然估计的算法有朴素贝叶斯、EM算法等。
另外极大似然函数特别擅长于处理与概率相关的问题,因为模型的求解往往就是参数的求解,根据批量的随机样本最大化近似或者模拟现实世界,在应用中使用得比较频繁的往往还是离散型随机变量的似然函数求解,而连续型以正态分布函数较为常见。利用极大似然估计建立的损失函数模型,需要进一步借助梯度下降法来不断的更新迭代参数,来对参数进行求解。
2. 贝叶斯 Bayes
本节主要参考内容:通俗地理解贝叶斯公式(定理)、千字讲解极大似然估计。
贝叶斯定理的发明者托马斯·贝叶斯提出了一个很有意思的假设:“如果一个袋子中共有 10 个球,分别是黑球和白球,但是我们不知道它们之间的比例是怎么样的,现在,仅通过摸出的球的颜色,是否能判断出袋子里面黑白球的比例?”
上述问题可能与我们高中时期所接受的的概率有所冲突,因为你所接触的概率问题可能是这样的:“一个袋子里面有 10 个球,其中 4 个黑球,6 个白球,如果你随机抓取一个球,那么是黑球的概率是多少?”毫无疑问,答案是 0.4。这个问题非常简单,因为我们事先知道了袋子里面黑球和白球的比例,所以很容易算出摸一个求的概率,但是在某些复杂情况下,我们无法得知“比例”,此时就引出了贝叶斯提出的问题。
2.1 贝叶斯定理/公式
下面以通俗易懂的方式描述一下“贝叶斯定理”:通常,事件 A 在事件 B 发生的条件下与事件 B 在事件 A 发生的条件下,它们两者的概率并不相同,但是它们两者之间存在一定的相关性,并具有以下公式(称之为“贝叶斯公式”):
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A)·P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
公式中符号的意义如下:
-
P ( A ) P(A) P(A) 这是概率中最基本的符号,表示A出现的概率。之所以称为“先验”是因为它不考虑任何 B 方面的因素;【先验】
-
P ( B ) P(B) P(B) 表示B出现的概率,也作标准化常量(normalized constant);【先验】
-
P ( B ∣ A ) P(B|A) P(B∣A)是条件概率的符号,表示事件A发生的条件下,事件B发生的概率,它也被称为“似然度”;【似然】
-
P ( A ∣ B ) P(A|B) P(A∣B)是条件概率的符号,表示事件B发生的条件下,事件A发生的概率,这个计算结果也被称为“后验概率”;【后验】
注:后验概率其实可以看做是在给定数据之后更新了的先验概率。
因此,贝叶斯公式可以表示为: 后 验 概 率 = ( 似 然 度 × 先 验 概 率 ) / 标 淮 化 常 量 后验概率 = (似然度 × 先验概率)/ 标淮化常量 后验概率=(似然度×先验概率)/标淮化常量。
比例 P ( B ∣ A ) / P ( B ) P(B|A)/P(B) P(B∣A)/P(B)也有时被称作标淮相似度(standardised likelihood),因此贝叶斯公式还可表示为: 后 验 概 率 = 标 淮 相 似 度 × 先 验 概 率 后验概率 = 标淮相似度 × 先验概率 后验概率=标淮相似度×先验概率。
在具体应用中, B B B代表观测到的数据, A A A代表需要估计的参数(可能是向量)。
贝叶斯公式的应用示例:贝叶斯通俗易懂推导。
2.2 贝叶斯估计的步骤
通用步骤(求 P ( θ ∣ D ) P(θ|D) P(θ∣D)):
-
确定参数 θ θ θ的先验分布 P ( θ ) P(θ) P(θ);
注:伯努利、二项式、负二项式和几何分布参数的共轭先验是Beta分布, 多项式分布参数的共轭先验是Dirichlet分布, 指数分布参数的共轭先验是Gamma分布,高斯分布均值的共轭先验是另一个高斯分布, 泊松分布的共轭先验是Gamma分布。
-
根据观测数据集 D = { x 1 , x 2 , … , x n } D=\{x_1, x_2,…,x_n\} D={x1,x2,…,xn},确定参数 θ θ θ的似然值 P ( D ∣ θ ) P(D|θ) P(D∣θ);
-
确定参数 θ θ θ的后验分布函数 P ( D ) P(D) P(D);
在连续型随机变量中, P ( D ) = ∫ θ P ( D ∣ θ ) ⋅ P ( θ ) ⋅ d θ P(D) = \int_θP(D|θ)·P(θ)·dθ P(D)=∫θP(D∣θ)⋅P(θ)⋅dθ。
-
利用贝叶斯公式,求参数 θ θ θ的后验分布 P ( θ ∣ D ) P(θ|D) P(θ∣D);
-
求出参数 θ θ θ的贝叶斯估计值 θ ^ = ∫ θ θ P ( θ ∣ D ) d θ \hat{θ} = \int_θθP(θ|D)dθ θ^=∫θθP(θ∣D)dθ;
-
估计新测量数据 x ~ \tilde{x} x~出现的概率 P ( x ~ ∣ D ) P(\tilde{x}|D) P(x~∣D)。
贝叶斯估计要解决的不是如何估计参数,而是用来估计新测量数据出现的概率。
以抛硬币为例(二项分布):
-
二项分布参数的共轭先验是Beta分布,由于 θ θ θ的似然函数服从二项分布,因此在贝叶斯估计中,假设 θ θ θ的先验分布服从 P ( θ ) ∽ B e t a ( α , β ) P(θ)\backsim Beta(\alpha, \beta) P(θ)∽Beta(α,β),Beta分布的概率密度公式为( B B B函数,也称 B e t a Beta Beta函数,是一个标准化常量,用来使整个概率的积分为1):
f ( x ; α , β ) = 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 f(x;\alpha, \beta) = \frac{1}{B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta-1} f(x;α,β)=B(α,β)1xα−1(1−x)β−1 -
根据观测数据集 D = { x 1 , x 2 , … , x n } D=\{x_1, x_2,…,x_n\} D={x1,x2,…,xn},可以求得似然值 P ( D ∣ θ ) P(D|θ) P(D∣θ);
-
在连续型随机变量中, P ( D ) = ∫ θ P ( D ∣ θ ) ⋅ P ( θ ) ⋅ d θ P(D) = \int_θP(D|θ)·P(θ)·dθ P(D)=∫θP(D∣θ)⋅P(θ)⋅dθ;
-
根据贝叶斯公式求解后验分布 P ( θ ∣ D ) P(θ|D) P(θ∣D):
P ( θ ∣ D ) = P ( D ∣ θ ) ⋅ P ( θ ) ∫ θ P ( D ∣ θ ) ⋅ P ( θ ) ⋅ d θ = θ 6 ( 1 − θ ) 4 θ α − 1 ( 1 − θ ) β − 1 B ( α , β ) ∫ θ θ 6 ( 1 − θ ) 4 ⋅ θ α − 1 ( 1 − θ ) β − 1 B ( α , β ) d θ = … … = B e t a ( θ ∣ α + 6 , β + 4 ) P(θ|D) = \frac{P(D|θ)·P(θ)}{\int_θP(D|θ)·P(θ)·dθ} = \frac{θ^6(1-θ)^4\frac{θ^{\alpha-1}(1-θ)^{\beta-1}}{B(\alpha, \beta)}}{\int_θθ^6(1-θ)^4·\frac{θ^{\alpha-1}(1-θ)^{\beta-1}}{B(\alpha, \beta)}dθ}\\ =……\\ =Beta(θ|\alpha+6,\beta+4) P(θ∣D)=∫θP(D∣θ)⋅P(θ)⋅dθP(D∣θ)⋅P(θ)=∫θθ6(1−θ)4⋅B(α,β)θα−1(1−θ)β−1dθθ6(1−θ)4B(α,β)θα−1(1−θ)β−1=……=Beta(θ∣α+6,β+4) -
根据Beta分布的数学期望公式 E ( θ ) = α α + β E(θ)=\frac{\alpha}{\alpha+\beta} E(θ)=α+βα,可得参数 θ θ θ的贝叶斯估计值 θ ^ \hat{θ} θ^:
θ ^ = ∫ θ θ P ( θ ∣ D ) d θ = E ( θ ) = α α + β = 9 9 + 7 = 0.5625 \hat{θ} = \int_θθP(θ|D)dθ = E(θ) = \frac{\alpha}{\alpha+\beta} = \frac{9}{9+7} = 0.5625 θ^=∫θθP(θ∣D)dθ=E(θ)=α+βα=9+79=0.5625 -
估计新测量数据 x ~ \tilde{x} x~出现的概率 P ( x ~ ∣ D ) P(\tilde{x}|D) P(x~∣D):
P ( x ~ ∣ D ) = ∫ θ P ( x ~ ∣ θ ) ⋅ P ( θ ∣ D ) ⋅ d θ = ∫ θ P ( x ~ ∣ θ ) ⋅ P ( D ∣ θ ) ⋅ P ( θ ) P ( D ) ⋅ d θ P(\tilde{x}|D) = \int_θP(\tilde{x}|θ)·P(θ|D)·dθ = \int_θP(\tilde{x}|θ)·\frac{P(D|θ)·P(θ)}{P(D)}·dθ P(x~∣D)=∫θP(x~∣θ)⋅P(θ∣D)⋅dθ=∫θP(x~∣θ)⋅P(D)P(D∣θ)⋅P(θ)⋅dθ
共轭先验 Conjugate Prior
「共轭」是数学中一个比较有逼格的词。「轭」是牛拉车用的木头,同时拉一辆车的两头牛,就是「共轭」关系。把这种关系引申到数学中,只要是成对的东西,又找不着一个更合适的叫法时,就常常称它们为「共轭」。“conjugate” means “to become joined together”。
在贝叶斯理论中,如果先验分布和似然函数可以使得先验分布和后验分布有相同的形式,那么就称先验分布与似然函数是共轭的,共轭的结局是让先验与后验具有相同的形式。
之所以采用共轭先验的原因是可以使得先验分布和后验分布的形式相同,这样一方面合符人的直观(它们应该是相同形式的)另外一方面是可以形成一个先验链,即现在的后验分布可以作为下一次计算的先验分布,如果形式相同,就可以形成一个链条。
2.3 朴素贝叶斯 Naive Bayes
朴素贝叶斯是一种十分简单的分类算法,其基本思想:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。
朴素贝叶斯分类器的一个重要假定:分类对应的各个属性间是相互独立的(这也是“朴素Naive”一词的由来)。
然而在现实应用中,这个往往难以做到,那怎么办呢?
很简单,适当考虑一部分属性间的相互依赖关系,这种放松后的分类称为半朴素贝叶斯分类,其中最常用的策略:假定每个属性仅依赖于其他最多一个属性,称其依赖的这个属性为其超父属性,这种关系称为:独依赖估计(ODE)。
补充:贝叶斯网络的概念。
2.4 贝叶斯优化 Bayesian Optimization
本节主要参考内容:贝叶斯优化与SMBO、高斯过程回归、TPE、
在开始前,我们先厘清以下几个该领域常见的、容易混淆的概念:AutoML, Bayesian Optimization (BO), Sequential Model Based Optimisation (SMBO), Gaussian Process Regression (GPR), Tree Parzen Estimator (TPE)。
AutoML是最大的一个概念,涵盖了贝叶斯优化(Bayesian Optimization, BO)、神经结构搜索( Neural Architecture Search, NAS)以及很多工程性的东西。AutoML的目标就是让没有机器学习(这里包括深度学习)经验的人,可以使用某一个平台来构造、训练、使用机器学习模型,这个平台负责进行数据管理、模型结构设计、模型超参数调节(hyper-parameter tuning)、模型的评估与使用等等。
贝叶斯优化(BO)则是AutoML中进行超参数调节的一种先进的方法,并列于人工调参(manul)、网格搜索(Grid Search)、随机搜索(Rrandom Search)。
SMBO则是贝叶斯优化的一种具体实现方法,是一种迭代式的优化方法,每一次的迭代就是一次新的超参数组合实验,而每次的迭代都是基于前面的历史。其实SMBO可以认为就是BO的标准实现,二者在很多语境下我感觉是可以等价的。
最后就是Gaussian Process Regression (GPR) 和Tree Parzen Estimator (TPE) 了,这俩玩意儿是并列的概念,是SMBO方法中的两种建模策略。
2.4.1 超参数调节方法
超参数调节(hyper-parameter tuning),主要有下面四种方法:人工调参(manul tuning)、网格搜索(grid search)、随机搜索(random search)、贝叶斯优化(Bayesian Optimization)。
人工调参就是基于人的经验去调整参数。现在简单对比一下grid search(左图)和random search(右图):
random search在相同的超参数组合次数中,探索了更多的空间(这句话也有歧义,更准确得说应该是每个维度的参数,都尝试了更多的可能),因此从平均意义上看可以比grid search更早得找到较好的区域。从理论上将,random search可以更快地将整个参数空间都覆盖到,而不是像grid search一样从局部一点点去搜索。
但是,grid search和random search,都属于无先验式的搜索,有些地方称之为Uninformed search,即每一步的搜索,都不考虑已经探索的点的情况,这也是grid/random search的主要问题,都是“偷懒式”搜索,闭着眼睛乱找一通。
而贝叶斯优化,则是一种informed search,会利用前面已经搜索过的参数的表现,来推测下一步怎么走会比较好,从而减少搜索空间,大大提升搜索效率。 某种意义上,贝叶斯优化跟人工调参比较像,因为我们调参师傅也会根据已有的结果以及自己的经验来判断下一步如何调参。
2.4.2 SMBO算法
假设一组超参数组合是 X = x 1 , x 2 , . . . , x n X=x_1,x_2,...,x_n X=x1,x2,...,xn( x n x_n xn表示某一个超参数的值),不同超参数会得到不同效果,贝叶斯优化假设超参数与最后我们需要优化的损失函数存在一个函数关系。
贝叶斯优化的大体思路如下:假设我们有一个函数 f : x → R f:x→R f:x→R,我们需要在 x ⊆ X x⊆X x⊆X内找到 x ∗ = a r g m i n f ( x ) x^* = argmin\ f(x) x∗=argmin f(x)。( x x x表示的是超参数,而不是输入数据; f f f是损失函数)
SMBO全名Sequential model-based optimization,序列化基于模型的优化。所谓序列化,是指通过迭代的方式,通过一次一次试验来进行优化。是贝叶斯优化的最简形式。SMBO的框架如下(SMBO框架伪代码):

其中各个符号的意思如下:
- f f f是我们要去优化的函数, x x x是超参数组合,比方我们要训练一个图片分类模型,那么每一个 x x x的选择,都会对应该分类模型的一个损失,这个函数关系就是 f f f。一般, f f f的计算都是十分耗时的;
- S S S是surrogate的缩写,意为“代理”,我们使用 S S S作为 f f f的代理函数,一般通过最小化 S S S来寻找下一步超参数怎么选, S S S的计算一般会容易得多。一般这一步的最小化,我们是通过最大化一个acquisition function来进行的;
- H H H是history,是前面所有的 { x , f ( x ) } \{x,f(x)\} {x,f(x)}的记录,我们要对 H H H进行建模,得到它们的概率分布模型 M M M。
总体步骤如下:
- 根据已有的调参历史 H = ( x 1 : k , f ( x 1 : k ) ) H = (x_{1:k},f(x_{1:k})) H=(x1:k,f(x1:k)),建立概率分布模型 M M M;
- 根据acquisition function来挑选下一步超参数 x k + 1 x_{k+1} xk+1;
- 将新的观测 ( x k + 1 , f ( x k + 1 ) ) (x_{k+1},f(x_{k+1})) (xk+1,f(xk+1))加入到 H H H中;
- 重复1-3步骤,直到达到最大迭代数。
所以,不同的贝叶斯优化方法,主要区别在:用何种概率模型对历史进行建模、acquisition function如何选。
所以,贝叶斯优化中的一个关键步骤,就是对要优化的目标函数进行建模,得到该函数的分布 p ( y ∣ x ) p(y|x) p(y∣x),从而了解该函数可能会在什么范围内波动。有了函数的分布,实际上也就有了y在给定x的时候的条件分布。具体的建模方法,最经典的包括高斯过程回归(GPR)和Tree Parzen Estimator(TPE),在2.4.4节。
2.4.4 Expected Improvement (EI)
有了建模方法,现在我们该如何根据目标函数的分布,来选择下一个超参数呢?
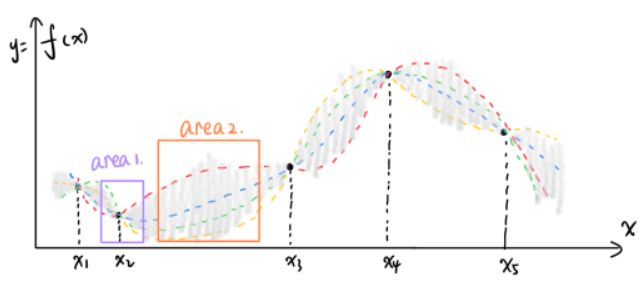
已经观测到的点中,是 x 2 x_2 x2最佳的超参数,那我们下一个点往哪个方向找?我们有两种策略:
- Exploitation(剥削?挖掘?使劲利用?):我们既然发现了 x 2 x_2 x2最好,那估计周围的点也不错,所以我们在图中的area 1里面搜索;
- Exploration(探索):虽然 x 2 x_2 x2处目前来看比较好,但是我们还没有探索到的空间实际还有好多好多,比方说图中的area 2区域,这里面很可能藏着惊喜!
实际上,上面两种策略各有各的道理,我们需要设计一个acquisition function来帮我们进行判断。一种最常用的方案就是Expected Improvement (EI),它是对Exploration和Exploitation做了一个折中。Expected Improvement (EI)的公式如下:
也就是,我们首先有一个baseline—— y ∗ y^* y∗,我们就是通过计算EI——相对于 y ∗ y^* y∗的期望提升,来评价一个超参数的好坏。所以,我们下一步要找的超参数,就是: x n e w = a r g m a x x E I y ∗ ( x ) x_{new}=argmax_xEI_{y^*}(x) xnew=argmaxxEIy∗(x)。
EI的公式决定了其偏好于选择均值小的、方差大的区域,因此就体现了"exploration vs. exploitation trade-off"。
2.4.3 不同概率分布的建模策略
① 基于GPR的贝叶斯优化;② 基于TPE的贝叶斯优化。具体介绍可见:通俗科普文:贝叶斯优化与SMBO、高斯过程回归、TPE。
从论文的实验中,发现TPE的总体效果会比GPR更好。具体原因,论文也只是给了一些猜测:TPE的建模相对于GPR可能更加准确,另外对于阈值的更加保守的选择可能是一个更好的先验。但是这仅仅是论文的两个数据集上的实验,实际上各种开源的工具都有不同的选择,有些选择GPR,有些选择TPE还有其他算法的。另外,成熟的工具一般还对改论文的方法做了一些改进,比如如何进行更好的初始化等等。
2.4.4 Python应用
贝叶斯优化的优点:
- 贝叶斯调参采用高斯过程,考虑之前的参数信息,不断地更新先验;网格搜索未考虑之前的参数信息;
- 贝叶斯调参迭代次数少,速度快;网格搜索速度慢,参数多时易导致维度爆炸;
- 贝叶斯调参针对非凸问题依然稳健;网格搜索针对非凸问题易得到局部优最。
具体应用而言,有看到了两个库和一些使用教程,分别是bayes_opt(贝叶斯优化器、贝叶斯优化python实现)和Hyperopt(调参神器hyperopt)库。
3. 傅里叶分析 Fourier
本节主要参考:深入浅出的讲解傅里叶变换、彻底理解傅里叶变换。
3.1 什么是频域
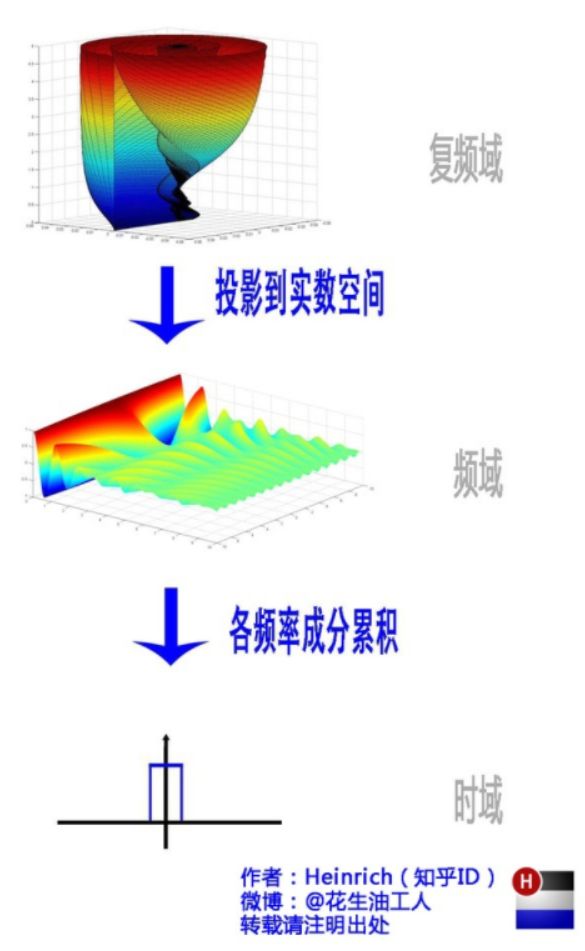
从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析(时序分析)。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。
在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。
所以,你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。抱歉,这不是一句鸡汤文,而是黑板上确凿的公式:傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。在第一个例子里我们可以理解为,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。
而贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation),我们从简单的开始谈起。
3.2 傅里叶变换是什么
简而言之,傅里叶变换把一个输入信号分解成一堆正弦波的叠加。就像大多数数学方法一样,这个名字来自一个名叫傅立叶的人。让我们从一些简单的例子开始,然后继续前进。首先,我们来看看什么是波 —— 波随着时间的推移,一直按照某一规律变化。
这是一个波的例子:
这个波可以分解为两个正弦波的叠加。也就是说,当我们将两个正弦波相加时,就会得到原来的波。

傅里叶变换可以让我们从一个复杂的波形里面,把构成这个波的单个正弦波分离出来。在这个例子中,你几乎可以通过“脑补”完成这一操作。为什么?事实证明,现实世界中的许多事物间的互相交互,都是基于正弦波。我们通常将这种波的快慢的性质,称为波的频率。
最明显的例子就是声音 —— 当我们听到声音时,我们听不到那条波浪线,但我们听到构成声音的正弦波的不同频率。能够在计算机上区分这两个音调,我们就可以了解一个人实际可以听到的内容。我们可以理解声音的高低,或弄清楚这个波包含了什么音符。
一些波看起来不像由正弦波构成,我们也可以用这个分解的过程来进行分析。
3.3 傅里叶级数(Fourier Series)的频谱
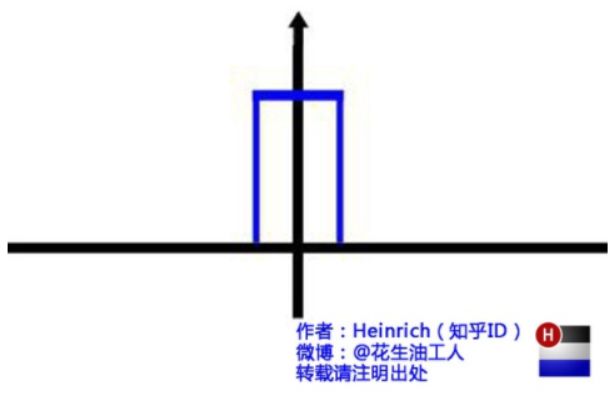
我们来看看这个家伙吧。这个波称为方波。

虽然看起来不太可能,但它确实也可以分解成正弦波。

随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准 90 度角的矩形波呢?不幸的告诉大家,答案是无穷多个。
不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点,但是一旦接受了这样的设定,游戏就开始有意思起来了。还是上图的正弦波累加成矩形波,我们换一个角度来看看:
在这几幅图中,最前面黑色的线就是所有正弦波叠加而成的总和,也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅都是不同的。一定有细心的读者发现了,每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为 0 的正弦波!也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。
这里,不同频率的正弦波我们称为频率分量。
**好了,关键的地方来了!!**如果我们把第一个频率最低的频率分量看作“1”,我们就有了构建频域的最基本单元。时域的基本单元就是“1 秒”,如果我们将一个角频率为![]() 的正弦波 cos(
的正弦波 cos(![]() t)看作基础,那么频域的基本单元就是
t)看作基础,那么频域的基本单元就是![]() 。有了“1”,还要有“0”才能构成世界,那么频域的“0”是什么呢?cos(0t)就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0 频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
。有了“1”,还要有“0”才能构成世界,那么频域的“0”是什么呢?cos(0t)就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0 频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
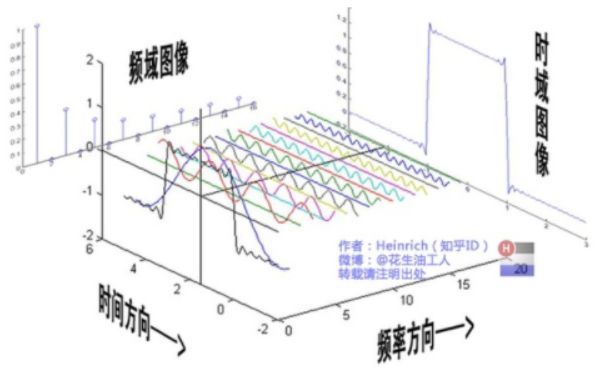
介绍完了频域的基本组成单元,我们就可以看一看一个矩形波,在频域里的另一个模样了:
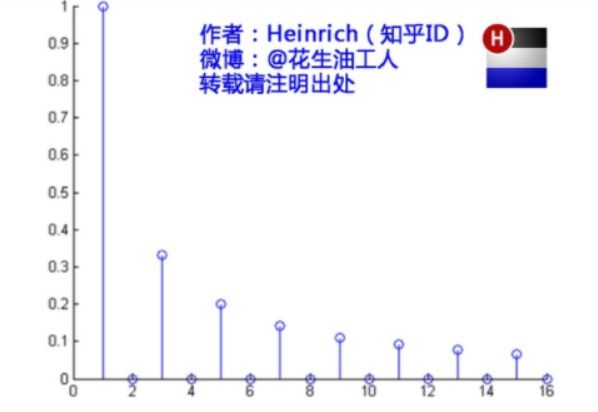
这是什么奇怪的东西?这就是矩形波在频域的样子,是不是完全认不出来了?教科书一般就给到这里然后留给了读者无穷的遐想,以及无穷的吐槽,其实教科书只要补一张图就足够了:频域图像,也就是俗称的频谱,就是——
再清楚一点:
可以发现,在频谱中,偶数项的振幅都是0,也就对应了图中的彩色直线。振幅为 0 的正弦波。
3.4 傅里叶级数(FS)的相位谱
上一章的关键词是:从侧面看。这一章的关键词是:从下面看。
在这一章最开始,我想先回答很多人的一个问题:傅里叶分析究竟是干什么用的?
先说一个最直接的用途。无论听广播还是看电视,我们一定对一个词不陌生——频道。频道频道,就是频率的通道,不同的频道就是将不同的频率作为一个通道来进行信息传输。下面大家尝试一件事:
先在纸上画一个sin(x),不一定标准,意思差不多就行。不是很难吧。好,接下去画一个sin(3x)+sin(5x)的图形。别说标准不标准了,曲线什么时候上升什么时候下降你都不一定画的对吧?好,画不出来不要紧,我把sin(3x)+sin(5x)的曲线给你,但是前提是你不知道这个曲线的方程式,现在需要你把sin(5x)给我从图里拿出去,看看剩下的是什么。这基本是不可能做到的。但是在频域呢?则简单的很,无非就是几条竖线而已。
所以很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
再说一个更重要,但是稍微复杂一点的用途——求解微分方程。微分方程的重要性不用我过多介绍了。各行各业都用的到。但是求解微分方程却是一件相当麻烦的事情。因为除了要计算加减乘除,还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法,大学数学瞬间变小学算术有没有。傅里叶分析当然还有其他更重要的用途,我们随着讲随着提。
下面我们继续说相位谱:
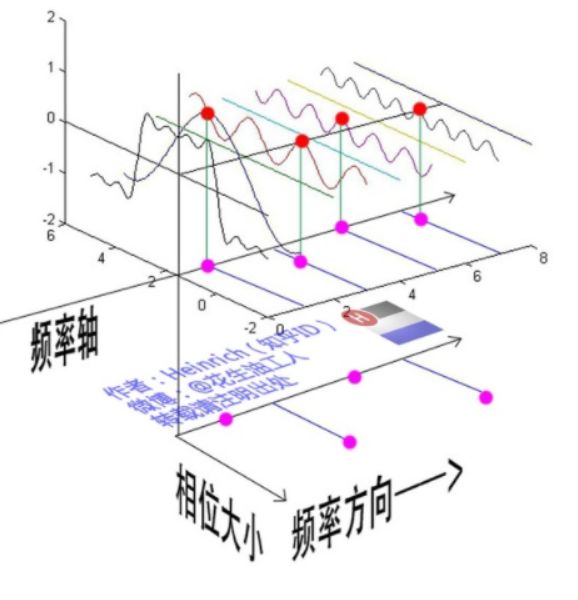
通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。基础的正弦波A.sin(wt+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。那么这个相位谱在哪呢?我们看下图,这次为了避免图片太混论,我们用7个波叠加的图。
鉴于正弦波是周期的,我们需要设定一个用来标记正弦波位置的东西。在图中就是那些小红点。小红点是距离频率轴最近的波峰,而这个波峰所处的位置离频率轴有多远呢?为了看的更清楚,我们将红色的点投影到下平面,投影点我们用粉色点来表示。当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。
这里需要纠正一个概念:时间差并不是相位差。如果将全部周期看作2Pi或者360度的话,相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi,就得到了相位差。
在完整的立体图中,我们将投影得到的时间差依次除以所在频率的周期,就得到了最下面的相位谱。所以,频谱是从侧面看,相位谱是从下面看。
注意到,相位谱中的相位除了0,就是Pi。因为cos(t+Pi)=-cos(t),所以实际上相位为Pi的波只是上下翻转了而已。对于周期方波的傅里叶级数,这样的相位谱已经是很简单的了。另外值得注意的是,由于cos(t+2Pi)=cos(t),所以相位差是周期的,pi和3pi,5pi,7pi都是相同的相位。人为定义相位谱的值域为(-pi,pi],所以图中的相位差均为Pi。
3.5 傅里叶变换(Fourier Tranformation)
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的。
在这个世界上,有的事情一期一会,永不再来,并且时间始终不曾停息地将那些刻骨铭心的往昔连续的标记在时间点上。但是这些事情往往又成为了我们格外宝贵的回忆,在我们大脑里隔一段时间就会周期性的蹦出来一下,可惜这些回忆都是零散的片段,往往只有最幸福的回忆,而平淡的回忆则逐渐被我们忘却。因为,往昔是一个连续的非周期信号,而回忆是一个周期离散信号。是否有一种数学工具将连续非周期信号变换为周期离散信号呢?抱歉,真没有。
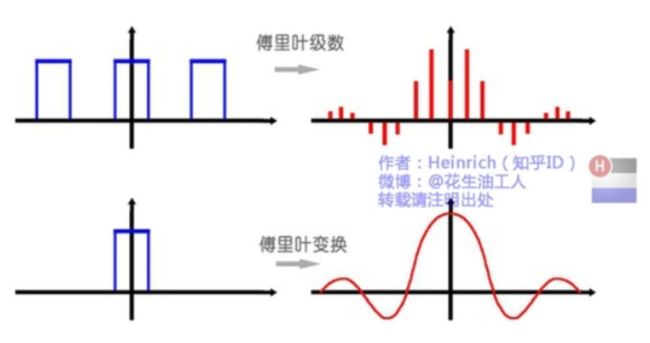
比如傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。而在我们接下去要讲的傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号。上一张图方便大家理解吧:
或者我们也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。因此在傅里叶变换在频域上就从离散谱变成了连续谱。那么连续谱是什么样子呢?
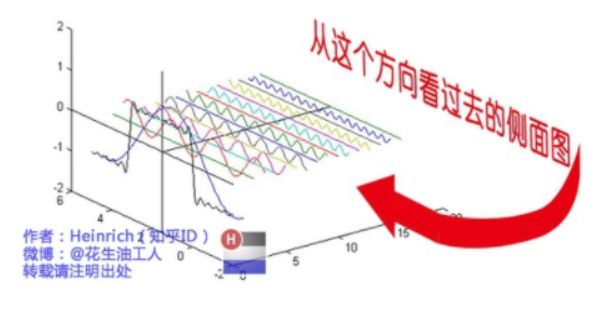
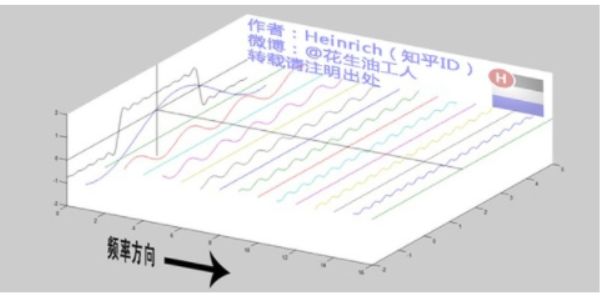
为了方便大家对比,我们这次从另一个角度来看频谱,还是傅里叶级数中用到最多的那幅图,我们从频率较高的方向看。
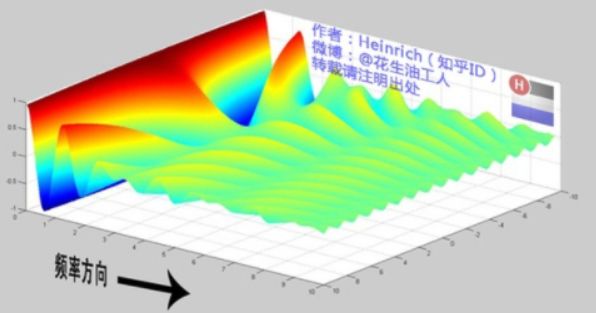
以上是离散谱,那么连续谱是什么样子呢?尽情的发挥你的想象,想象这些离散的正弦波离得越来越近,逐渐变得连续……直到变得像波涛起伏的大海:
原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。
3.6 欧拉公式
虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1 的平方根,可是它真正的意义是什么呢?
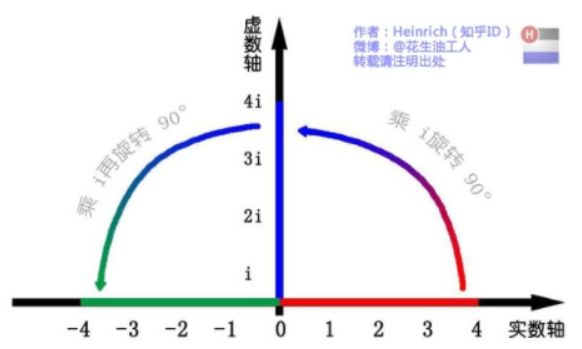
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以 3 的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1 的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了 180 度。
我们知道乘-1 其实就是乘了两次 i 使线段旋转了 180 度,那么乘一次 i 呢——答案很简单——旋转了 90 度。
同时,我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面,也称复平面。这样我们就了解到,乘虚数i的一个功能——旋转。
欧拉公式: e i x = c o s x + i ⋅ s i n x e^{ix} = cosx + i·sinx eix=cosx+i⋅sinx。当x等于 Pi 的时候: e i π + 1 = 0 e^{i\pi} + 1 = 0 eiπ+1=0。这个公式关键的作用,是将正弦波统一成了简单的指数形式。我们来看看图像上的涵义:
欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
3.7 指数形式的傅里叶变换 FT
有了欧拉公式的帮助,我们便知道:正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。而螺旋线的叠加如果用一个形象的栗子来理解是什么呢?光波。
所以其实我们在很早就接触到了光的频谱,只是并没有了解频谱更重要的意义。但不同的是,傅里叶变换出来的频谱不仅仅是可见光这样频率范围有限的叠加,而是频率从 0 到无穷所有频率的组合。
这里,我们可以用两种方法来理解正弦波:第一种前面已经讲过了,就是螺旋线在实轴的投影。另一种需要借助欧拉公式的另一种形式去理解(右式由左式相加再除2得到):
这个式子可以怎么理解呢?我们刚才讲过, e i t e^{it} eit可以理解为一条逆时针旋转的螺旋线,那么 e − i t e^{-it} e−it则可以理解为一条顺时针旋转的螺旋线。而 c o s ( t ) cos (t) cos(t)则是这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了!
这里,逆时针旋转的我们称为正频率,而顺时针旋转的我们称为负频率(注意不是复频率)。
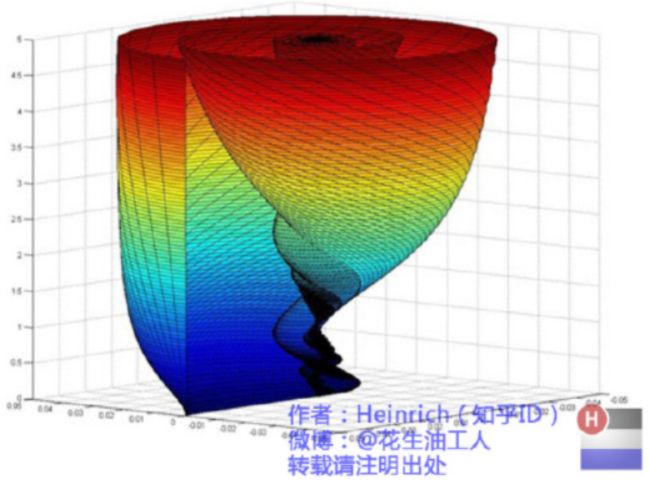
刚才我们已经看到了大海——连续的傅里叶变换频谱,现在想一想,连续的螺旋线会是什么样子:
是不是很漂亮?你猜猜,这个图形在时域是什么样子?
是不是觉得被狠狠扇了一个耳光。数学就是这么一个把简单的问题搞得很复杂的东西。顺便说一句,那个像大海螺一样的图,为了方便观看,我仅仅展示了其中正频率的部分,负频率的部分没有显示出来。如果你认真去看,海螺图上的每一条螺旋线都是可以清楚的看到的,每一条螺旋线都有着不同的振幅(旋转半径),频率(旋转周期)以及相位。而将所有螺旋线连成平面,就是这幅海螺图了。
好了,讲到这里,相信大家对傅里叶变换以及傅里叶级数都有了一个形象的理解了,我们最后用一张图来总结一下:
其实看完博主的这篇博客后,我觉得并不能完全地理解傅里叶分析,但相比之前——连它是什么都不知道,到现在或多或少了解了一点概念含义来说,已经有很大的进步了。或许之后真正遇到需要用傅里叶分析的时候,才会更深入地去了解这个东西(话说这种可能性不大)。
另外,傅里叶和神经网络的关系也有看到过这样一篇文章:相较神经网络,大名鼎鼎的傅里叶变换,为何没有一统函数逼近器?。
4. 马尔科夫 Markov
本节参考内容:初识马尔科夫模型、马尔科夫模型 Markov Model、隐马尔可夫模型、小孩都看得懂的 HMM、
马尔科夫模型(Markov Model)由安德烈·马尔可夫(1856-1922)发明,是数学中具有马尔科夫性质的离散时间随机过程。该过程具有如下特性:在已知目前状态(现在)的条件下,它未来的演变(将来)不依赖于它以往的演变 (过去 )。
马尔科夫模型是一个很大的概念,从模型的定义和性质来看,具有马尔科夫性质、并以随机过程为基础模型的随机过程/随机模型被统称为马尔科夫模型,其中就包含我们悉知的马尔科夫链、马尔科夫决策过程、隐马尔科夫链(HMM)等随机过程/随机模型。
马尔可夫模型是一种统计模型,广泛应用在语音识别,词性自动标注,音字转换,概率文法、序列分类等各个自然语言处理等应用领域。经过长期发展,尤其是在语音识别中的成功应用,使它成为一种通用的统计工具。到目前为止,它一直被认为是实现快速精确的语音识别系统的最成功的方法之一。
4.1 马尔科夫性质
要理解马尔科夫性质,需要了解生成模式(Generating Patterns),一般来说有以下两种生成模式:
-
确定性模式(Deterministic Patterns)→ 确定性系统
- 考虑一套交通信号灯,灯的颜色变化序列依次是红色-红色/黄色-绿色-黄色-红色。这个序列可以作为一个状态机器,交通信号灯的不同状态都紧跟着上一个状态;
-
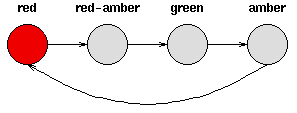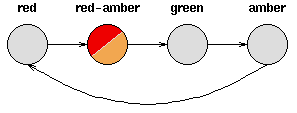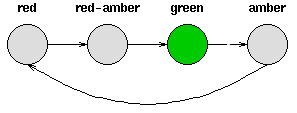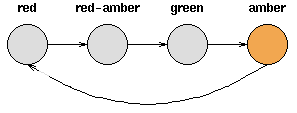
- 注意每一个状态都是唯一的依赖于前一个状态,所以,如果交通灯为绿色,那么下一个颜色状态将始终是黄色——也就是说,该系统是确定性的;
- 确定性系统相对比较容易理解和分析,因为状态间的转移是完全已知的。
-
非确定性模式(Non-deterministic patterns)→ 马尔科夫
-
考虑最经典的赌徒输光例子。赌徒在赌场赌博,赢的概率是P,输的概率(1-P),每次的赌注为1元,假设赌徒最开始时有赌金n元,赢了赌金加1元,输了赌金减1元。问赌徒输光的概率是多少?
-
假设赌徒有两个过程:
- 赌徒1过程: 0 → 1 → 2 → 1 → ?
- 赌徒2过程: 0 → 1 → ?
-
这里两种过程输光的概率一样,不关乎前面的过程,只关乎现在只有一块钱。这就是马尔科夫性,也称为无后效性。简单地说就是将来与过去无关,只与现在有关,不断向前形成这样一个过程。
这里的“现在”,在应用过程中,可以不仅仅单指当前一个时刻 t t t,还能拓展理解:比如第 i i i时刻上的取值仅依赖于第 ( i − n ) (i-n) (i−n)时刻的取值。
-
4.2 马尔科夫过程 Markov process
若随机过程满足马尔可夫性,则称为马尔可夫过程。 在该模型中,存在两个假设:① 随机过程满足马尔可夫性性;② 状态转移矩阵不随时间的变化而变化。
对于有 M M M个状态的一阶马尔科夫模型,共有 M 2 M^2 M2个状态转移,因为任何一个状态都有可能是所有状态的下一个转移状态。每一个状态转移都有一个概率值,称为状态转移概率——这是从一个状态转移到另一个状态的概率。所有的 M 2 M^2 M2个概率可以用一个状态转移矩阵表示。注意这些概率并不随时间变化而不同——这是一个非常重要(但常常不符合实际)的假设。
下面的状态转移矩阵显示的是天气例子中可能的状态转移概率:

一个马尔科夫过程就是指过程中的每个状态的转移只依赖于之前的n个状态,这个过程被称为n阶马尔科夫模型,其中n是影响转移状态的数目。最简单的马尔科夫过程就是一阶过程,每一个状态的转移只依赖于其之前的那一个状态(也称为齐次马尔科夫链假设),这也是后面很多模型的讨论基础。
对于一阶马尔科夫模型,则有:如果第i时刻上的取值依赖于且仅依赖于第i−1时刻的取值,即:
P ( x i ∣ x i − 1 , x i − 2 , … , x 1 ) = P ( x i ∣ x i − 1 ) P(x_i|x_{i-1}, x_{i-2},…,x_1) = P(x_i|x_{i-1}) P(xi∣xi−1,xi−2,…,x1)=P(xi∣xi−1)
马尔科夫模型与时间序列的关系与区别:
马尔科夫模型与时间序列是有一定的关系,有时候甚至有人说马尔科夫过程的状态序列就是一个时间序列,的确,从时间的推移角度来说,这么说好像没很么问题,但是它们之间还是有很多区别的:
- 马尔科夫模型是概率模型。每一个时间点的观测值体现为状态值,所谓状态值就是某一个类别的概率,这跟时间序列显然不一样;
- 马尔科夫模型当前状态与之前状态的关系是通过转移概率、转移概率矩阵来决定的,这也是和时间序列不一样的地方。
4.3 马尔科夫链 Markov Chain
时间和状态都是离散的马尔科夫过程称为马尔科夫链,记为: X n = X ( n ) , n = 0 , 1 , 2 … X_n = X(n),\ n=0,1,2… Xn=X(n), n=0,1,2…,马尔可夫链是随机变量 X 1 , X 2 . X 3 … X_1,X_2.X_3… X1,X2.X3…的一个数列。
这种离散的情况其实就是我们所讨论的重点,很多时候我们就直接说这样的离散情况就是一个马尔科夫模型。
- 状态空间:马尔可夫链是随机变量 X 1 , X 2 . X 3 … X_1,X_2.X_3… X1,X2.X3…的一个数列,每一个变量 X i X_i Xi都有几种不同的可能取值,即他们所有可能取值的集合,被称为“状态空间”,而 X n X_n Xn的值则是在时间 n n n的状态;
- 转移概率 Transition Probability:把在前一时刻某取值下当前时刻取值的条件概率称作转移概率,可以写为(表示在前一个状态为 s s s的条件下,当前状态为 t t t的概率是多少): P s t = P ( x i = t ∣ x i − 1 = S ) P_{st} = P(x_i=t|x_{i-1}=S) Pst=P(xi=t∣xi−1=S);
- 转移概率矩阵:由于在每一个不同的时刻状态不止一种,所以由前一个时刻的状态转移到当前的某一个状态有几种情况,那么所有的条件概率会组成一个矩阵,这个矩阵就称之为“转移概率矩阵”: P = [ P i j ] n ∗ n P=[P_{ij}]_{n*n} P=[Pij]n∗n,其中 P i j P_{ij} Pij表示在时刻t处于状态 i i i,在下一时刻 t + 1 t+1 t+1处于状态 j j j的概率, n n n是系统所有可能的状态个数;
- 初始概率分布:马尔科夫链也包含了每个状态的初始概率,即: Q = [ q 1 , q 2 , … q n ] Q=[q_1,q_2,…q_n] Q=[q1,q2,…qn],其中 q i q_i qi是系统在初始时刻处于状态 i i i的概率。
如下图的马尔科夫链,状态用圆表示,边表示状态的转移概率。
马尔科夫链也包含了每个状态的初始概率,称为马尔科夫链的初始状态向量,向量的大小与状态数相等,如下图的初始状态向量:
状态转移分布和状态的初始分布是马尔科夫链的两个基本属性。
马尔科夫链收敛条件:马尔科夫链模型是否收敛取决于状态转移矩阵:
则称为马尔科夫链收敛。(马尔科夫链的收敛性使我们可以用马尔科夫链采样得到我们需要的样本集,马尔科夫链的无记忆性是隐马尔可夫模型和条件随机场的理论基础)
转移矩阵的限制:
- 马尔科夫链的状态转换不是循环的(非周期性),如果循环则永远不会收敛;
- 任何两个状态是连通的,即状态转移矩阵没有为0的项;
- 状态数是有限的;
- 状态间的转移概率需要固定不变。
4.4 隐马尔科夫 HMM
看到这一部分的时候因为有点其他的事,所以没有细看,只转载了详细讲解 HMM这篇博客,后续可以再仔细看看。
隐马尔科夫模型(Hidden Markov Model,HMM)是比较经典的机器学习模型了,它在语言识别,自然语言处理,模式识别等领域得到广泛的应用。当然,随着目前深度学习的崛起,尤其是RNN,LSTM等神经网络序列模型的火热,HMM的地位有所下降。但是作为一个经典的模型,学习HMM的模型和对应算法,对我们解决问题建模的能力提高以及算法思路的拓展还是很好的。
使用隐马尔可夫模型(HMM)时我们的问题一般有这两个特征:
- 问题是基于序列的,比如时间序列,或者状态序列。
- 问题中有两类数据,一类序列数据是可以观测到的,即观测序列;而另一类数据是不能观察到的,即隐藏状态序列,简称状态序列。
有了这两个特征,那么这个问题一般可以用HMM模型来尝试解决。这样的问题在实际生活中是很多的。比如:我在和你说话,我发出的一串连续的声音就是观测序列,而我实际要表达的一段话就是状态序列,你大脑的任务,就是从这一串连续的声音中判断出我最可能要表达的话的内容。
由于可以观察到的状态序列和隐藏的状态序列是概率相关的,于是我们可以将这种类型的过程建模为有一个隐藏的马尔科夫过程和一个与这个隐藏马尔科夫过程概率相关的并且可以观察到的状态集合,这就是隐马尔可夫模型。
4.4.1 模型定义
HMM 有四个重要的概念:观测值(observation)、隐藏状态(hidden)、转换概率(transition probability)和输出概率(emission probability)。
简单来说,隐马尔科夫 = 马尔科夫链 + 一组观测值。具体内容如下(来自:详细讲解 HMM):

4.4.2 三个基本问题
- 概率计算问题:给定模型 λ = ( A , B , π ) λ = ( A , B , π ) λ=(A,B,π)和观测序列 O = ( o 1 , o 2 , . . . , o T ) O=(o_1,o_2,...,o_T) O=(o1,o2,...,oT)计算在模型 λ λ λ下观测序列为 O O O的概率 P ( O ∣ λ ) P ( O ∣ λ ) P(O∣λ);
- 学习问题:已知观测序列 O = ( o 1 , o 2 , . . . , o T ) O=(o_1,o_2,...,o_T) O=(o1,o2,...,oT),估计模型 λ = ( A , B , π ) λ = ( A , B , π ) λ=(A,B,π)的参数,使得在该模型下观测序列概率 P ( O ∣ λ ) P ( O ∣ λ) P(O∣λ)最大;
- 预测问题/解码问题:已知模型 λ = ( A , B , π ) λ = ( A , B , π ) λ=(A,B,π)和观测序列 O = ( o 1 , o 2 , . . . , o T ) O=(o_1,o_2,...,o_T) O=(o1,o2,...,oT),求对给定的观测序列概率 P ( I ∣ O ) P ( I ∣ O ) P(I∣O)的最大值。即给定观测序列,求最有可能的对应状态序列。
4.4.3 问题1-概率计算:求观测序列的概率

前向后向算法是前向算法和后向算法的统称,这两个算法都可以用来求HMM观测序列的概率。
前向算法本质上属于动态规划的算法,也就是我们要通过找到局部状态递推的公式,这样一步步的从子问题的最优解拓展到整个问题的最优解。


熟悉了用前向算法求HMM观测序列的概率,现在我们再来看看怎么用后向算法求HMM观测序列的概率。后向算法和前向算法非常类似,都是用的动态规划,唯一的区别是选择的局部状态不同,后向算法用的是“后向概率”,那么后向概率是如何定义的呢?


4.4.4 问题2-学习问题:估计模型的参数
接下来会讨论HMM模型参数求解的问题,这个问题在HMM三个问题里算是最复杂的。在研究这个问题之前,建议先阅读EM算法原理总结、人人都能看懂的EM算法推导,这些在本篇里会用到。
鲍姆-韦尔奇算法原理:

利用我们在隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率里第二节中前向概率的定义可得:
鲍姆-韦尔奇算法流程总结:
4.4.5 问题3-预测问题:最可能隐藏状态序列求解
下面我们会讨论HMM模型最后一个问题的求解,即即给定模型和观测序列,求给定观测序列条件下,最可能出现的对应的隐藏状态序列。HMM模型的解码问题最常用的算法是维特比算法,当然也有其他的算法可以求解这个问题。同时维特比算法是一个通用的求序列最短路径的动态规划算法,也可以用于很多其他问题,比如之前讲到的文本挖掘的分词原理中我们讲到了单独用维特比算法来做分词。
下面关注于用维特比算法来解码HMM的的最可能隐藏状态序列。
在HMM中,维特比算法定义了两个局部状态用于递推。维特比算法概述:
维特比算法流程总结:
4.4.6 实际应用
从实践的角度,可以通过Python的hmmlearn库进行HMM的使用(见:hmmlearn使用简介)。
4.5 马尔科夫随机场 MRF
本部分请主要阅读:概率图–马尔可夫随机场(MRF)。
概率图模型(Probabilistic graphical model,PGM)是由图表示的概率分布。概率无向图模型(Probabilistic undirected graphical model)又称马尔可夫随机场(Markov random field),表示一个联合概率分布,其标准定义为:
设有联合概率分布 P(V) 由无向图 G=(V, E) 表示,图 G 中的节点表示随机变量,边表示随机变量间的依赖关系。如果联合概率分布 P(V) 满足成对、局部或全局马尔可夫性,就称此联合概率分布为概率无向图模型或马尔可夫随机场。
设有一组随机变量 Y ,其联合分布为 P(Y) 由无向图 G=(V, E) 表示。图 G 的一个节点 v∈V表示一个随机变量 YvYv ,一条边 e∈E就表示两个随机变量间的依赖关系。
马尔可夫随机场(MarkovRandom Field,MRF)是典型的马尔可夫网络,图中每个结点表示一个或一组变量,结点之间的边表示两个变量之间的依赖关系。
马尔可夫随机场是一种具有马尔可夫性的随机场,要理解什么是马尔可夫随机场,我们得要先理解什么是随机场。
在概率论中,由样本空间Ω = {0, 1, …, G − 1}n取样构成的随机变量Xi所组成的S = {X1, …, Xn}。若对所有的ω∈Ω,式子π(ω) > 0均成立,则称π为一个随机场。
当给每一个位置中按照某种分布随机赋予相空间的一个值之后,其全体就叫做随机场。我们不妨拿种地来打个比方。其中有两个概念:位置(site),相空间(phase space)。“位置”好比是一亩亩农田;“相空间”好比是种的各种庄稼。我们可以给不同的地种上不同的庄稼,这就好比给随机场的每个“位置”,赋予相空间里不同的值。所以,俗气点说,随机场就是在哪块地里种什么庄稼的事情。
-
团(Clique):图中节点的子集,其中任意两个节点之间都有边连接;
-
极大团:一个团,其中加入任何一个其他的节点都不能再形成团。
HammersleyClifford 定理:马尔可夫随机场中,多个变量之间的联合概率分布可以基于团分解为多个势函数的乘积,每个势函数仅与一个团相关。
5. 条件随机场 CRF
本节参考内容:如何用简单易懂的例子解释条件随机场(CRF)模型?、图模型(二)条件随机场(Conditional random field,CRF)、条件随机场 (CRF) 、CRF条件随机场的原理、例子、公式推导和应用。
条件随机场(conditional random field,CRF)是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型(即判别模型),其特点是假设输出随机变量构成马尔可夫随机场。
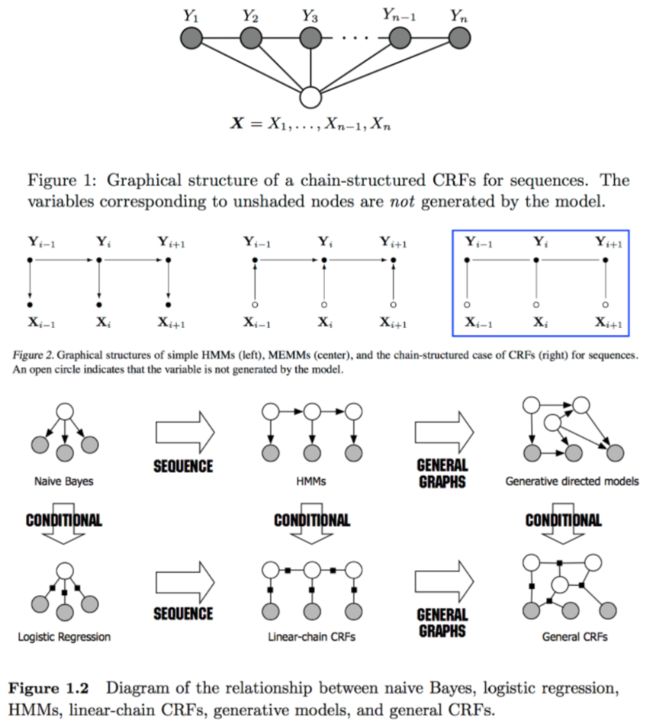
本节按照概率图、HMM、MEMM和CRF的顺序展开。
5.1 概率图
在统计概率图(probability graph models)中,参考宗成庆老师的书,是这样的体系结构:
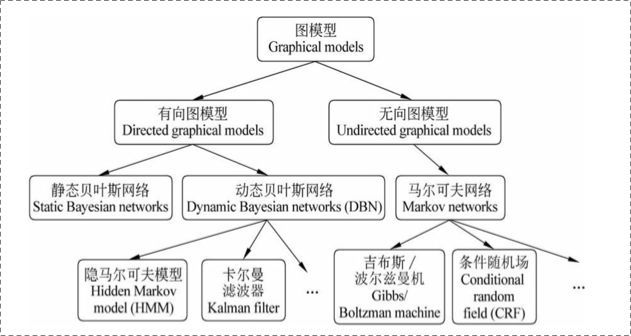
在概率图模型中,数据(样本)由公式 G = ( V , E ) G=(V,E) G=(V,E)建模表示:
- V V V表示节点,即随机变量(放在此处的,可以是一个token或者一个label),具体地,用 Y = ( y 1 , y 2 , … , y n ) Y = (y_1,y_2,…,y_n) Y=(y1,y2,…,yn)为随机变量建模,注意 Y Y Y现在是代表了一批随机变量(想象对应一条sequence,包含了很多的token), P ( Y ) P(Y) P(Y)为这些随机变量的分布;
- E E E表示边,即概率依赖关系。(具体结合后面的HMM或CRF的graph理解)
5.1.1 有向图与无向图
上图可以看到,贝叶斯网络(信念网络)都是有向的,马尔科夫网络无向。所以,贝叶斯网络适合为有单向依赖的数据建模,马尔科夫网络适合实体之间互相依赖的建模。
具体地,他们的核心差异表现在如何求 P = ( Y ) P=(Y) P=(Y),即怎么表示 Y = ( y 1 , y 2 , … , y n ) Y = (y_1,y_2,…,y_n) Y=(y1,y2,…,yn)这个的联合概率。
- 有向图:
对于有向图模型,这么求联合概率: P ( x 1 , x 2 , … , x n ) = ∏ i = 0 P ( x i ∣ π ( x i ) ) P(x_1,x_2,…,x_n)=∏_{i=0}P(x_i|\pi(x_i)) P(x1,x2,…,xn)=∏i=0P(xi∣π(xi))。
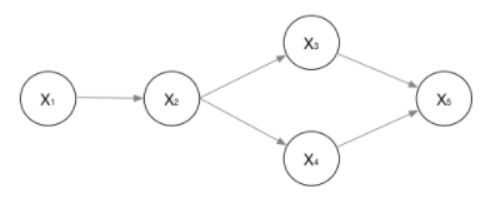
比如:对于下面的这个有向图(广义)的随机变量,应该这样表示他们的联合概率: P ( x 1 , … , x n ) = P ( x 1 ) ⋅ P ( x 2 ∣ x 1 ) ⋅ P ( x 3 ∣ x 2 ) ⋅ P ( x 4 ∣ x 2 ) ⋅ P ( x 5 ∣ x 3 , x 4 ) P(x_1,…,x_n) = P(x_1)·P(x_2|x_1)·P(x_3|x_2)·P(x_4|x_2)·P(x_5|x_3,x_4) P(x1,…,xn)=P(x1)⋅P(x2∣x1)⋅P(x3∣x2)⋅P(x4∣x2)⋅P(x5∣x3,x4)。
- 无向图:
对于无向图,一般就指马尔科夫网络,如下(广义):
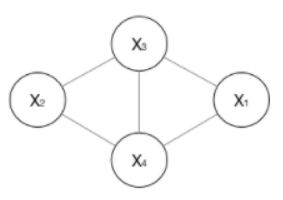
如果一个图太大,可以用因子分解将 P = ( Y ) P=(Y) P=(Y)写为若干个联合概率的乘积。怎么分解呢,将一个图分为若干个“小团”,注意每个团必须是“最大团”(里面任意两点连在了一块,比如上图的 X 1 , X 2 , X 3 X_1,X_2,X_3 X1,X2,X3是一个小团, X 2 , X 3 , X 4 X_2,X_3,X_4 X2,X3,X4是一个小团),则有:
P ( Y ) = ∏ c ψ c ( Y c ) Z ( x ) P(Y) = \frac{∏_cψ_c(Y_c)}{Z(x)} P(Y)=Z(x)∏cψc(Yc)
其中, Z ( x ) = ∑ Y ∏ c ψ c ( Y c ) Z(x) = \sum_Y∏_cψ_c(Y_c) Z(x)=∑Y∏cψc(Yc),应用这个归一化是为了让结果转换成概率。
因此,对于如上图所示的无向图,其概率为: P ( Y ) = ψ 1 ( X 1 , X 2 , X 3 ) ⋅ ψ 2 ( X 2 , X 3 , X 4 ) Z ( x ) P(Y) = \frac{ψ_1(X_1,X_2,X_3)·ψ_2(X_2,X_3,X_4)}{Z(x)} P(Y)=Z(x)ψ1(X1,X2,X3)⋅ψ2(X2,X3,X4)。其中, ψ c ( Y c ) ψ_c(Y_c) ψc(Yc)是一个最大团 C C C上所有随机变量的联合概率,一般取指数函数的势函数: ψ c ( Y c ) = e − E ( Y c ) = e ∑ k λ k f k ( c , y ∣ c , x ) ψ_c(Y_c)=e^{-E(Y_c)}=e^{\sum_kλ_kf_k(c,y|c,x)} ψc(Yc)=e−E(Yc)=e∑kλkfk(c,y∣c,x)。那么概率无向图的联合概率分布可以在因子分解下表示为:
P ( Y ) = ∏ c ψ c ( Y c ) Z ( x ) = ∏ c e ∑ k λ k f k ( c , y ∣ c , x ) Z ( x ) = e ∑ c ∑ k λ k f k ( y i , y i − 1 , x , i ) Z ( x ) P(Y) = \frac{∏_cψ_c(Y_c)}{Z(x)} = \frac{∏_ce^{\sum_kλ_kf_k(c,y|c,x)}}{Z(x)} = \frac{e^{\sum_c\sum_kλ_kf_k(y_i,y_{i-1},x,i)}}{Z(x)} P(Y)=Z(x)∏cψc(Yc)=Z(x)∏ce∑kλkfk(c,y∣c,x)=Z(x)e∑c∑kλkfk(yi,yi−1,x,i)
5.1.2 判别式(discriminative)模型vs生成式(generative)模型
在监督学习下,模型可以分为判别式模型与生成式模型。
5.2 序列建模
常见的序列有如:时序数据、本文句子、语音数据、等等。广义下的序列有这些特点:
- 节点之间有关联依赖性/无关联依赖性
- 序列的节点是随机的/确定的
- 序列是线性变化/非线性的
对不同的序列有不同的问题需求,常见的序列建模方法总结有如下:
- 拟合,预测未来节点(或走势分析):
- 常规序列建模方法:AR、MA、ARMA、ARIMA
- 回归拟合
- Neural Networks
- 判断不同序列类别,分类问题:
- HMM、CRF、General Classifier(ML models、NN models)
- 不同时序对应的状态的分析,序列标注问题:
- HMM、CRF、RecurrentNNs
5.3 CRF的定义与形式
啊 整理不下去了,之后的话可以感觉看看这几篇文章:图模型(二)条件随机场、机器学习-条件随机场、统计机器学习-条件随机场、条件随机场。后续应该是到需要具体做命名实体识别的时候才会再过来看吧。对没有开过线代、统计、概率论的课(只上过高数四),纯粹靠自学的人来说,太不友好了,给爷累死了 555。
条件随机场(Conditional random field,CRF)是条件概率分布模型 P(Y|X) ,表示的是给定一组输入随机变量 X 的条件下另一组输出随机变量 Y 的马尔可夫随机场,也就是说 CRF 的特点是假设输出随机变量构成马尔可夫随机场。条件随机场可被看作是最大熵马尔可夫模型在标注问题上的推广。
大部分介绍的都是用于序列标注问题的线性链条件随机场(linear chain conditional CRF),是由输入序列来预测输出序列的判别式模型。
从问题描述上看,对于序列标注问题,X 是需要标注的观测序列,Y 是标记序列(状态序列)。在学习过程时,通过 MLE 或带正则的 MLE 来训练出模型参数;在测试过程,对于给定的观测序列,模型需要求出条件概率最大的输出序列。
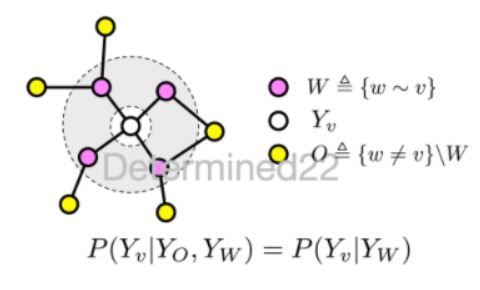
如果随机变量 Y 构成一个由无向图 G=(V, E) 表示的马尔可夫随机场,对任意节点 v∈V都成立,即 P ( Y v ∣ X , Y w , w ≠ v ) = P ( Y v ∣ X , Y w , w ∼ v ) P(Y_v|X,Y_w,w≠v)=P(Y_v|X,Y_w,w∼v) P(Yv∣X,Yw,w=v)=P(Yv∣X,Yw,w∼v)对任意节点v 都成立,则称 P(Y|X) 是条件随机场。式中w≠v表示 w 是除v以外的所有节点,w∼v表示 w 是与 v 相连接的所有节点。不妨把等式两边的相同的条件 X 都遮住,那么式子可以用下图示意:
这就是马尔可夫随机场的定义。
线性链条件随机场: 在定义中并没有要求 X 和 Y 具有相同的结构,而在现实中,一般假设 X 和 Y 有相同的图结构。对于线性链条件随机场来说,图 G 的每条边都存在于状态序列 Y 的相邻两个节点,最大团 C 是相邻两个节点的集合,X 和 Y 有相同的图结构意味着每个 Xi都与 Yi一一对应。
V = 1 , 2 , . . . , n , E = ( i , i + 1 ) , i = 1 , 2 , . . . , n − 1 V = 1 , 2 , . . . , n , E = ( i , i + 1 ) , i = 1 , 2 , . . . , n − 1 V={1,2,...,n},E={(i,i+1)},i=1,2,...,n−1V={1,2,...,n},E={(i,i+1)},i=1,2,...,n−1 V=1,2,...,n,E=(i,i+1),i=1,2,...,n−1V=1,2,...,n,E=(i,i+1),i=1,2,...,n−1
设两组随机变量 X = ( X 1 , . . . , X n ) , Y = ( Y 1 , . . . , Y n ) X=(X1,...,Xn),Y=(Y1,...,Yn) X=(X1,...,Xn),Y=(Y1,...,Yn),那么线性链条件随机场的定义为(其中当 i 取 1 或 n 时只考虑单边):
P ( Y i ∣ X , Y 1 , . . . , Y i − 1 , Y i + 1 , . . . , Y n ) = P ( Y i ∣ X , Y i − 1 , Y i + 1 ) , i = 1 , . . . , n P(Yi|X,Y1,...,Yi−1,Yi+1,...,Yn)=P(Yi|X,Yi−1,Yi+1),i=1,...,n P(Yi∣X,Y1,...,Yi−1,Yi+1,...,Yn)=P(Yi∣X,Yi−1,Yi+1),i=1,...,n