转载
Python之matplotlib基础
matplotlib是Python优秀的数据可视化第三方库
matplotlib库的效果可参考
http://matplotlib.org/gallery.html
matplotlib的使用 由各种可视化类构成,内部结构复杂,受matlab库启发,matplotlab.pyplot是绘制种类可视化图形的命令子库,相当于快捷方式
import matplotlib.pyplot as plt
一个小示例
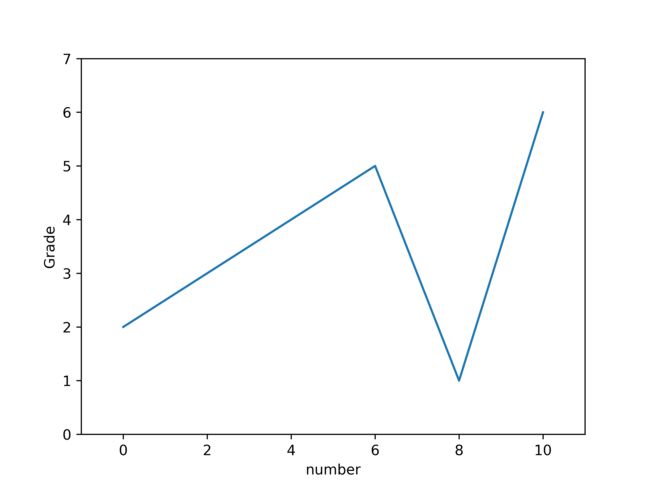
import matplotlib.pyplot as plt plt.plot([2,3,4,5,1,6]) plt.ylabel("Grade") plt.ylabel("number") plt.axis([-1,11,0,7]) plt.savefig('test',dpi=600)#plt.savefig()将输出图形存储为文件,默认为png格式,可以通过dpi修改输出质量 plt.show()绘制多图subplot
plot.subplot(nrows,ncols,plot_number)
在全局绘制区域中创建一个分区体系,并定位到一个子绘图区域
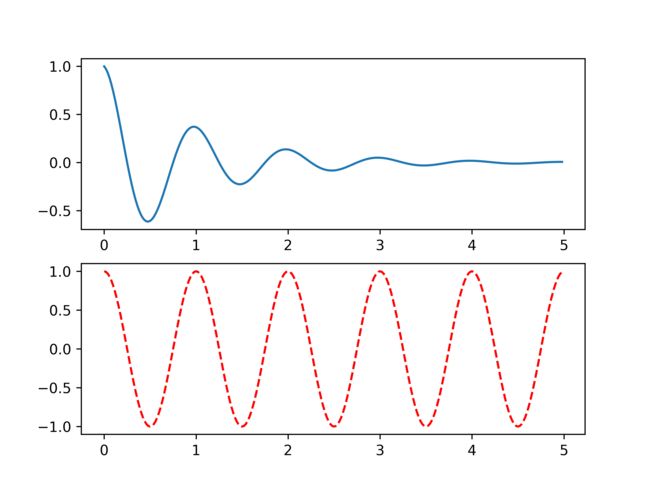
pyplot绘图区域示例
import numpy as np import matplotlib.pyplot as plt def f(t): return np.exp(-t) * np.cos(2 * np.pi * t) a = np.arange(0.0, 5.0, 0.02) plt.subplot(211) plt.plot(a, f(a)) plt.subplot(2, 1, 2) plt.plot(a, np.cos(2 * np.pi * a), 'r--') plt.savefig('test',dpi=600) plt.show()pyplot的plot()函数详解
plt.plot(x,y,format_string,**kwargs)
x:x轴数据,列表或数组,可选
y:y轴数据,列表或数组
format_string: 控制曲线的格式字符串,可迁
**kwargs: 第二组或更多的(x,y,format_string)注意:当绘制多条曲线时,各条曲线的x不能省略
format_string:控制曲线的格式字符串,可选。由颜色字符、风格字符和标记字符组成
| 颜色字符 | 说明 | 颜色字符 | 说明 |
|---|---|---|---|
| 'b' | blue | 'm' | magenta洋红色 |
| 'g' | green | 'y' | 黄色 |
| 'r' | red | 'k' | 黑色 |
| 'c' | cyan青绿色 | 'w' | 白色 |
| '#008000' | RGB某颜色 | '0.8' | 灰度值字符串 |
| 风格字符 | 说明 |
|---|---|
| '-' | 实线 |
| '--' | 破折线 |
| '-.' | 点划线 |
| ':' | 虚线 |
| ' ' | 无线条 |
| 标记字符 | 说明 | 标记字符 | 说明 | 标记字符 | 说明 |
|---|---|---|---|---|---|
| '.' | 点标记 | '1' | 下花三角标记 | 'h' | 竖六边形标记 |
| ',' | 像素标记(极小点) | '2' | 上花三角标记 | 'H' | 横六边形标记 |
| 'o' | 实心圏标记 | '3' | 左花三角标记 | '+' | 十字形标记 |
| 'v' | 倒三角标记 | '4' | 右花三角标记 | 'x' | x标记 |
| '^' | 上三角标记 | 's' | 实心方形标记 | 'D' | 菱形标记 |
| '>' | 右三角标记 | 'p' | 实心五角标记 | 'd' | 瘦菱形标记 |
| '<' | 左三角标记 | '*' | 星形标记 | ' | ' |
**kwargs: 第二组或更多(x,y,format_string)
color: 控制颜色 如color='green'
linestyle:线条控制 如linestyle='dashed' marker:标记风格,marker='o' markerfacecolor:标记颜色,markerfacecolor='blue' markersize:标记尺寸,markersize=20 ...pyplot的中文显示
pyplot并不默认支持中文显示,需要rcParams修改字体实现
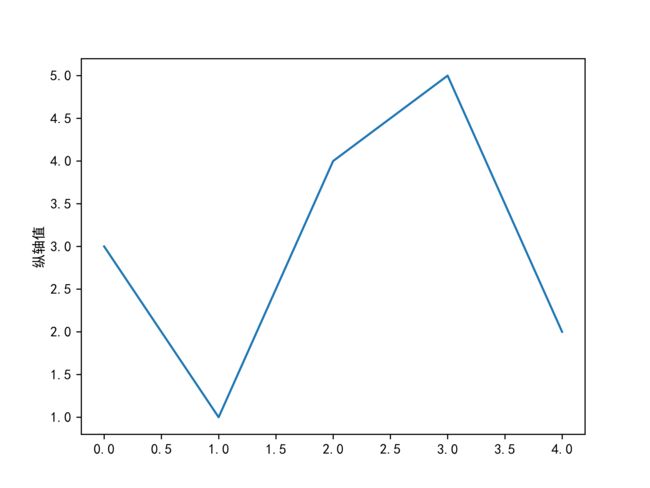
全局设置中文字体
import matplotlib
import matplotlib.pyplot as plt matplotlib.rcParams['font.family']='SimHei' plt.plot([3,1,4,5,2]) plt.ylabel('纵轴值') plt.savefig('test',dpi=600) plt.show()rcParams的属性
| 属性 | 说明 |
|---|---|
| 'font.family' | 用于显示字体的名字 |
| 'font.style' | 字体风格,正常'normal'或斜体'italic' |
| 'font.size' | 字体大小,整数字号或者'large','x-small' |
中文字体的种类
rcParams['font.family']
| 中文字体 | 说明 |
|------------|----------|
| 'SimHei' | 中文黑体 |
| 'Kaiti' | 中文楷体 |
| 'LiSu' | 中文隶书 |
| 'FangSong' | 中文仿宋 |
| 'YouYuan' | 中文幼圆 |
| STSong | 华文宋体 |
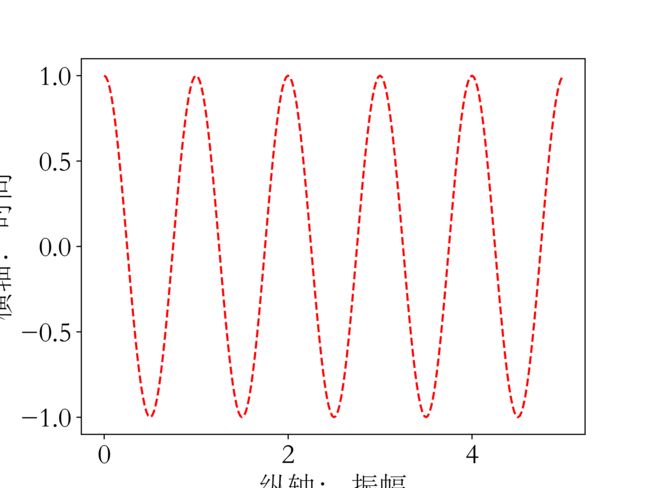
示例:
import matplotlib
import matplotlib.pyplot as plt import numpy as np matplotlib.rcParams['font.family']='STSong' matplotlib.rcParams['font.size']=20 a = np.arange(0.0,5.0,0.02) plt.xlabel('纵轴: 振幅') plt.ylabel('横轴: 时间') plt.plot(a,np.cos(2*np.pi*a),'r--') plt.savefig('test',dpi=600) plt.show()局部设置中文字体
在有中文输出的地方,增加一个属性:fontproperties
import matplotlib.pyplot as plt import numpy as np a = np.arange(0.0,5.0,0.02) plt.xlabel('纵轴: 振幅', fontproperties='SimHei',fontsize=20) plt.ylabel('横轴: 时间', fontproperties='SimHei',fontsize=20) plt.plot(a,np.cos(2*np.pi*a),'r--') plt.savefig('test',dpi=600) plt.show()
注意到,如果设置全局字体的话,那么坐标轴的字体也被改变,局部设置中文字体不改变坐标轴的字体。
pyplot的文本显示
pyplot的文本显示函数
| 函数 | 说明 |
|----------------|--------------------------|
| plt.xlabel() | 对x轴增加文本标签 |
| plt.ylabel() | 对y轴增加文本标签 |
| plt.title() | 对图形本整体增加文本标签 |
| plt.text() | 在任意位置增加文本 |
| plt.annotate() | 在图形中增加带箭头的注释 |
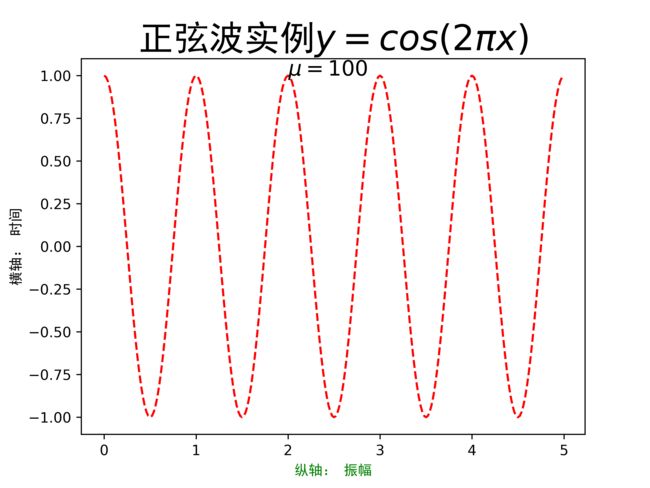
text函数示例
import matplotlib.pyplot as plt import numpy as np a = np.arange(0.0,5.0,0.02) plt.xlabel('纵轴: 振幅', fontproperties='SimHei', fontsize=20, color = 'green') plt.ylabel('横轴: 时间', fontproperties='SimHei', fontsize=20) plt.title(r'正弦波实例$y=cos(2\pi x)$',fontproperties='SimHei',fontsize=25) plt.text(2,1,r'$\mu=100$',fontsize=15) plt.plot(a,np.cos(2*np.pi*a),'r--') plt.savefig('test',dpi=600) plt.show()annotate函数示例
import matplotlib.pyplot as plt import numpy as np a = np.arange(0.0,5.0,0.02) plt.plot(a,np.cos(2*np.pi*a),'r--') plt.xlabel('纵轴: 振幅', fontproperties='SimHei', fontsize=20, color = 'green') plt.ylabel('横轴: 时间', fontproperties='SimHei', fontsize=20) plt.title(r'正弦波实例$y=cos(2\pi x)$',fontproperties='SimHei',fontsize=25) plt.annotate(r'$\mu=100$',xy=(2,1),xytext=(3,1.5), arrowprops=dict(facecolor='black',shrink=0.1,width=2)) plt.axis([-1,6,-2,2]) plt.grid() plt.savefig('test',dpi=600) plt.show()
介绍
Matplotlib 可能是 Python 2D-绘图领域使用最广泛的套件。它能让使用者很轻松地将数据图形化,并且提供多样化的输出格式。这里将会探索 matplotlib 的常见用法。
IPython 以及 pylab 模式
IPython 是 Python 的一个增强版本。它在下列方面有所增强:命名输入输出、使用系统命令(shell commands)、排错(debug)能力。我们在命令行终端给 IPython 加上参数 -pylab (0.12 以后的版本是 --pylab)之后,就可以像 Matlab 或者 Mathematica 那样以交互的方式绘图。
pylab
pylab 是 matplotlib 面向对象绘图库的一个接口。它的语法和 Matlab 十分相近。也就是说,它主要的绘图命令和 Matlab 对应的命令有相似的参数。
初级绘制
这一节中,我们将从简到繁:先尝试用默认配置在同一张图上绘制正弦和余弦函数图像,然后逐步美化它。
第一步,是取得正弦函数和预先函数的值:
1
2
3
4
|
from pylab import *
X = np.linspace(-np.pi, np.pi, 256,endpoint=True) C,S = np.cos(X), np.sin(X) |
X 是一个 numpy 数组,包含了从 到 等间隔的 256 个值。C 和 S 则分别是这 256 个值对应的余弦和正弦函数值组成的numpy 数组。
你可以在 IPython 的交互模式下测试代码,也可以下载代码(下载链接就是这些示例图),然后执行:
1
|
python exercise_1.py
|
使用默认配置
Matplotlib 的默认配置都允许用户自定义。你可以调整大多数的默认配置:图片大小和分辨率(dpi)、线宽、颜色、风格、坐标轴、坐标轴以及网格的属性、文字与字体属性等。不过,matplotlib 的默认配置在大多数情况下已经做得足够好,你可能只在很少的情况下才会想更改这些默认配置。
1
2
3
4
5
6 7 8 9 |
from pylab import *
X = np.linspace(-np.pi, np.pi, 256,endpoint=True) C,S = np.cos(X), np.sin(X) plot(X,C) plot(X,S) show() |
默认配置的具体内容
下面的代码中,我们展现了 matplotlib 的默认配置并辅以注释说明,这部分配置包含了有关绘图样式的所有配置。代码中的配置与默认配置完全相同,你可以在交互模式中修改其中的值来观察效果。
1
2
3
4
5
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# 导入 matplotlib 的所有内容(nympy 可以用 np 这个名字来使用)
from pylab import *
# 创建一个 8 * 6 点(point)的图,并设置分辨率为 80 figure(figsize=(8,6), dpi=80) # 创建一个新的 1 * 1 的子图,接下来的图样绘制在其中的第 1 块(也是唯一的一块) subplot(1,1,1) X = np.linspace(-np.pi, np.pi, 256,endpoint=True) C,S = np.cos(X), np.sin(X) # 绘制余弦曲线,使用蓝色的、连续的、宽度为 1 (像素)的线条 plot(X, C, color="blue", linewidth=1.0, linestyle="-") # 绘制正弦曲线,使用绿色的、连续的、宽度为 1 (像素)的线条 plot(X, S, color="green", linewidth=1.0, linestyle="-") # 设置横轴的上下限 xlim(-4.0,4.0) # 设置横轴记号 xticks(np.linspace(-4,4,9,endpoint=True)) # 设置纵轴的上下限 ylim(-1.0,1.0) # 设置纵轴记号 yticks(np.linspace(-1,1,5,endpoint=True)) # 以分辨率 72 来保存图片 # savefig("exercice_2.png",dpi=72) # 在屏幕上显示 show() |
改变线条的颜色和粗细
首先,我们以蓝色和红色分别表示余弦和正弦函数,而后将线条变粗一点。接下来,我们在水平方向拉伸一下整个图。
1
2
3
4
5
|
...
figure(figsize=(10,6), dpi=80)
plot(X, C, color="blue", linewidth=2.5, linestyle="-") plot(X, S, color="red", linewidth=2.5, linestyle="-") ... |
设置图片边界
当前的图片边界设置得不好,所以有些地方看得不是很清楚。
1
2
3
4
|
...
xlim(X.min()*1.1, X.max()*1.1)
ylim(C.min()*1.1, C.max()*1.1) ... |
更好的方式是这样:
1
2
3
4
5
6 7 8 |
xmin ,xmax = X.min(), X.max()
ymin, ymax = Y.min(), Y.max()
dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2 xlim(xmin - dx, xmax + dx) ylim(ymin - dy, ymax + dy) |
设置记号
我们讨论正弦和余弦函数的时候,通常希望知道函数在 和 的值。这样看来,当前的设置就不那么理想了。
1
2
3
4
|
...
xticks( [-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
yticks([-1, 0, +1]) ... |
设置记号的标签
记号现在没问题了,不过标签却不大符合期望。我们可以把 当做是 ,但毕竟不够精确。当我们设置记号的时候,我们可以同时设置记号的标签。注意这里使用了 LaTeX。
1
2
3
4
5
6 7 |
...
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
[r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$']) yticks([-1, 0, +1], [r'$-1$', r'$0$', r'$+1$']) ... |
移动脊柱
坐标轴线和上面的记号连在一起就形成了脊柱(Spines,一条线段上有一系列的凸起,是不是很像脊柱骨啊~),它记录了数据区域的范围。它们可以放在任意位置,不过至今为止,我们都把它放在图的四边。
实际上每幅图有四条脊柱(上下左右),为了将脊柱放在图的中间,我们必须将其中的两条(上和右)设置为无色,然后调整剩下的两条到合适的位置——数据空间的 0 点。
1
2
3
4
5
6 7 8 9 |
...
ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none') ax.xaxis.set_ticks_position('bottom') ax.spines['bottom'].set_position(('data',0)) ax.yaxis.set_ticks_position('left') ax.spines['left'].set_position(('data',0)) ... |
添加图例
我们在图的左上角添加一个图例。为此,我们只需要在 plot 函数里以「键 - 值」的形式增加一个参数。
1
2
3
4
5
6 |
...
plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine") plot(X, S, color="red", linewidth=2.5, linestyle="-", label="sine") legend(loc='upper left') ... |
给一些特殊点做注释
我们希望在 的位置给两条函数曲线加上一个注释。首先,我们在对应的函数图像位置上画一个点;然后,向横轴引一条垂线,以虚线标记;最后,写上标签。
1
2
3
4
5
6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
...
t = 2*np.pi/3
plot([t,t],[0,np.cos(t)], color ='blue', linewidth=2.5, linestyle="--") scatter([t,],[np.cos(t),], 50, color ='blue') annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$', xy=(t, np.sin(t)), xycoords='data', xytext=(+10, +30), textcoords='offset points', fontsize=16, arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) plot([t,t],[0,np.sin(t)], color ='red', linewidth=2.5, linestyle="--") scatter([t,],[np.sin(t),], 50, color ='red') annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$', xy=(t, np.cos(t)), xycoords='data', xytext=(-90, -50), textcoords='offset points', fontsize=16, arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) ... |
精益求精
坐标轴上的记号标签被曲线挡住了,作为强迫症患者(雾)这是不能忍的。我们可以把它们放大,然后添加一个白色的半透明底色。这样可以保证标签和曲线同时可见。
1
2
3
4
5
|
...
for label in ax.get_xticklabels() + ax.get_yticklabels():
label.set_fontsize(16) label.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.65 )) ... |
图像、子图、坐标轴和记号
到目前为止,我们都用隐式的方法来绘制图像和坐标轴。快速绘图中,这是很方便的。我们也可以显式地控制图像、子图、坐标轴。Matplotlib 中的「图像」指的是用户界面看到的整个窗口内容。在图像里面有所谓「子图」。子图的位置是由坐标网格确定的,而「坐标轴」却不受此限制,可以放在图像的任意位置。我们已经隐式地使用过图像和子图:当我们调用 plot 函数的时候,matplotlib 调用 gca() 函数以及 gcf() 函数来获取当前的坐标轴和图像;如果无法获取图像,则会调用 figure() 函数来创建一个——严格地说,是用 subplot(1,1,1) 创建一个只有一个子图的图像。
图像
所谓「图像」就是 GUI 里以「Figure #」为标题的那些窗口。图像编号从 1 开始,与 MATLAB 的风格一致,而于 Python 从 0 开始编号的风格不同。以下参数是图像的属性:
| 参数 | 默认值 | 描述 |
|---|---|---|
| num | 1 | 图像的数量 |
| figsize | figure.figsize | 图像的长和宽(英寸) |
| dpi | figure.dpi | 分辨率(点/英寸) |
| facecolor | figure.facecolor | 绘图区域的背景颜色 |
| edgecolor | figure.edgecolor | 绘图区域边缘的颜色 |
| frameon | True | 是否绘制图像边缘 |
这些默认值可以在源文件中指明。不过除了图像数量这个参数,其余的参数都很少修改。
你在图形界面中可以按下右上角的 X 来关闭窗口(OS X 系统是左上角)。Matplotlib 也提供了名为 close 的函数来关闭这个窗口。close 函数的具体行为取决于你提供的参数:
- 不传递参数:关闭当前窗口;
- 传递窗口编号或窗口实例(instance)作为参数:关闭指定的窗口;
all:关闭所有窗口。
和其他对象一样,你可以使用 setp 或者是 set_something 这样的方法来设置图像的属性。
子图
你可以用子图来将图样(plot)放在均匀的坐标网格中。用 subplot 函数的时候,你需要指明网格的行列数量,以及你希望将图样放在哪一个网格区域中。此外,gridspec 的功能更强大,你也可以选择它来实现这个功能。
坐标轴
坐标轴和子图功能类似,不过它可以放在图像的任意位置。因此,如果你希望在一副图中绘制一个小图,就可以用这个功能。
记号
良好的记号是图像的重要组成部分。Matplotlib 里的记号系统里的各个细节都是可以由用户个性化配置的。你可以用 Tick Locators 来指定在那些位置放置记号,用 Tick Formatters 来调整记号的样式。主要和次要的记号可以以不同的方式呈现。默认情况下,每一个次要的记号都是隐藏的,也就是说,默认情况下的次要记号列表是空的——NullLocator。
Tick Locators
下面有为不同需求设计的一些 Locators。
| 类型 | 说明 |
|---|---|
| NullLocator | No ticks. |
| IndexLocator | Place a tick on every multiple of some base number of points plotted. |
| FixedLocator | Tick locations are fixed. |
| LinearLocator | Determine the tick locations. |
| MultipleLocator | Set a tick on every integer that is multiple of some base. |
| AutoLocator | Select no more than n intervals at nice locations. |
| LogLocator | Determine the tick locations for log axes. |
这些 Locators 都是 matplotlib.ticker.Locator 的子类,你可以据此定义自己的 Locator。以日期为 ticks 特别复杂,因此 Matplotlib 提供了 matplotlib.dates 来实现这一功能。
其他类型的图
接下来的内容是练习。请运用你学到的知识,从提供的代码开始,实现配图所示的效果。具体的答案可以点击配图下载。
普通图
1
2
3
4
5
6 7 8 9 |
from pylab import *
n = 256 X = np.linspace(-np.pi,np.pi,n,endpoint=True) Y = np.sin(2*X) plot (X, Y+1, color='blue', alpha=1.00) plot (X, Y-1, color='blue', alpha=1.00) show() |
散点图
1
2
3
4
5
6 7 8 |
from pylab import *
n = 1024 X = np.random.normal(0,1,n) Y = np.random.normal(0,1,n) scatter(X,Y) show() |
条形图
1
2
3
4
5
6 7 8 9 10 11 12 13 14 15 |
from pylab import *
n = 12 X = np.arange(n) Y1 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n) Y2 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n) bar(X, +Y1, facecolor='#9999ff', edgecolor='white') bar(X, -Y2, facecolor='#ff9999', edgecolor='white') for x,y in zip(X,Y1): text(x+0.4, y+0.05, '%.2f' % y, ha='center', va= 'bottom') ylim(-1.25,+1.25) show() |
等高线图
1
2
3
4
5
6 7 8 9 10 11 12 |
from pylab import *
def f(x,y): return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2) n = 256 x = np.linspace(-3,3,n) y = np.linspace(-3,3,n) X,Y = np.meshgrid(x,y) contourf(X, Y, f(X,Y), 8, alpha=.75, cmap='jet') C = contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5) show() |
灰度图(Imshow)
1
2
3
4
5
6 7 8 9 |
from pylab import *
def f(x,y): return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2) n = 10 x = np.linspace(-3,3,4*n) y = np.linspace(-3,3,3*n) X,Y = np.meshgrid(x,y) imshow(f(X,Y)), show() |
饼状图
1
2
3
4
5
|
from pylab import *
n = 20 Z = np.random.uniform(0,1,n) pie(Z), show() |
量场图(Quiver Plots)
1
2
3
4
5
|
from pylab import *
n = 8 X,Y = np.mgrid[0:n,0:n] quiver(X,Y), show() |
网格
1
2
3
4
5
6 7 8 9 |
from pylab import *
axes = gca()
axes.set_xlim(0,4) axes.set_ylim(0,3) axes.set_xticklabels([]) axes.set_yticklabels([]) show() |
多重网格
1
2
3
4
5
6 7 |
from pylab import *
subplot(2,2,1) subplot(2,2,3) subplot(2,2,4) show() |
极轴图
1
2
3
4
5
6 7 8 9 10 11 12 13 14 15 |
from pylab import *
axes([0,0,1,1]) N = 20 theta = np.arange(0.0, 2*np.pi, 2*np.pi/N) radii = 10*np.random.rand(N) width = np.pi/4*np.random.rand(N) bars = bar(theta, radii, width=width, bottom=0.0) for r,bar in zip(radii, bars): bar.set_facecolor( cm.jet(r/10.)) bar.set_alpha(0.5) show() |
3D 图
1
2
3
4
5
6 7 8 9 10 11 12 13 14 |
from pylab import *
from mpl_toolkits.mplot3d import Axes3D fig = figure() ax = Axes3D(fig) X = np.arange(-4, 4, 0.25) Y = np.arange(-4, 4, 0.25) X, Y = np.meshgrid(X, Y) R = np.sqrt(X**2 + Y**2) Z = np.sin(R) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='hot') show() |
手稿
Python的可视化包 – Matplotlib
Matplotlib是Python中最常用的可视化工具之一,可以非常方便地创建海量类型地2D图表和一些基本的3D图表。Matplotlib最早是为了可视化癫痫病人的脑皮层电图相关的信号而研发,因为在函数的设计上参考了MATLAB,所以叫做Matplotlib。Matplotlib首次发表于2007年,在开源和社区的推动下,现在在基于Python的各个科学计算领域都得到了广泛应用。Matplotlib的原作者John D. Hunter博士是一名神经生物学家,2012年不幸因癌症去世,感谢他创建了这样一个伟大的库。
安装Matplotlib的方式和numpy很像,可以直接通过Unix/Linux的软件管理工具,比如Ubuntu 16.04 LTS下,输入:
>> sudo apt install python-matplotlib
或者通过pip安装:
>> pip install matplotlib
Windows下也可以通过pip,或是到官网下载:
python plotting – Matplotlib 1.5.3 documentation
Matplotlib非常强大,不过在深度学习中常用的其实只有很基础的一些功能,这节主要介绍2D图表,3D图表和图像显示。
5.4.1 2D图表
Matplotlib中最基础的模块是pyplot。先从最简单的点图和线图开始,比如我们有一组数据,还有一个拟合模型,通过下面的代码图来可视化:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# 通过rcParams设置全局横纵轴字体大小
mpl.rcParams['xtick.labelsize'] = 24
mpl.rcParams['ytick.labelsize'] = 24
np.random.seed(42)
# x轴的采样点
x = np.linspace(0, 5, 100)
# 通过下面曲线加上噪声生成数据,所以拟合模型就用y了……
y = 2*np.sin(x) + 0.3*x**2
y_data = y + np.random.normal(scale=0.3, size=100)
# figure()指定图表名称
plt.figure('data')
# '.'标明画散点图,每个散点的形状是个圆
plt.plot(x, y_data, '.')
# 画模型的图,plot函数默认画连线图
plt.figure('model')
plt.plot(x, y)
# 两个图画一起
plt.figure('data & model')
# 通过'k'指定线的颜色,lw指定线的宽度
# 第三个参数除了颜色也可以指定线形,比如'r--'表示红色虚线
# 更多属性可以参考官网:http://matplotlib.org/api/pyplot_api.html
plt.plot(x, y, 'k', lw=3)
# scatter可以更容易地生成散点图
plt.scatter(x, y_data)
# 将当前figure的图保存到文件result.png
plt.savefig('result.png')
# 一定要加上这句才能让画好的图显示在屏幕上
plt.show()
|
matplotlib和pyplot的惯用别名分别是mpl和plt,上面代码生成的图像如下:
![]()
![]()
![]()
基本的画图方法就是这么简单,如果想了解更多pyplot的属性和方法来画出风格多样的图像,可以参考官网:
pyplot – Matplotlib 1.5.3 documentation
Customizing matplotlib
点和线图表只是最基本的用法,有的时候我们获取了分组数据要做对比,柱状或饼状类型的图或许更合适:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['axes.titlesize'] = 20
mpl.rcParams['xtick.labelsize'] = 16
mpl.rcParams['ytick.labelsize'] = 16
mpl.rcParams['axes.labelsize'] = 16
mpl.rcParams['xtick.major.size'] = 0
mpl.rcParams['ytick.major.size'] = 0
# 包含了狗,猫和猎豹的最高奔跑速度,还有对应的可视化颜色
speed_map = {
'dog': (48, '#7199cf'),
'cat': (45, '#4fc4aa'),
'cheetah': (120, '#e1a7a2')
}
# 整体图的标题
fig = plt.figure('Bar chart & Pie chart')
# 在整张图上加入一个子图,121的意思是在一个1行2列的子图中的第一张
ax = fig.add_subplot(121)
ax.set_title('Running speed - bar chart')
# 生成x轴每个元素的位置
xticks = np.arange(3)
# 定义柱状图每个柱的宽度
bar_width = 0.5
# 动物名称
animals = speed_map.keys()
# 奔跑速度
speeds = [x[0] for x in speed_map.values()]
# 对应颜色
colors = [x[1] for x in speed_map.values()]
# 画柱状图,横轴是动物标签的位置,纵轴是速度,定义柱的宽度,同时设置柱的边缘为透明
bars = ax.bar(xticks, speeds, width=bar_width, edgecolor='none')
# 设置y轴的标题
ax.set_ylabel('Speed(km/h)')
# x轴每个标签的具体位置,设置为每个柱的中央
ax.set_xticks(xticks+bar_width/2)
# 设置每个标签的名字
ax.set_xticklabels(animals)
# 设置x轴的范围
ax.set_xlim([bar_width/2-0.5, 3-bar_width/2])
# 设置y轴的范围
ax.set_ylim([0, 125])
# 给每个bar分配指定的颜色
for bar, color in zip(bars, colors):
bar.set_color(color)
# 在122位置加入新的图
ax = fig.add_subplot(122)
ax.set_title('Running speed - pie chart')
# 生成同时包含名称和速度的标签
labels = ['{}\n{} km/h'.format(animal, speed) for animal, speed in zip(animals, speeds)]
# 画饼状图,并指定标签和对应颜色
ax.pie(speeds, labels=labels, colors=colors)
plt.show()
|
在这段代码中又出现了一个新的东西叫做,一个用ax命名的对象。在Matplotlib中,画图时有两个常用概念,一个是平时画图蹦出的一个窗口,这叫一个figure。Figure相当于一个大的画布,在每个figure中,又可以存在多个子图,这种子图叫做axes。顾名思义,有了横纵轴就是一幅简单的图表。在上面代码中,先把figure定义成了一个一行两列的大画布,然后通过fig.add_subplot()加入两个新的子图。subplot的定义格式很有趣,数字的前两位分别定义行数和列数,最后一位定义新加入子图的所处顺序,当然想写明确些也没问题,用逗号分开即可。。上面这段代码产生的图像如下:
![]()
5.3.1 3D图表
Matplotlib中也能支持一些基础的3D图表,比如曲面图,散点图和柱状图。这些3D图表需要使用mpl_toolkits模块,先来看一个简单的曲面图的例子:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
import matplotlib.pyplot as plt
import numpy as np
# 3D图标必须的模块,project='3d'的定义
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(42)
n_grids = 51 # x-y平面的格点数
c = n_grids / 2 # 中心位置
nf = 2 # 低频成分的个数
# 生成格点
x = np.linspace(0, 1, n_grids)
y = np.linspace(0, 1, n_grids)
# x和y是长度为n_grids的array
# meshgrid会把x和y组合成n_grids*n_grids的array,X和Y对应位置就是所有格点的坐标
X, Y = np.meshgrid(x, y)
# 生成一个0值的傅里叶谱
spectrum = np.zeros((n_grids, n_grids), dtype=np.complex)
# 生成一段噪音,长度是(2*nf+1)**2/2
noise = [np.complex(x, y) for x, y in np.random.uniform(-1,1,((2*nf+1)**2/2, 2))]
# 傅里叶频谱的每一项和其共轭关于中心对称
noisy_block = np.concatenate((noise, [0j], np.conjugate(noise[::-1])))
# 将生成的频谱作为低频成分
spectrum[c-nf:c+nf+1, c-nf:c+nf+1] = noisy_block.reshape((2*nf+1, 2*nf+1))
# 进行反傅里叶变换
Z = np.real(np.fft.ifft2(np.fft.ifftshift(spectrum)))
# 创建图表
fig = plt.figure('3D surface & wire')
# 第一个子图,surface图
ax = fig.add_subplot(1, 2, 1, projection='3d')
# alpha定义透明度,cmap是color map
# rstride和cstride是两个方向上的采样,越小越精细,lw是线宽
ax.plot_surface(X, Y, Z, alpha=0.7, cmap='jet', rstride=1, cstride=1, lw=0)
# 第二个子图,网线图
ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_wireframe(X, Y, Z, rstride=3, cstride=3, lw=0.5)
plt.show()
|
这个例子中先生成一个所有值均为0的复数array作为初始频谱,然后把频谱中央部分用随机生成,但同时共轭关于中心对称的子矩阵进行填充。这相当于只有低频成分的一个随机频谱。最后进行反傅里叶变换就得到一个随机波动的曲面,图像如下:
![]()
3D的散点图也是常常用来查看空间样本分布的一种手段,并且画起来比表面图和网线图更加简单,来看例子:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(42)
# 采样个数500
n_samples = 500
dim = 3
# 先生成一组3维正态分布数据,数据方向完全随机
samples = np.random.multivariate_normal(
np.zeros(dim),
np.eye(dim),
n_samples
)
# 通过把每个样本到原点距离和均匀分布吻合得到球体内均匀分布的样本
for i in range(samples.shape[0]):
r = np.power(np.random.random(), 1.0/3.0)
samples[i] *= r / np.linalg.norm(samples[i])
upper_samples = []
lower_samples = []
for x, y, z in samples:
# 3x+2y-z=1作为判别平面
if z > 3*x + 2*y - 1:
upper_samples.append((x, y, z))
else:
lower_samples.append((x, y, z))
fig = plt.figure('3D scatter plot')
ax = fig.add_subplot(111, projection='3d')
uppers = np.array(upper_samples)
lowers = np.array(lower_samples)
# 用不同颜色不同形状的图标表示平面上下的样本
# 判别平面上半部分为红色圆点,下半部分为绿色三角
ax.scatter(uppers[:, 0], uppers[:, 1], uppers[:, 2], c='r', marker='o')
ax.scatter(lowers[:, 0], lowers[:, 1], lowers[:, 2], c='g', marker='^')
plt.show()
|
这个例子中,为了方便,直接先采样了一堆3维的正态分布样本,保证方向上的均匀性。然后归一化,让每个样本到原点的距离为1,相当于得到了一个均匀分布在球面上的样本。再接着把每个样本都乘上一个均匀分布随机数的开3次方,这样就得到了在球体内均匀分布的样本,最后根据判别平面3x+2y-z-1=0对平面两侧样本用不同的形状和颜色画出,图像如下:
![]()
5.3.1 图像显示
Matplotlib也支持图像的存取和显示,并且和OpenCV一类的接口比起来,对于一般的二维矩阵的可视化要方便很多,来看例子:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
import matplotlib.pyplot as plt
# 读取一张小白狗的照片并显示
plt.figure('A Little White Dog')
little_dog_img = plt.imread('little_white_dog.jpg')
plt.imshow(little_dog_img)
# Z是上小节生成的随机图案,img0就是Z,img1是Z做了个简单的变换
img0 = Z
img1 = 3*Z + 4
# cmap指定为'gray'用来显示灰度图
fig = plt.figure('Auto Normalized Visualization')
ax0 = fig.add_subplot(121)
ax0.imshow(img0, cmap='gray')
ax1 = fig.add_subplot(122)
ax1.imshow(img1, cmap='gray')
plt.show()
|
这段代码中第一个例子是读取一个本地图片并显示,第二个例子中直接把上小节中反傅里叶变换生成的矩阵作为图像拿过来,原图和经过乘以3再加4变换的图直接绘制了两个形状一样,但是值的范围不一样的图案。显示的时候imshow会自动进行归一化,把最亮的值显示为纯白,最暗的值显示为纯黑。这是一种非常方便的设定,尤其是查看深度学习中某个卷积层的响应图时。得到图像如下:
![]()
![]()
只讲到了最基本和常用的图表及最简单的例子,更多有趣精美的例子可以在Matplotlib的官网找到: