resnet 论文笔记

摘要

Deeper neural networks are more difficult to train. We present a residual learning framework to ease the training of networks that are substantially deeper than those used previously. We explicitly reformulate the layers as learning residual functions with reference to the layer inputs, instead of learning unreferenced functions. We provide comprehensive empirical evidence showing that these residual networks are easier to optimize, and can gain accuracy from considerably increased depth.

神经网络越深越难训练。作者提出了一个残差学习的结构，使得很容易的训练更深的网络，而且网络深度大大增加。作者很明确的重新设计当前层，使其学习当前层输入的残差函数，而不是学习其它内容。并提供了充分的实验证据表示残差网络更容易优化，而且可以从很深的网络中获得更好的准确性。

---

作者在摘要里面提到的数据集
ImageNet，CIFAR，COCO
其中前两个是分类，COCO是目标检测和分割，ILSVRC是图像识别挑战赛的缩写，主要用到的数据集是ImageNet，当前这个比赛也会有目标检测和分割

---

介绍

Deep networks naturally integrate low/mid/high level features [50] and classifiers in an end-to-end multi-layer fashion, and the “levels” of features can be enriched by the number of stacked layers (depth). Recent evidence [41, 44] reveals that network depth is of crucial importance, and the leading results [41, 44, 13, 16] on the challenging ImageNet dataset [36] all exploit “very deep” [41] models, with a depth of sixteen [41] to thirty [16]. Many other non-trivial visual recognition tasks [8, 12, 7, 32, 27] have also greatly benefited from very deep models.

深度网络通常整合了低/中/高级别特征，并且使用多层端到端的分类器。这些不同层次的特征可以通过更深的堆叠layer来获得更丰富的特征。最近的证据表明深度非常重要，在ImageNet上的数据集都使用了非常深的模型，其它的
重大的识别任务也都使用非常深的模型获得更好的性能。

Driven by the significance of depth, a question arises: Is learning better networks as easy as stacking more layers? An obstacle to answering this question was the notorious problem of vanishing/exploding gradients [1, 9], which hamper convergence from the beginning. This problem, however, has been largely addressed by normalized initialization [23, 9, 37, 13] and intermediate normalization layers [16], which enable networks with tens of layers to start converging for stochastic gradient descent (SGD) with back-
propagation [22].

在深度重要性的驱动下，出现一个问题：训练一个更好的网络是否像堆叠更多的layer一样容易。主要是由于梯度消失和梯度爆炸导致更深的网络难以收敛。这个问题已经被归一化的初始化和中间归一化layer的策略得到解决，使得网络可以在数十层的时候可以使用SGD的反向传播收敛。

When deeper networks are able to start converging, a degradation problem has been exposed: with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error, as reported in [11, 42] and thoroughly verified by our experiments. Fig. 1 shows a typical example.

更深的网络可以开始收敛，会出现一个退化问题：随着网络的加深，准确性会达到饱和，然后迅速下降。这个下降不是由于过拟合引起的，增加更多的layer反而会得到更大的误差。

The degradation (of training accuracy) indicates that not all systems are similarly easy to optimize. Let us consider a shallower architecture and its deeper counterpart that adds more layers onto it. There exists a solution by construction to the deeper model: the added layers are identity mapping, and the other layers are copied from the learned shallower model. The existence of this constructed solution indicates that a deeper model should produce no higher training error than its shallower counterpart.

这种退化问题表明不是所有的系统都容易优化，考虑一个浅的结构，并在这个浅的模型上加深。存在一个解决方案：增加的层是以同等映射的方式实现
，并且其它层是从学习的更浅的模型中复制过来。这种解决方式表明，更深的模型不应该产生比相应更浅模型跟高的训练误差。

---

作者没说产生他这种退化问题的原因。
这段作者简单的介绍了他的解决方案，先总结一下，再用一个简单粗暴的比喻来描述一下作者的总结方案。

在神经网络中，如果模型越深，效果应该越好。
但是实际上由于梯度消失或者爆炸的问题没有办法加深，不过梯度消失和爆炸的问题可以使用初始化以及中间层初始化的策略解决。（比如xavier 初始化以及kaiming 初始化，何老师自己引用自己=_=）

但是模型更深了以后精度会饱和，然后突然下降。这个问题是不是由梯度消失和爆炸导致的，而是由于退化问题。

作者搞了一个普通的浅层网络，现在想要把这个网络加深。在浅的模型上多加个一个layer，至少不能比加之前性能更差吧？也就是这个新的layer可以啥作用都不起，但是你别给起到负面的作用。

---

In this paper, we address the degradation problem by introducing a deep residual learning framework. Instead of hoping each few stacked layers directly fit a desired underlying mapping, we explicitly let these layers fit a residual mapping. Formally, denoting the desired underlying mapping as H(x), we let the stacked nonlinear layers fit another mapping of F(x) := H(x)−x. The original mapping is recast into F(x)+x. We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.

本文引入深度残差讯息框架来解决退化问题。作者定义底层映射（underlying mapping）表示为H(x)，作者定义了一个堆叠的非线性层去拟合F(x)，这里F(x) = H(x) - x。原始的映射被重新表示为F(x) + x。假设优化残差映射比原始的映射更容易。极端的情况下，如果恒等映射是最优的，那么此时会把残差映射挤压为0，这样的操作更容易实现。

---

上面的翻译没有依照英文原文的内容，里面有几个名词，比较晦涩。是深度学习原理和一些老的概念。
底层映射H(x)，从公式上来看，表示为H(x) = F(x) + x，实际上就是下一个layer想要比上一层学习到更深层次的内容。
这个更深层次的内容表示为F(x)，也就是作者提到的残差映射(residual mapping)。
此处的x就是上一层学习到的内容，如果当前层啥也学不到，即F(x)为0，那么最也可以把上一层学习到的内容拿过来，也就是F(x)为0的情况下，H(x) = x，
这个情况叫做恒等映射（identify mapping)。

---

The formulation of F(x)+x can be realized by feedforward neural networks with “shortcut connections” (Fig. 2). Shortcut connections [2, 34, 49] are those skipping one or more layers. In our case, the shortcut connections simply perform identity mapping, and their outputs are added to the outputs of the stacked layers (Fig. 2). Identity shortcut connections add neither extra parameter nor computational complexity. The entire network can still be trained end-to-end by SGD with backpropagation, and can be easily implemented using common libraries (e.g., Caffe [19]) without modifying the solvers.

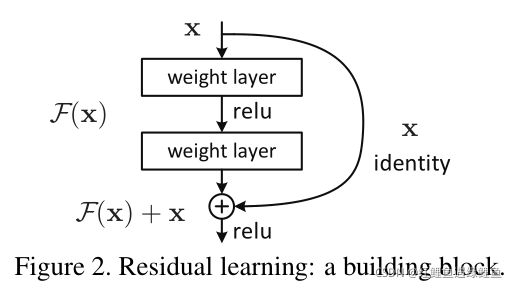
公式F(x) + x 的前向传播方式可以表示成“shortcut connections"的跳跃连接的方式，也就是同等映射的表示方式，如figure 2所示。这样可以使用SGD进行端到端的训练和反向传播。

---

作者后面在cifar，imagenet等数据集上进行了测试，结果很牛逼，不用多说。

相关工作

残差表示

作者的学习残差的思路是从Fisher Vector和VLAD中取得的。经典的机器学习方法,常用于计算机视觉。

shortcut connections

这种连接方式也不是凭空而来，早期训练MLP的时候就有人这么用过，比如将输入直接连接到中间层和输出层，用来解决梯度爆炸和梯度小时的问题，如inception模型。
此外还有highway network，设置了一个gate，这个gate用来控制残差的流入。

---

可见，想有点思路，是要多读论文的 =_=
另外，总读最新的文章是很难了解底层原理的哦

---

深度残差学习

感觉作者好絮叨啊 =_=

残差学习

Let us consider H(x) as an underlying mapping to be fit by a few stacked layers (not necessarily the entire net), with x denoting the inputs to the first of these layers. If one hypothesizes that multiple nonlinear layers can asymptotically approximate complicated functions 2 , then it is equivalent to hypothesize that they can asymptotically approximate the residual functions, i.e., H(x) − x (assuming that the input and output are of the same dimensions). So rather than expect stacked layers to approximate H(x), we
explicitly let these layers approximate a residual function F(x) := H(x) − x. The original function thus becomes F(x)+x. Although both forms should be able to asymptotically approximate the desired functions (as hypothesized), the ease of learning might be different.

这一段的内容作者就是把introduction的部分细说了一下。主要表述为与其堆叠layer去拟合H(x)，不如去让这些layer拟合F(x)，即拟合残差项。

With the residual learning reformulation, if identity mappings are optimal, the solvers may simply drive the weights of the multiple nonlinear layers toward zero to approach identity mappings.

通过增加残差项，如果恒等映射是最优的，那么网络模型会自动的把残差内容挤压成0，来达到恒等射射的目的。

In real cases, it is unlikely that identity mappings are optimal, but our reformulation may help to precondition the problem. If the optimal function is closer to an identity mapping than to a zero mapping, it should be easier for the solver to find the perturbations with reference to an identity mapping, than to learn the function as a new one.

在实际情况下，恒等映射不可能最优，所以肯定会学习到残差。

---

何老师可真是絮叨啊，同一个概念在几个部分翻来覆去的说。倒不如把退化的本质原因好好讲讲。

---

通过shortcut实现恒等映射

将残差学习应用到一些堆叠的层上。给出公式
$y=F(x,\{W_i\})+x$
x表示输入，y表示输出，都是向量形式。
函数F表示需要学习的残差映射。如上面的figure 2中由两层。

$F=W_2\sigma (W_{1}x)$ （1）
其中σ表示ReLU，这里不考虑bias。

F + x公式表示shortcut connection，并且使用element-wise的方式相加的。

公式(1) 没有增加额外的参数也没有增加额外的计算复杂度。在实践中很好用。可以公平的对比发现，plain网络和residual网络拥有相同多的参数，深度，快读以及计算量（除了element-wise以外）

The dimensions of x and F must be equal in Eqn.(1). If this is not the case (e.g., when changing the input/output channels), we can perform a linear projection $W_s$ by the shortcut connections to match the dimensions:

x和F的维度必须相同，如果不同我们可以使用一个线性投影$W_s$，来匹配shortcut connection的纬度。
$y=F(x,\{W_i\})+W_{s}x$ (2)

We can also use a square matrix W s in Eqn.(1). But we will show by experiments that the identity mapping is sufficient for addressing the degradation problem and is economical, and thus W s is only used when matching dimensions.

也可以在公式（1）中使用方阵$W_s$。但是在实验中发现恒等映射解决退化问题最经济使用，因此$W_s$矩阵尽在匹配维度的时候使用。

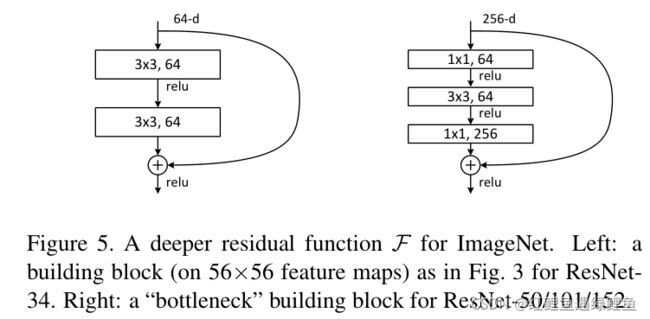
The form of the residual function F is flexible. Experiments in this paper involve a function F that has two or three layers (Fig. 5), while more layers are possible. But if F has only a single layer, Eqn.(1) is similar to a linear layer: $y=W_{1}x+x$, for which we have not observed advantages.

残差函数F的形式很灵活。实验证明F函数两层或者三层最佳，当然更多的层也可以。但是如果只有一层，那么公式（1）就变成了一个线性层了，即
$y=W_{1}x+x$，啥用都不起了。

We also note that although the above notations are about fully-connected layers for simplicity, they are applicable to convolutional layers. The function $F(x,W_i)$ can represent multiple convolutional layers. The element-wise addition is performed on two feature maps, channel by channel.

注意到上面的公式符号都是用全连接层表示的，但是他们也适用于卷积层。函数$F(x,W_i)$可以表示多个卷积层。element-wise在卷积层上表示为逐channel相加。

---

作者解释了一些计算量，参数数量以及在卷积网络中的实现形式。
先说shortcut没有引入额外的计算量，后来又来了一句除了element-wise以外
晕 =_=

网络结构

plain结构

灵感来源于VGG网络。卷积层基本上都是3×3的卷积核，并结合两个简单的设计规则：
对于相同的输出特征图尺寸，layers要有相同的卷积核数量，如果特征图的尺寸减半了，那么调用一个downsampleing的降采样过程，即世界使用一个stride为2的卷积核计算。最后网络以一个average pooling和一个全连接层加上softmax结束。

---

上面的plain网络，可不是resnet，别看晕了，这个网络是为了和resnet进行对比用的，作者想要对比的公平一点 =_=

---

residual结构

这个才是resnet的设计
基于上面的plain 网络，在这个基础上插入shortcut connection。
identity shortcut可以直接使用，当输入和输出有相同的维度。（figure 3的实线）
当维度增加的时候，这里有两个选择（figure 3的虚线）
（A)用padding 0来提升维度。这个操作不会引入额外的参数
（B)使用方程(2)的projection shortcut来匹配维度（使用1×1的卷积）
上面的两个做法，如果遇到特征图的大小出现二倍的情况下，使用stride为2的卷积核。

---

来个知识点
网络的flops是什么，怎么计算？见最后

---

实验

identity vs projection shortcuts

identity shortcuts没有额外的参数假如，使用project shortcuts的形式如上所述包含两种，一种是（A）通过补充pad来扩充维度 （B)project shortcuts用来提高维度，其它的shortcut用来执行identity操作（C)所有shortcut都是用projection

上面三种策略都比plain network要强，这三个相比，C > B > A 原因如下：
We argue that this is because the zero-padded dimensions in A indeed have no residual learning.
作者认为pad 0 的部分没有学习到残差。

C is marginally better than B, and we attribute this to the extra parameters introduced by many (thirteen) projection shortcuts.

C比B略好，作者认为原因是C比B多了不少projection shortcuts。

But the small differences among A/B/C indicate that projection shortcuts are not essential for addressing the degradation problem. So we do not use option C in the rest of this paper, to reduce memory/time complexity and model sizes. Identity shortcuts are particularly important for not increasing the complexity of the bottleneck architectures that are introduced below.

ABC三者的差异表明对于退化问题，projection shortcuts没起到太多作用。
考虑到计算复杂度和模型大小，文中其余部分没使用C。identify shortcuts
对于不增加模型复杂性特别重要，尤其是对比bottleneck结构。

---

这里首次出现bottleneck 结构，结合上面的图和projection shortcut，bottlenect 结构就是projection shortcut的实现方式，下面也说了就是对projection shortcut的替换。

---

Deeper Bottleneck Architectures

Because of concerns on the training time that we can afford, we modify the building block as a bottleneck design 4 . For each residual function F, we use a stack of 3 layers instead of 2 (Fig. 5). The three layers are 1×1, 3×3, and 1×1 convolutions, where the 1×1 layers are responsible for reducing and then increasing (restoring) dimensions, leaving the 3×3 layer a bottleneck with smaller input/output dimensions. Fig. 5 shows an example, where both designs have similar time complexity.

考虑到训练时间，作者修改了bottleneck的设计。对每个残差函数F。作者使用了3层而不是使用两层，如图5所示。线进行1×1的卷积降维。然后使用3×3的卷积，最后使用1×1的卷积提高维度。

The parameter-free identity shortcuts are particularly important for the bottleneck architectures. If the identity shortcut in Fig. 5 (right) is replaced with projection, one can show that the time complexity and model size are doubled, as the shortcut is connected to the two high-dimensional ends. So identity shortcuts lead to more efficient models for the bottleneck designs.

没有额外参数添加的identify shortcut对于bottleneck结构更加重要。如果identity shortcut换成 projection，那么时间夫再度和模型大小会乘2，因为shortcut 连接到了两个高维度的终端。所以identify shortcuts 比bottleneck更有效率。

代码

class BasicBlock(nn.Module):
    expansion = 1

    def __init__(self, in_channel, out_channel, stride=1, downsample=None, **kwargs):
        super(BasicBlock, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=out_channel,
                               kernel_size=3, stride=stride, padding=1, bias=False)
        self.bn1 = nn.BatchNorm2d(out_channel)
        self.relu = nn.ReLU()
        self.conv2 = nn.Conv2d(in_channels=out_channel, out_channels=out_channel,
                               kernel_size=3, stride=1, padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(out_channel)
        self.downsample = downsample

    def forward(self, x):
        identity = x
        if self.downsample is not None:
            identity = self.downsample(x)

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)

        out += identity
        out = self.relu(out)

        return out

上面代码是BasicBlock，一个basicBlock主要包括一个下采样，两个3×3的卷积
下采样在resnet第一次调用BasicBlock时不会使用

class Bottleneck(nn.Module):
    """
    注意：原论文中，在虚线残差结构的主分支上，第一个1x1卷积层的步距是2，第二个3x3卷积层步距是1。
    但在pytorch官方实现过程中是第一个1x1卷积层的步距是1，第二个3x3卷积层步距是2，
    这么做的好处是能够在top1上提升大概0.5%的准确率。
    可参考Resnet v1.5 https://ngc.nvidia.com/catalog/model-scripts/nvidia:resnet_50_v1_5_for_pytorch
    """
    expansion = 4

    def __init__(self, in_channel, out_channel, stride=1, downsample=None,
                 groups=1, width_per_group=64):
        super(Bottleneck, self).__init__()

        width = int(out_channel * (width_per_group / 64.)) * groups

        self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=width,
                               kernel_size=1, stride=1, bias=False)  # squeeze channels
        self.bn1 = nn.BatchNorm2d(width)
        # -----------------------------------------
        self.conv2 = nn.Conv2d(in_channels=width, out_channels=width, groups=groups,
                               kernel_size=3, stride=stride, bias=False, padding=1)
        self.bn2 = nn.BatchNorm2d(width)
        # -----------------------------------------
        self.conv3 = nn.Conv2d(in_channels=width, out_channels=out_channel*self.expansion,
                               kernel_size=1, stride=1, bias=False)  # unsqueeze channels
        self.bn3 = nn.BatchNorm2d(out_channel*self.expansion)
        self.relu = nn.ReLU(inplace=True)
        self.downsample = downsample

    def forward(self, x):
        identity = x
        if self.downsample is not None:
            identity = self.downsample(x)

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu(out)

        # conv3是1×1的卷积
        out = self.conv3(out)
        out = self.bn3(out)

        out += identity
        out = self.relu(out)

        return out

上面是bottleneck，可以看到conv1的kernel = 1,首先会对channel进行压缩，然后执行conv2进行3×3的卷积运算，在使用conv3将channel扩大

class ResNet(nn.Module):

    def __init__(self,
                 block,
                 blocks_num,
                 num_classes=1000,
                 include_top=True,
                 groups=1,
                 width_per_group=64):
        super(ResNet, self).__init__()
        self.include_top = include_top
        self.in_channel = 64

        self.groups = groups
        self.width_per_group = width_per_group

        self.conv1 = nn.Conv2d(3, self.in_channel, kernel_size=7, stride=2,
                               padding=3, bias=False)
        self.bn1 = nn.BatchNorm2d(self.in_channel)
        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)

        # 第一层的stride是1
        self.layer1 = self._make_layer(block, 64, blocks_num[0]) # 3
        self.layer2 = self._make_layer(block, 128, blocks_num[1], stride=2)
        self.layer3 = self._make_layer(block, 256, blocks_num[2], stride=2)
        self.layer4 = self._make_layer(block, 512, blocks_num[3], stride=2)
        if self.include_top:
            self.avgpool = nn.AdaptiveAvgPool2d((1, 1))  # output size = (1, 1)
            self.fc = nn.Linear(512 * block.expansion, num_classes)
        
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')

    def _make_layer(self, block, channel, block_num, stride=1):
        downsample = None
                # block 如果是BasicBlock的expansion是1 in_channels固定是64 输出的channel只有第一个是64，也就是BasicBlock的首个layer不会执行；
        # 所有的BottleneckBlock会调用downshample
        if stride != 1 or self.in_channel != channel * block.expansion:
            '''
            print("in channel:")
            print (self.in_channel)
            print(block.expansion)
            print("stride :")
            print(stride)
            '''
            downsample = nn.Sequential(
                nn.Conv2d(self.in_channel, channel * block.expansion, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(channel * block.expansion))

        layers = []
        layers.append(block(self.in_channel,
                            channel,
                            downsample=downsample,
                            stride=stride,
                            groups=self.groups,
                            width_per_group=self.width_per_group))
        self.in_channel = channel * block.expansion

        for _ in range(1, block_num):
            layers.append(block(self.in_channel,
                                channel,
                                groups=self.groups,
                                width_per_group=self.width_per_group))

        return nn.Sequential(*layers)

    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.maxpool(x)

        x = self.layer1(x)
        
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.layer4(x)

        if self.include_top:
            x = self.avgpool(x)
            x = torch.flatten(x, 1)
            x = self.fc(x)

        return x


def resnet34(num_classes=1000, include_top=True):
    # https://download.pytorch.org/models/resnet34-333f7ec4.pth
    return ResNet(BasicBlock, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)


def resnet50(num_classes=1000, include_top=True):
    # https://download.pytorch.org/models/resnet50-19c8e357.pth
    return ResNet(Bottleneck, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)


def resnet101(num_classes=1000, include_top=True):
    # https://download.pytorch.org/models/resnet101-5d3b4d8f.pth
    return ResNet(Bottleneck, [3, 4, 23, 3], num_classes=num_classes, include_top=include_top)


def resnext50_32x4d(num_classes=1000, include_top=True):
    # https://download.pytorch.org/models/resnext50_32x4d-7cdf4587.pth
    groups = 32
    width_per_group = 4
    return ResNet(Bottleneck, [3, 4, 6, 3],
                  num_classes=num_classes,
                  include_top=include_top,
                  groups=groups,
                  width_per_group=width_per_group)


def resnext101_32x8d(num_classes=1000, include_top=True):
    # https://download.pytorch.org/models/resnext101_32x8d-8ba56ff5.pth
    groups = 32
    width_per_group = 8
    return ResNet(Bottleneck, [3, 4, 23, 3],
                  num_classes=num_classes,
                  include_top=include_top,
                  groups=groups,
                  width_per_group=width_per_group)

上面是整个resnet的构建

总结

需要学到的内容，深度网络无法达到更深的原因不是因为梯度消失，这点已经可以通过初始化的方式解决，原因是退化。

resnet的构建思想，包括identity shortcut和bottleneck shortcut，两种方式都是使得网络学习残差，其中bottleneck 通过对channel进行先压缩再计算，再扩展channel的方式减少计算和模型大小。

在较浅的网络中，如resnet34使用basicBlock，而在较深的网络，如resnet50和resnet101使用bottleneck，可以节约计算提升性能

来自知乎：https://www.zhihu.com/question/65305385

FLOPS：注意全大写，是floating point operations per second的缩写，意指每秒浮点运算次数，理解为计算速度。是一个衡量硬件性能的指标。

FLOPs：注意s小写，是floating point operations的缩写（s表复数），意指浮点运算数，理解为计算量。可以用来衡量算法/模型的复杂度。

考虑FLOPs

Ci=input channel, k=kernel size, HW=output feature map size, Co=output channel.
MAC 表示加法乘法：y = ax + b

那么输入的特征图的计算公式为：
$(2\times C_i\times K^2-1)\times H\times W\times C_o$
考虑bias时有-1
理解上面的公式封面两步，第一个计算出输出特征图的一个点，然后乘以
HWCo，拓展到整个输出特征图

同理，全连接层：
$(2\times I-1）\times O$
I表示输入神经元个数，O表示输出神经元个数，2是因为一个MAC有两个操作，减1不考虑bias