1.概述
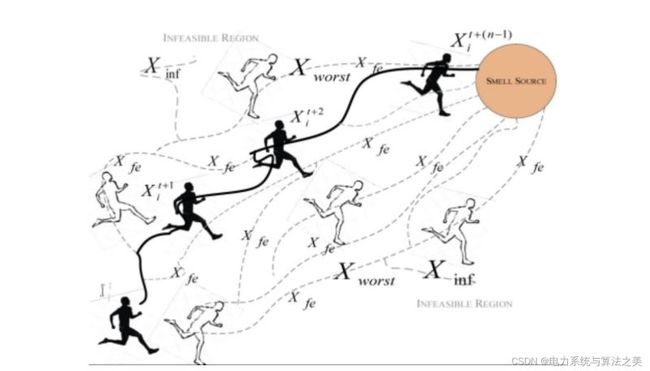
嗅觉剂优化是一种新颖的优化算法,旨在模仿气味分子源尾随的药剂的智能行为。该概念分为三个阶段(嗅探,尾随和随机)是独特且易于实现的。此上传包含 SAO 在 37 个 CEC 基准测试函数上的实现。
2.37 个 CEC 基准测试函数代码
function [lb,ub,dim,fobj] = Select_Function(F)
switch F
case 'F1'
%Admijan
fobj = @F1;
lb=[-1 -1];
ub=[2 1];
dim=2;
case 'F2'
%Beale
fobj = @F2;
dim=2;
lb=-4.5*ones(1,dim);
ub=4.5*ones(1,dim);
case 'F3'
%Bird
fobj = @F3;
dim=2;
lb=-2*pi*ones(1,dim);
ub=2*pi*ones(1,dim);
case 'F4'
%Bohachevsky
fobj = @F4;
dim=2;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F5'
% Booth
fobj = @F5;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F6'
%Branin RCOS1
fobj = @F6;
lb=[-5,0];
ub=[10, 15];
dim=2;
case 'F7'
%Branin RCOS2
fobj = @F7;
dim=2;
lb=-5*ones(1,dim);
ub=15*ones(1,dim);
case 'F8'
%Brent
fobj = @F8;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F9'
%Bukin F2
fobj = @F9;
dim=2;
lb=[-15 -3];
ub=[-5 3];
case 'F10'
%six-hump
fobj = @F10;
dim=2;
lb=-5*ones(1,dim);
ub=5*ones(1,dim);
case 'F11'
%Chichinadze
fobj = @F11;
dim=2;
lb=-30*ones(1,dim);
ub=30*ones(1,dim);
case 'F12'
%Deckkers-Aarts
fobj = @F12;
dim =2;
lb=-20*ones(1,dim);
ub=20*ones(1,dim);
case 'F13'
%Easom
dim=2;
fobj=@F13;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F14'
%Matyas
fobj = @F14;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F15'
%McComick
fobj = @F15;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F16'
%Michalewicz2
fobj = @F16;
dim=2;
lb=0*ones(1,dim);
ub=pi*ones(1,dim);
case 'F17'
%Quadratic
fobj = @F17;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F18'
%Schaffer
dim=2;
fobj = @F18;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F19'
%StyblinskiTang
fobj = @F19;
dim=2;
lb=-5*ones(1,dim);
ub=5*ones(1,dim);
case 'F20'
%Box-Betts
fobj = @F20;
dim=3;
lb=[0.9 9 0.9];
ub=[1.2 11.2 1.2];
case 'F21'
%Colville
fobj = @F21;
dim=4;
lb=-1*ones(1,dim);
ub=1*ones(1,dim);
case 'F22'
%Csendes
fobj = @F22;
dim=4;
lb=-1*ones(1,dim);
ub=1*ones(1,dim);
case 'F23'
% Michalewicz 5
fobj = @F23;
dim=5;
lb=0*ones(1,dim);
ub=pi*ones(1,dim);
case 'F24'
%Miele Cantrell
dim=4;
fobj = @F24;
lb=-1*ones(1,dim);
ub=1*ones(1,dim);
case 'F25'
% Step
fobj = @F25;
dim=5;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F26'
%Michalewicz
fobj = @F26;
dim=10;
lb=0*ones(1,dim);
ub=pi*ones(1,dim);
case 'F27'
%Shubert
fobj = @F27;
dim=5;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F28'
%Ackley
dim=30;
fobj = @F28;
lb=-32*ones(1,dim);
ub=32*ones(1,dim);
case 'F29'
%Brown
fobj = @F29;
dim=30;
lb=-1*ones(1,dim);
ub=4*ones(1,dim);
case 'F30'
%Ellipsoid
dim=2;
fobj = @F30;
lb=-5.12*ones(1,dim);
ub=5.12*ones(1,dim);
case 'F31'
% Grienwank
fobj = @F31;
dim=30;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F32'
%Mishra
fobj = @F32;
dim=30;
lb=0*ones(1,dim);
ub=1*ones(1,dim);
case 'F33'
%Quartic
dim=30;
fobj = @F33;
lb=-1.28*ones(1,dim);
ub=1.28*ones(1,dim);
case 'F34'
%Rastrigin
fobj = @F34;
dim=30;
lb=-5.12*ones(1,dim);
ub=5.12*ones(1,dim);
case 'F35'
%Rosenbrock
fobj = @F35;
dim=30;
lb=-30*ones(1,dim);
ub=30*ones(1,dim);
case 'F36'
% Salomon
fobj = @F36;
dim=30;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F37'
%Sphere
fobj = @F37;
dim=30;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
end
end
function o=F1(x)
% Adjiman
o=(cos(x(:,1)).*sin(x(:,2))-x(:,1)./(x(:,2).^2+1));
end
function o=F2(x)
% Beale
o=(1.5-x(:,1)+(x(:,1).*(x(:,2)))).^2+(2.25-x(:,1)+(x(:,1).*(x(:,2)).^2)).^2+...
(2.625-x(:,1)+(x(:,1).*(x(:,2)).^3)).^2;
end
function o=F3(x)
% Bird
o=sin(x(:,2)).*(exp(1-cos(x(:,1))).^2)+cos(x(:,1)).*(exp(1-sin(x(:,2))).^2)...
+(x(:,1)+(x(:,2))).^2;
end
function o=F4(x)
% Bohachevsky
W=0;
[a,dim]=size(x);
for i=1:dim-1
W=W+x(:,i).^2+2.*x(:,i+1).^2-0.3.*cos(3.*pi.*x(:,i+1))-0.4.*cos(4.*pi.*(x(:,i+1)))+0.7;
end
o=W;
end
function o=F5(x)
%Booth
o=(x(:,2)-(5.1*x(:,1).^2/(4*pi*2))+(5*x(:,1)/pi)-6).^2+...
10*(1-1/(8*pi)).*cos(x(:,1))+10;
end
function o=F6(x)
% Branin RCOS 1
o=(x(:,2)-(5.1*x(:,1).^2/(4*pi*2))+(5*x(:,1)/pi)-6).^2+...
10*(1-1/(8*pi)).*cos(x(:,1))+10;
end
function o=F7(x)
% Branin RCOS 2
a=1; b=5.1/(4*pi^2); c=5/pi; d=6; e=10; g=1/(8*pi);
f1=a*(x(:,2)-b*x(:,1).^2+c*x(:,1)-d).^2;
f2=e*(1-g)*cos(x(:,1)).*cos(x(:,2));
f3=log(x(:,1).^2+x(:,2)+1);
o=-1/(f1+f2+f3+e);
end
function o=F8(x)
%Brent
o=(x(:,1)+10).^2+(x(:,1)+10).^2+exp(-x(:,1).^2-x(:,2).^2);
end
function o=F9(x)
%Bukin F2
o=(abs(x(:,1)-0.01.*x(:,2).^2))+0.01.*abs(x(:,2)+10);
end
function o=F10(x)
%Camel Six Hump
o=(4-2.1*x(:,1).^2+(x(:,1).^4)/3).*x(:,1).^2+x(:,1).*x(:,2)+...
(4*x(:,2).^2-4).*x(:,2).^2;
end
function o=F11(x)
%Chichinadze
o=x(:,1).^2-12*x(:,1)+11+10*cos(pi*x(:,1)/2)+8*sin(5*pi*x(:,1)/2)-...
((1/5)^0.5)*exp(-0.5*(x(:,2)-0.5).^2);
end
function o=F12(x)
% Deckkers-Aarts
o=10^5*x(:,1).^2+x(:,2).^2-(x(:,1).^2+x(:,2).^2).^2+...
10^(-5)*(x(:,1).^2+x(:,2).^2).^4;
end
function o = F13(x)
% Easom
o=-cos(x(:,1)).*cos(x(:,2)).*exp(-(x(:,1)-pi).^2-(x(:,2)-pi).^2);
end
function o=F14(x)
% Evaluate Matyas
o=0.26*(x(:,1).^2+x(:,2).^2)-0.48*x(:,1).*x(:,2);
end
function o=F15(x)
% McCormick
o=mccormick(x);%
end
function o=F16(x)
% Michalewicz2
[~,d]=size(x);
W=0;
for i=1:d
W=sin(x(:,1)).*sin(i*x(:,i).^2/pi).^2*d;
end
o=-W;
end
function o=F17(x)
% Quadratic
o=-3803.84-138.08*x(:,1)-232.92*x(:,2)+128.08*x(:,1).^2+203.64*x(:,2).^2+182.25*x(:,1).*x(:,2);
end
function o=F18(x)
% Evaluate Schaffer
[~,d]=size(x);
w=0;
for i=1:d-1
w=w+((x(i).^2+x(i+1).^2).^.5).*(sin(50.*(x(i).^2+x(i+1).^2).^0.1)).^2;
end
o=w;
end
function o=F19(x)
% Styblinki's Tang
[~,d]=size(x);
W=0;
for i=1:d
W=W+(x(:,i).^4-16.*x(:,i).^2+5.*x(:,i));
end
o=W.*0.5;
end
function o=F20(x)
% Box-Betts
[~,d]=size(x);
W=0;
for i=1:d
g=exp(-0.1.*(i+1)).*x(:,1)-exp(-0.1.*(i+1)).*x(:,2)-((exp(-0.1.*(i+1)))-exp(-(i+1)).*x(:,3));
W=W+g.^2;
end
o=W;
end
function o=F21(x)
% Colville
o=100*(x(:,1)-x(:,2).^2).^2+(1-x(:,1)).^2+90*(x(:,4)-x(:,3).^2).^2+...
(1-x(:,3)).^2+10.1*((x(:,2)-1).^2+(x(:,4)-1).^2)+...
19.8*(x(:,2)-1).*(x(:,4)-1);
end
function o=F22(x)
% Csendes
[~,d]=size(x);
aa=0;
for i=1:d
aa=aa+x(:,i).^6.*(2+sin(1/x(:,i)));
end
o=aa;
end
function o=F23(x)
% Michalewicz 5
[~,d]=size(x);
W=0;
for i=1:d
W=sin(x(:,1)).*sin(i*x(:,i).^2/pi).^2*d;
end
o=-W;
end
function o=F24(x)
%Miele Cantrell
o=(exp(-x(:,1))-x(:,2)).^4+100*(x(:,2)-x(:,3)).^6+...
(tan(x(:,3)-x(:,4))).^4+x(:,1).^8;
end
function o=F25(x)
% Evaluate Step
[~,d]=size(x);
W=0;
for i=1:d
W=W+(floor(x(:,i)+0.5)).^2;
end
o=W;
end
function o=F26(x)
% Evaluate Michalewicz 10
[~,d]=size(x);
W=0;
for i=1:d
W=sin(x(:,1)).*sin(i*x(:,i).^2/pi).^2*d;
end
o=-W;
end
function o=F27(x)
% shubert
[~,d]=size(x);
s1=0;
s2=0;
for i = 1:d
s1 = s1+i*cos((i+1)*x(1)+i);
s2 = s2+i*cos((i+1)*x(2)+i);
end
o = s1*s2;
end
% F28--Ackley
function o = F28(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
function o=F29(x)
[~,d]=size(x);
% Brown
a=0;
for i=1:d-1
a=(x(:,i).^2).^(x(:,i+1)+1)+(x(:,i+1).^2).^(x(:,i).^2+1);
end
o=a;
end
function o=F30(x)
% Ellipsoid
[~,d]=size(x);
W=0;
for i=1:d
W=W+i.*x(:,1).^2;
end
o=W;
end
%Grienwank
function o=F31(x)
o=griewank(x);
end
function o=F32(x)
% Mishra
[~,d]=size(x);
a=0;
for i=1:d-1
a=a+x(:,i);
end
aa=d-a;
b=0;
for j=1:d-1
b=b+x(:,j);
end
W=abs((1+d-b).^aa);
o=W;
end
% --Quartic
function o = F33(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
%Rastrigin
function o=F34(x)
o=rastrigin(x);
end
% Rosenbrock
function o = F35(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
function o=F36(x)
% salomon
x2 = x.^2;
sumx2 = sum(x2, 2);
sqrtsx2 = sqrt(sumx2);
o = 1 - cos(2 .* pi .* sqrtsx2) + (0.1 * sqrtsx2);
end
function o = F37(x)
%Sphere
o=sum(x.^2);
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end
3.F1 Matlab代码仿真
到此这篇关于基于Matlab实现嗅觉优化算法的示例代码的文章就介绍到这了,更多相关Matlab嗅觉优化算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!