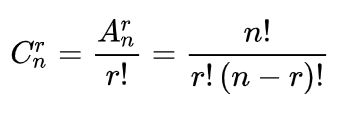第十二届蓝桥杯python

结果填空

A.卡片

算法思路：其实只需要看"1"的卡片，因为按顺序，1的卡片最先用完。

n=1#卡片1的使用情况
x=1#能拼到的数
while n<2021:
    x+=1
    n+=str(x).count("1")
print(x)#3181

B.直线

算法思路：利用两点式直线方程

(y1-y2) * x +(x2-x1) * y +( x1 * y2 - x2 * y1)=0

最后算出的结果是Ax+By+C=0的格式，只要约分后的A、B、C不相同即可视为不同直线

ls=[]
for i in range(20):
    for j in range(21):
        ls.append((i,j))
def gcd(x,y):
    if y==0:
        return x
    return gcd(y,x%y)
ans=set()
for i in range(len(ls)-1):
    x1,y1=ls[i]
    for j in range(i+1,len(ls)):
        x2,y2=ls[j]
        A=y1-y2
        B=x2-x1
        C=x1*y2-x2*y1
        k=gcd(gcd(A,B),C)
        ans.add((A/k,B/k,C/k))
print(len(ans))#40257

B.双阶乘

算法思路：注意后5位的求法，//是取前面的数，%是求后面的数，注意区分使用

sum=1
for i in range(1,2022,2):
    sum*=i
    sum=sum%100000#求后五位数是用求余
print(sum)#59375

B.纯质数

算法思路：枚举 数论
对代码进行模块化，判断纯质数定义两个函数，纯数＋质数(纯数运行快，先判断。质数运行慢)
PS:要先理好算法的逻辑，思考怎么样的顺序可以运算快一点，简单点。

#纯数
def pure(x):
    while x:
        if x%10 in [0,1,4,6,8,9]:#个位数不是质数
            return False
        x//=10
    return True
#质数
def prime(x):
    for i in range(2,int(x**0.5)+1):
        if x%i==0:    #能被1和自身整除的数才是质数
            return False
    return True
#纯质数
cnt=0
for i in range(1,20210606):
    if pure(i) and prime(i):#注意先判断纯数，再判断质数
        print(i)
        cnt+=1
print(cnt)#1903

C.货物摆放

算法思路：求出这个数所有的因子(只需要算到开根号位置就行)，然后依次遍历判断，记录总数。

import math
n= 2021041820210418
nums=set()#集合比列表快
for i in range(1,int(math.sqrt(n))+1):
    if n%i==0:#可以整除
        # 保存约数
        nums.add(i)
        nums.add(n//i)
count=0
for x in nums:
    for y in nums:
        for z in nums:
            if x*y*z==n:
                count+=1
print(count)#2430

C.格点

太简单了，暴力

cnt=0
for x in range(1,2022):
    for y in range(1,2022):
        if x*y<=2021:
            cnt+=1
print(cnt)#15698

C.完全日期(!!!)

算法思路：枚举+日期模块

from datetime import timedelta,datetime
#日期初始化
start=datetime(2001,1,1)
end=datetime(2021,12,31)
delta=timedelta(1)
#分解整数模块
def abc(x):
    ans=0
    while x:
        ans+=x%10
        x//=10
    return ans
#循环遍历
cnt=0
while start<=end:
    sum=abc(start.year)+abc(start.month)+abc(start.day)
    if sum in [2,4,9,16,25,36,49,64,81,100]:
        cnt+=1
    start+=delta
print(cnt)#977

D.路径

算法思路：动态规划(参考大佬博客)

def lcm(a,b):
    if b>a:
        a,b=b,a
        ab=a*b
        while b>0:
            b,a=a%b,b
        return ab//a
n=2021
dp=[float('inf')]*(n+1)
for i in range(1,22):#初始化i在1到22范围内的值
    dp[i]=i
for i in range(22,n+1):#计算后面点的值
    for j in range(1,22):
        dp[i]=min(dp[i],dp[i-j]+lcm(i-j,i))#每一次保留最小的
print(dp[n])#10266837

D. 整数分解

算法思路：
方法一：五层for循环暴力破解，时间复杂度O(n^ 5)=2021^ 5不可行
方法二：用排列组合的隔板法 (引用一位大佬博客的方法)

print(2020*2019*2018*2017//4//3//2//1)
#691677274345

D.最小权值

算法思路：动态规划(参考大佬博客)，DP五步

dp=[0]+[float("inf")]*2021#i为结点编号 初始化:空结点+2021个无穷结点
for i in range(1,2022):
    for j in range(i):
        dp[i]=min(dp[i],1+2*dp[j]+3*dp[i-j-1]+j*j*(i-j-1))#递推公式
print(dp[2021])#2653631372

E.回路计数

困难题
考察题型：动态规划 数论
涉及知识点：状态压缩DP 互质
参考题解

E.城邦

困难题
考察题型：图论
涉及知识点：最小生成树-并查集
参考题解

E.大写

算法思路：要有实打实的基础，要多拓展一下
这次考string.upper() ，下次可能会考 .lower() .capitalize() .isdigit() .count()···
复习python的字符串内建函数菜鸟教程

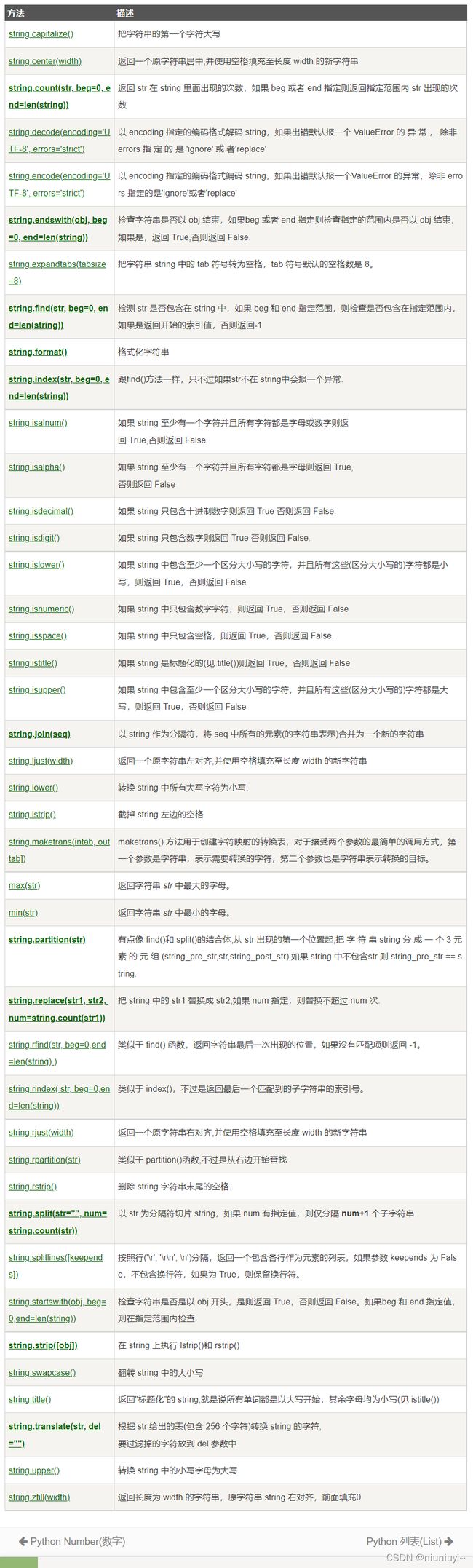
print(input().upper())

F.时间显示

算法思路：

思路分析：

主要用到两个时间函数，简单到可以3行搞定（＾∀＾●）ﾉｼ

当然前提是你得知道几个关键的时间函数。

先转换成时间对象格式，再转换成可读字符串格式。

time.gmtime() #转换为time.struct_time类型的时间对象的秒数

time.asctime() #返回一个可读形式的字符串 Tue Feb 17 09:42:58 2009

"""方法一.时间模块"""
import time
n=int(input())
print(time.asctime(time.gmtime(n//1000))[11:19])
#//1000是指忽略毫秒
#[11:19]表示只取出时间部分 如09:42:58

"""方法二.数学关系计算"""
n=1618708103123#目标:把ms变为s,min,h
n//=1000#ms->s
n%=24*60*60#s除去24h
s=n%60#s除去1分钟
n//=60#s->min
h=n//60#min->h
m=n%60#min除去1h
print("{:02d}:{:02d}:{:02d}".format(h,m,s))

F.小平方

n=int(input())#input为字符串类型
count=0
for i in range(1,n):
    if i*i%n<n//2:
        count+=1
print(count)

F.123

算法思路：暴力枚举，先得部分的分

nums=[]
cnt=0
for i in range(1000):
    cnt+=1
    for j in range(1,cnt+1):
        nums.append(j)

n=int(input())
ls=[]
for i in range(n):
    l,r=map(int,input().split())
    ls.append(sum(nums[l-1:r]))
for i in ls:
    print(i)

G.杨辉三角形

算法思路：枚举 查找 数论
组合数公式

参考题解

#组合值模板
def C(a,b):
    res=1
    fz=a#分子
    for fm in range(1,b+1):#1~b
        res=res*fz//fm#递推公式=分子//分母
        fz-=1
        if res>n:
            return res
    return res
def check(k):# k:斜行
    l,r=2*k,n#赋初值left:2k right:n
    while l<r:
        mid=l+r>>1 #>>1相当于(l+r)//2
        if C(mid,k)>=n:
            r=mid
        else:
            l=mid+1

    if C(r,k)!=n:
        return False
    print(r*(r+1)//2+k+1)#查找位置
    return True

n=int(input())
if n==1:
    print(1)
else:
    for k in range(16,0,-1):#从16斜行枚举
        if check(k)==True:
            break

G.完全平方数

算法思路：
关键是找到唯一分解定理下的奇数个的质数因子。

唯一分解定理：一个合数（2的倍数）可以用一种最小质数的积的形式表示。

比如：6=23 12=22*3

质数因子：又是质数又是因子

质数：2，3，5，7，11······

因子：比如6的因子:1,2,3,6

6的质因子就是：2，3

具体思路：给奇数个质数因子再乘上一个该质数就可以让这个数变成完全平方数，

ans=n*x

36=12*3

36=2 * 2 * 3 *3

举个栗子：对于偶数个质因子“2”，因为2*2已经配对成完全平方数4，所以不需要计数。

只需要统计奇数个质因子是一个“3”，最后nx=123，答案ans=完全平方数36了。

n=int(input())
x=1
for i in range(2,int(n**0.5)+1):
    cnt=0
    while n%i==0:
        cnt+=1
        n//=i
    if cnt%2==1:#分解因子是奇数个数
        x*=i#答案乘是质数因子x*=3
print(n*x)

G.冰山

思考… …

H.左孩子右兄弟

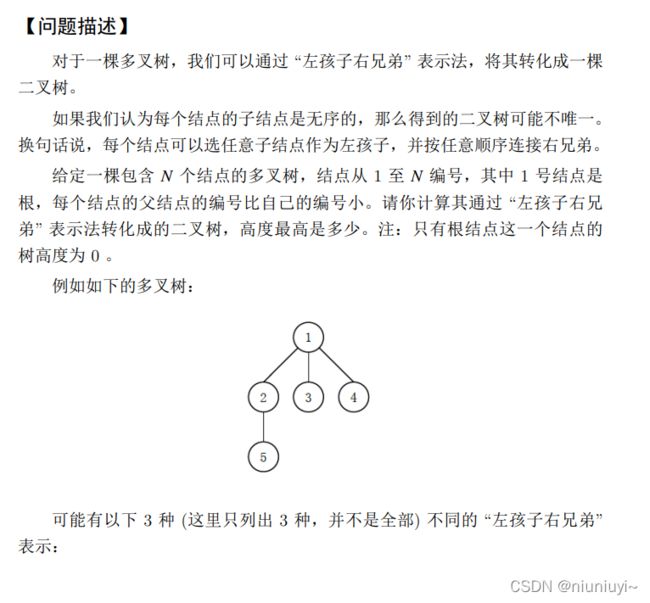
算法思路：暴力破解
根据题意，定义一个树节点类，再初始化结点。
定义一个递归函数，求树的最大高度，最后遍历即可。
一步步转化，求二叉树最高高度->孩子结点个数

可以发现左孩子右兄弟的存储方法，对于树上的一个节点，它的所有儿子都会按照某种顺序依次成为它的右儿子，右儿子的右儿子，右儿子的右儿子的右儿子…依次类推深度不断增加。所以这里就有一个递归的结论：对于一个节点，只有把它的所有儿子形成的子树中，转化为二叉树深度最深的儿子放到最下边，才会最优。所以对于每个结点的所有儿子顺序选择，只需要选择它的儿子形成的子树中转化成二叉树高度最高的放到最后边就能得到最优答案。
树形DP：

f[u]：以点 u 为根节点，通过 “左孩子右兄弟” 表示法转化成二叉树后的最大高度；

f[u] = 子节点数量 + 子树转化为二叉树后的最大高度；

#二维列表法
a=[[] for i in range(100001)]#测试数据最大为十万
n=int(input())
for i in range(2,n+1):
    father=int(input())
    a[father].append(i)
#树型DP
def dfs(t):
    ans=0
    for i in range(len(a[t])):
        ans=max(ans,dfs(a[t][i])+len(a[t]))
    return ans
print(dfs(1))#从根节点开始遍历

#树形结构版
#定义结点类
class node():
    def __init__(self,val):
        self.val=val#父结点值
        self.child=[]#结点孩子
tree=[None,node(val=0)]#初始化树
#初始化树列表
n=int(input())
for i in range(2,n+1):
    m=int(input())
    tree.append(node(val=m))
    tree[m].child.append(i)
#最大长度-递归函数
def maxlen(n:node):
    if len(n.child)==0:  #无孩子，高度为0
        return 0
    else:
        return len(n.child)+max(maxlen(tree[temp]) for temp in n.child)
print(maxlen(tree[1]))

H.负载均衡

思考… …

H.和与乘积

思考… …

I.异或数列

思考… …

I.国际象棋

思考… …

I.二进制问题

思考… …

J.括号序列

算法思路:动态规划

思考… …

Mod=(int)(1e9+7)

def add(x,y):
    return (x+y)%Mod

def brackets():
    f=[[0 for i in range(n+10)] for i in range(n+10)]
    f[0][0]=1

    for i in range(1,n+1):
        if str[i]=='(':
            for j in range(1,n+1):
                f[i][j]=f[i-1][j-1]
        else:
            f[i][0]=add(f[i-1][0],f[i-1][1])
            for j in range(1,n+1):
                f[i][j]=add(f[i-1][j+1],f[i][j-1])
    for i in range(n+1):
        if f[n][i]:
            return f[n][i]

str=list(input())
n=len(str)

str.insert(0,0)#使目标字符串从下标1开始
ans_l=brackets()

str.reverse()
for i in range(n):
    if str[i]=='(':
        str[i]=')'
    else:
        str[i]='('
str.insert(0,0)#使目标字符串下标从1开始
ans_r=brackets()

print(ans_l*ans_r%Mod)

J.完美序列

思考… …

J.翻转括号序列

思考… …

省赛题解