三维重建——相机几何参数标定
点击上方“计算机视觉工坊”,选择“星标”
干货第一时间送达
三维重建——相机几何模型和投影矩阵中,我们已经看到了透视相机的成像模型和相机矩阵:
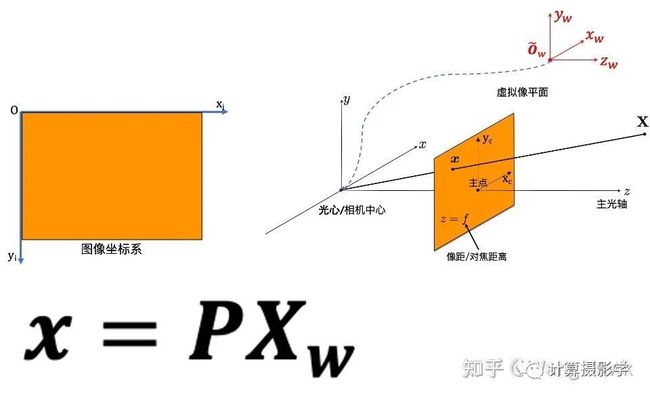
现在我们来思考一个问题,如果已知一系列3D点和其对应的2D图像点,如何通过上述模型求得相机矩阵P,进而求得相机的内参、外参的详细参数?事实上,这个过程就叫做相机的几何参数标定。这个问题有多种解决方法,我今天将要介绍基本的线性求解方法,和更加准确的非线性求解方法。
本文同步发表在我的微信公众号和知乎专栏“计算摄影学”,欢迎扫码关注,转载请注明作者和来源
一. 线性求解方法
1.1 基础表达式
展开上面的成像公式,可以得到。正如我所介绍的,对于一般的透视相机,其相机矩阵P一共有11个自由度,这里我们省略掉了 ![]() 的各元素的下标w。
的各元素的下标w。
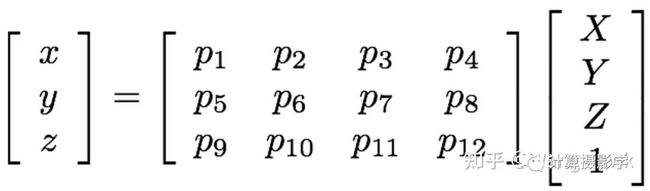
简单的把P矩阵中的每一行表示为piT, 把三维点向量表示为X,我们有

稍加变换,我们可以得到下面的式子,这里x'和y’代表成像点的非齐次坐标
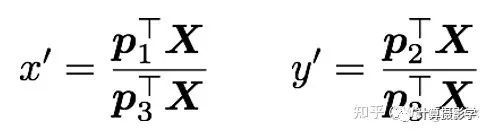
虽然上面这两个式子是非线性的,但对这两个式子做一点基本的数学变换,可以得到下面两个线性方程。也说明,如果已知一对点坐标,就可以得到两个线性方程,注意这里各个元素的维度:
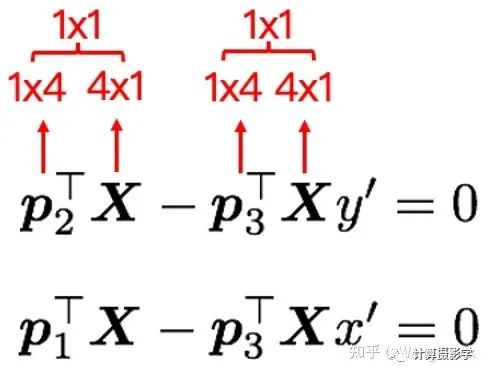
我们可以很简单的把这两个式子表达为矩阵和向量相乘的形式
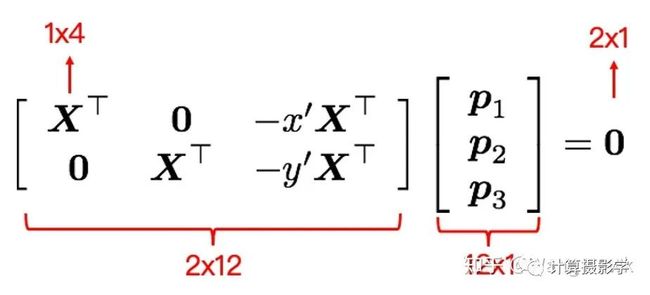
当我们有N对点时,可以组成更多线性方程:
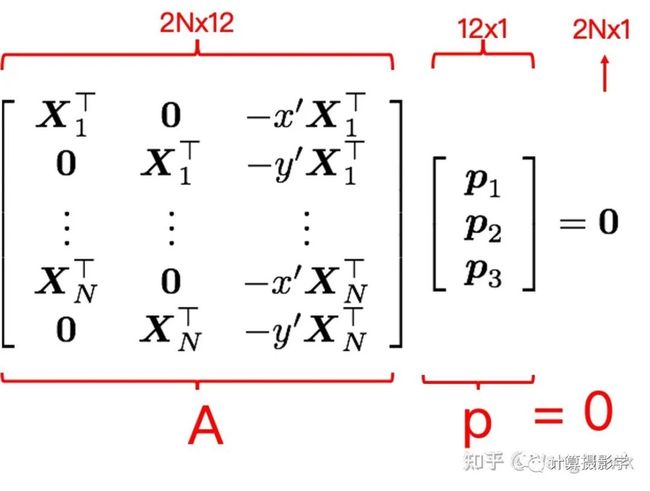
这个式子我们也可以简单的表示为Ap = 0的形式。
1.2 求解方式
基本解:
我们知道,透视相机矩阵有11个自由度,一对点提供了2个方程,这意味着我们知道5.5对点,就可以求出相机矩阵P。你可能会想,5.5对是什么鬼?这实际上是指,最后一对匹配点,我们仅仅需要X->x'或者X->y'即可。
超定解与代数误差:
当然,当点的数量很少时,各种噪声都很大。所以一般利用更多的点,构成超定方程组来求解,减轻噪声的影响。这个时候,因为测量点坐标的误差,同时点对的数量大于6个,所以上述式子是没有唯一解的,比如p=0就是一个解,但这个解显然不是我们想要的。所以我们需要通过加入某种约束条件,然后通过最小化||Ap||来求解。
可以选择的约束条件有多种,我们选择了||p||^2=1。那么整个过程,可以转换为如下的表达式:
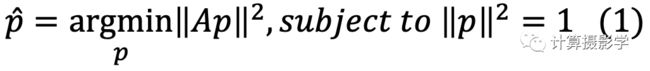
这里面我们优化的就是所谓的代数误差,或者代数距离。以上表达式的经典求解方法是采用SVD分解,将A分解为3个特别矩阵的乘积:
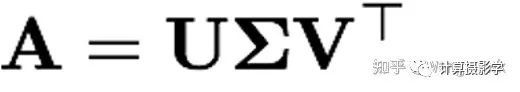
其中,V矩阵是正交矩阵,而∑是一个对角据阵,对角元素都是非负的。那么上式中的解p就是V中对应着最小奇异值的那一列。如果SVD分解时已经将∑的对角元素从大到小排列,那么解p实际上就是V的最后一列。
1.3 数据归一化
我们在1.2节所看到的通过优化代数距离来求解相机矩阵的方法称为直接线性变换法(DLT:Direct Linear Transformation), 在《计算机视觉中的多视角几何》一书的4.4节中,专门花了很多篇幅来说明这个方法不具有变换不变性。也就是说它的求解结果取决于坐标系的选择,当用不同的方式来表达2D点和3D点的坐标时,求取的相机矩阵是不一样的。特别是,2D点坐标是用像素来表达的,3D点坐标则用类似于毫米这样的单位来表达,它们的值域差异较大,使得在使用DLT时很容易放大数值误差。具体的理论分析我这里略过,大家可以阅读上面说的参考内容。我想告诉你的是,在应用DLT算法时应该首先对2D点和3D点的坐标值进行归一化变换,并在计算完成后做一些反变换,才能得到最佳的结果。
1.4 完整的DLT求解过程
回到投影公式,公式的左、右分别有2D点坐标和3D点坐标。假设我们现在有>=6对点,需要求得相机矩阵P,下面阐述完整的过程:

第1步:2D点坐标归一化
计算一个相似变换T(由平移和缩放组成),将所有2D点x变为x'=Tx, 到达如下目的
变换后的2D点的中心坐标变为(0,0)T
变换后的2D点到(0,0)T点的平均距离为\sqrt(2)
第2步:3D点坐标归一化
3D点坐标归一化分为两种情况。
情况1:如果所有3D点的深度变化不大(例如同一个标定板上的点),我们采用和2D点归一化类似的方法,计算有一个相似变换U(由平移和缩放组成),将所有3D点Xw变为X'=UXw,达到如下目的
变换后所有3D点的中心的坐标为(0, 0, 0)T
变换后所有3D点到(0, 0, 0)T的平均距离为\sqrt(3)
情况2:另外一种情况,一些3D点离相机较近,而一些点在很远处(例如拍摄远处的地平线),此时上面的归一化方法不再适用。由于我们这次重点讲相机的几何标定方法,采用的3D点都是近处的标定板上的点,因此我们忽略这部分情况,仅关注情况1.
第3步:DLT算法求解
接下来我们利用点对(X', x')来执行1.2节所述的DLT算法,求得相机矩阵P'
第4步:对结果进行反变换
最后,我们对P'应用反变换,求得真正的相机矩阵P= T-1P'U。这样算出来的相机矩阵,就是利用直接线性变换最小化代数误差时能得到的最优解
1.5 分解相机矩阵
仅仅获取相机矩阵还不够,我们还想知道相机的内参数和外参数。

首先,我们来求相机的光心c,根据定义有:

光心c的求解就很直接了,直接对P进行SVD分解P=U∑VT,那么V中对应着最小奇异值的那一列就是光心c的坐标。
接着我们来求内参矩阵和外参矩阵,对P进行变换有:
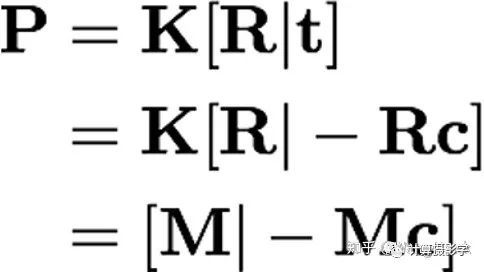
也就是说我们令
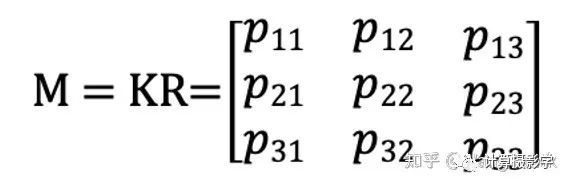
然后对M利用一个叫做RQ分解的技术进行分解,可以得到一个上三角矩阵K(要求上三角元素为正),和一个正交矩阵R, 进而可以得到t = -Rc
1.6 对已知3D-2D点对的要求
如果所有的3D点都在一个平面上,或者它们都在一条过光心的直线上,那么此时是无法唯一确定相机矩阵的。因此一般来说,会通过立体标定板来规避这种情况,1.7节就会描述这一点。
1.7 实施方案及小结
本节我们介绍了直接线性变换法DLT, 它通过已知的3D<->2D点对来求得相机矩阵,进一步分解得到相机的内参数K和外参数R、t。如何获取3D-2D点对信息呢?这里所需的点对一般是通过拍摄类似下图一样的标定板,用某种方式获取精确的3D点位置和对应的成像点位置,进而进行计算。

关于DLT,有几个点要强调
需要3D标定物,如上图的3D标定板。
需要非常精确的标定板的几何信息
非常非常准确的测量3D点和2D成像点的匹配关系
这个方法的优缺点我罗列如下:
优点
- 模型和公式简单
- 可以得到解析解
缺点
- 没有考虑到镜头畸变
- 无法引入更多约束条件。比如,实现知道了焦距信息,无法融入DLT算法进行优化
- 最关键的是,代数距离并不是计算相机矩阵的最佳距离函数!
下面这一节,我将介绍非线性求解方法,它能够避免DLT的上述缺点,得到更优的相机矩阵。
二. 非线性求解方法
非线性求解方法的关键要点如下:
将包括镜头畸变系数、内参矩阵、外参矩阵等所有信息都当做待求解的参数
定义一个比代数距离更好的距离函数
通过迭代式的非线性最优化算法,最优化上述距离函数,从而求解出待解参数
现在我们先来看看距离函数。
2.1 几何距离 vs 代数距离
1.2节介绍的代数距离为||Ap||。在《计算机视觉中的多视角几何》的第7.2节中,用一个插图来说明了这个距离的几何意义。你可以看见,代数距离实际上优化的是已知的3D点X和2D点xi的反投影点Xi'之间的距离。这并不是一个最优的距离函数。
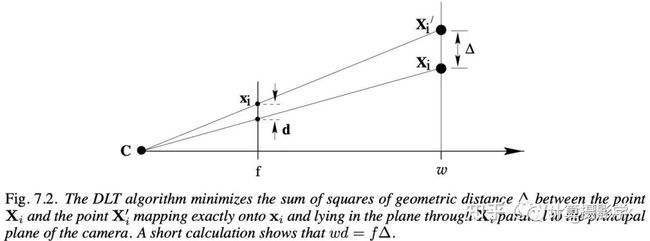
下面我们来看看几何误差(或叫几何距离),这里假设3D点的位置是准确的(比如我们有一个实现制作的非常精确的标定板),如下图所示。那么几何距离就是3D点Xi通过投影矩阵投影的2D点xi'和实际成像的2D点xi之间的距离(下图中的红线段)
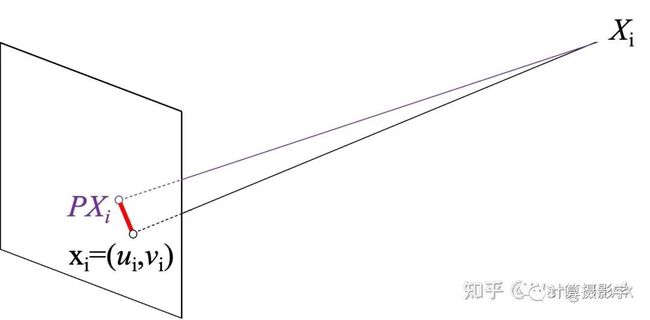
用公式表达即为:
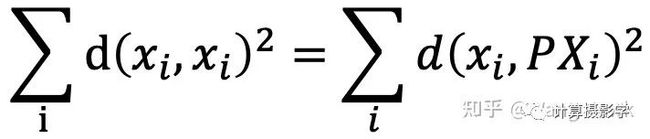
那么,整个优化过程就变成了最小化这个距离的过程
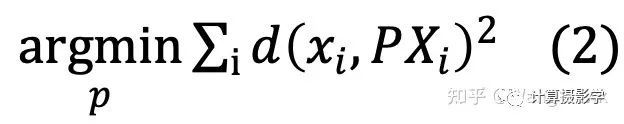
有很多优秀的软件包可用用于进行上式(2)的非线性优化。比如Minpack包里面实现的Levenberg-Marquardt 算法就是一个很出名的非线性优化算法,被很多著名的标定算法实现所采用。
2.2 考虑畸变的影响
在前面的推导中,我们一直认为三维点经过旋转、平移、缩放、错切等等齐次坐标下的线性变换就能投影为对应的二维图像点。
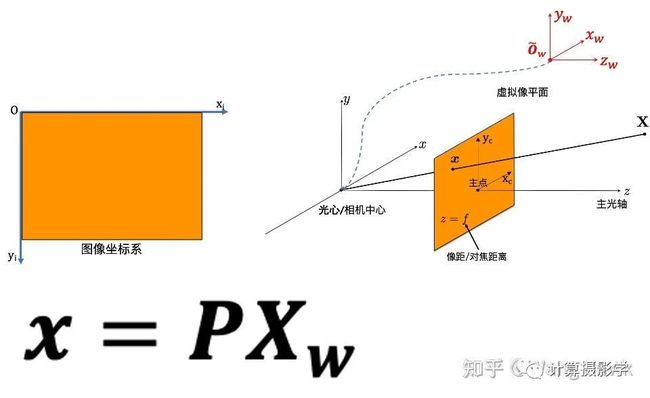
然而,正如我在文章手机中的计算摄影4-超广角畸变校正中所描述的,实际成像时镜头畸变会使得成像点产生偏移:
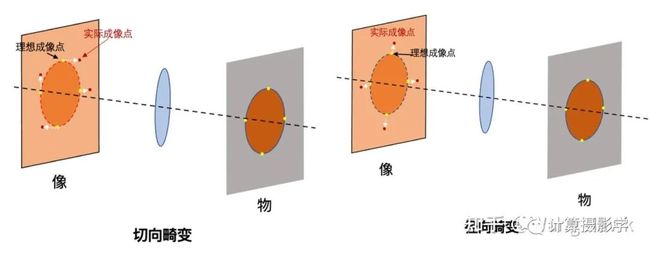
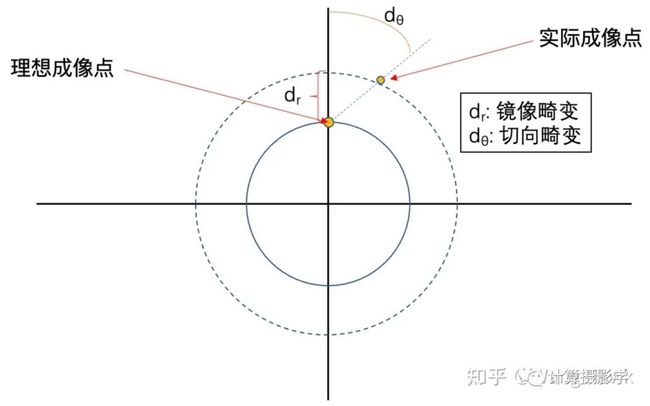

这样,前面的模型就不再适用了,如何解决这个问题呢?好在我们已经知道实际投影点和校正后的投影点之间的几何关系,因此就可以把畸变参数也带入到上面的最优化过程中,非线性最优化的魅力也在于此:
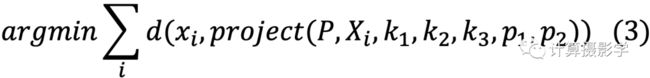
为了执行这个最优化的过程,需要给相机矩阵及畸变参数初始值。其中P的初始值可以用第一节所讲述的DLT算法得到。而畸变参数的初值可以先设置为0。
2.3 著名的实现和完整的过程
在相机几何标定的各种算法中,最出名的无疑是张正友博士发明的“张氏标定法”,这个算法在整个业界得到了广泛的应用,它最大的特点就是灵活、鲁棒、低成本。整个标定过程只需要用相机在不同的方向拍摄平面标定板(最少两次),而它实际上的核心思想就是我上面描述的非线性优化求解方法。

在Matlab和OpenCV中都有张氏标定法的实现,具体使用时先准备好一个足够平整的棋盘格标定板,然后通过不同的方向对标定板进行拍摄,然后进行计算。不需要提前知道相机和标定板之间的具体位姿关系,每次拍摄时的相机和标定板的位姿变换也是独立的,整个使用过程非常友好。

在Matlab中,把上面这些图像输入算法,算法会自动检测出棋盘格角点,并利用前面说的方法优化出各项参数,如果某幅图的平均投影误差超出了用户设置的阈值,还可以方便的过滤掉这幅图来重新进行优化计算。甚至还可以可视化每次拍摄时相机和标定板的位姿,非常方便。
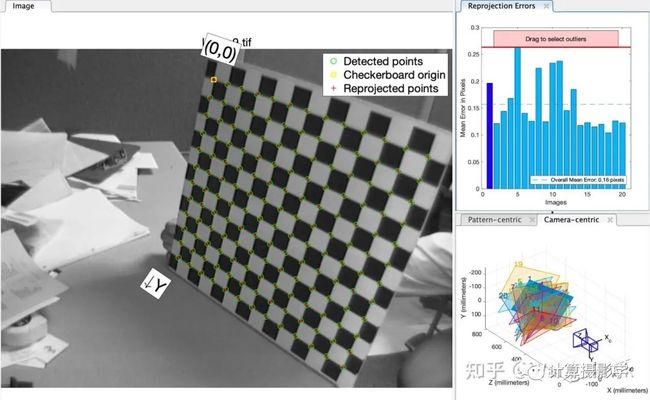
下面我补充一些张氏标定法的关键要点。
要点1:引入新的约束条件,从而可以采用平面标定板替代立体标定板
在第一节中,我讲过标定板需要是立体的,否则无法唯一确定相机矩阵。然而,立体的标定板是较难去制作的,张氏标定法追求的是低成本的标定方式,因此采用了多次拍摄平面标定板的方式来执行标定。而正因为是多次拍摄,所以每次拍摄时相机矩阵都是变化的,之前讲解的约束条件不再适用:

因此,张氏标定法重新寻求了新的约束条件,用于对内参矩阵进行约束,进而进行求解。作者观察到平面板上的点和对应的像点之间可以用一个单应矩阵H关联在一起,而且只要平面板上的角点足够多(单应矩阵有8个自由度,一对点提供2个约束,所以理论上超过4个即可),就可以求出这个单应矩阵,求解方法类似于第一节所介绍的DLT方法。
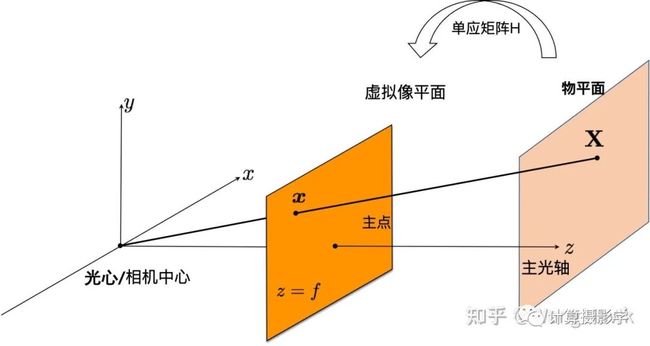
接下来,作者将单应矩阵表达为
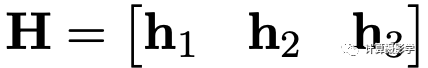
并观察到内参矩阵K和这个单应矩阵之间存在着一对约束关系:
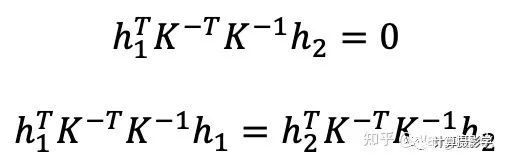
对这对约束关系进行一些变换,可以得到下面的表达式:

这样,我们又可以用SVQ分解的方式,求得b,进而求得K的各个元素。当求得了K之后,就很容易得到这一次拍摄时的外参信息(旋转R和平移t)了。上面讲的方法用于初始化内参矩阵K和每次拍摄的外参R和t,我们假设一共进行n次拍摄,每次拍摄可以获得m个成像点,那么就可以利用第一节所描述的非线性最优化方法,来最优化待解参数了。具体表达式如下:
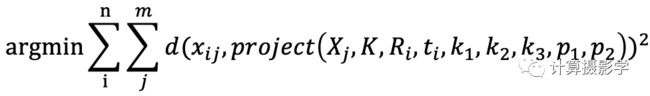
要点2:在多次拍摄时,需要改变标定板的方向
在张博士的论文中详述了如果两次拍摄时的标定板是平行的,那么实际上并没有提供额外的信息,也因此无法求解出需要的参数。
要点3:最少需要拍摄几幅图?
前面讲到,每一幅拍摄的标定板图像提供了2个对内参矩阵K的约束,而我们内参矩阵K一共有5个未知参数,所以理论上至少需要拍摄3幅图像,才能求得K:

如果我们认为s=0,即传感器像素是规整方形的,那么内参矩阵就只有4个未知参数了,这样就只需要拍摄两幅图像就能进行标定了。
前面讲过,这样的约束关系是为了求得比较好初始化内参矩阵K的。如果你能够事先知道K中元素的大概值,比如你认为s=0, 主点位于图像的中心, 而焦距又是已知的,那么理论上你只需要拍摄一幅平面的标定板一次,就可以通过非线性最小二乘法标定出相机的内外参数。
三. 总结
我在本文中讲解了相机标定的两大类方法:线性求解方法,以及非线性求解方法。
线性求解方法通过最优化代数距离来求解相机参数,它的思想和公式都比较简单,也能得到较为合理的相机参数,通常是进行非线性最优化求解的初始化方法。但它需要拍摄3D的标定物,并且需要非常准确的3D-2D对应关系,才能得到好的结果。
非线性求解方法,尤其是其中的经典方法“张氏标定法”,通过非线性最优化的方式来求解相机参数。张氏标定法追求的是灵活、鲁棒、低成本,因此用多次拍摄平面标定板来代替其他方案中拍摄3D标定物的要求。为了做到这一点,张氏标定法挖掘了新的约束关系,使得最少仅需要2张图像就可以进行相机参数的标定。
不管是哪种方法,我都提到了数据归一化的重要性,因为在求解过程中的矩阵元素如果不经过归一化,值差异较大,很容易放大数值误差,读者要特别注意这点。
总而言之,经过相机的标定,我们获得了包括畸变参数在内的相机内参,以及每次拍摄时的外参。一个很自然的问题是,如果已知相机参数,以及图像上的点,如何确定它的物点呢?在下一篇文章中,我会聊聊两视图几何的知识,敬请期待。
四. 参考资料
CMU 2021 Fall Computational Photography Course 15-463, Lecture 16
Richard Szeliski, Computer Vision: Algorithms and Application.
Richard Hartley and Andrew Zisserman, Multiple View Geometry in Computer Vision, 2nd Edition
闫令琪, GAMES101:现代计算机图形学入门
本文仅做学术分享,如有侵权,请联系删除。
重磅!计算机视觉工坊-学习交流群已成立
扫码添加小助手微信,可申请加入3D视觉工坊-学术论文写作与投稿 微信交流群,旨在交流顶会、顶刊、SCI、EI等写作与投稿事宜。
同时也可申请加入我们的细分方向交流群,目前主要有ORB-SLAM系列源码学习、3D视觉、CV&深度学习、SLAM、三维重建、点云后处理、自动驾驶、CV入门、三维测量、VR/AR、3D人脸识别、医疗影像、缺陷检测、行人重识别、目标跟踪、视觉产品落地、视觉竞赛、车牌识别、硬件选型、深度估计、学术交流、求职交流等微信群,请扫描下面微信号加群,备注:”研究方向+学校/公司+昵称“,例如:”3D视觉 + 上海交大 + 静静“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进去相关微信群。原创投稿也请联系。
▲长按加微信群或投稿
▲长按关注公众号
3D视觉从入门到精通知识星球:针对3D视觉领域的视频课程(三维重建系列、三维点云系列、结构光系列、手眼标定、相机标定、激光/视觉SLAM、自动驾驶等)、知识点汇总、入门进阶学习路线、最新paper分享、疑问解答五个方面进行深耕,更有各类大厂的算法工程人员进行技术指导。与此同时,星球将联合知名企业发布3D视觉相关算法开发岗位以及项目对接信息,打造成集技术与就业为一体的铁杆粉丝聚集区,近4000星球成员为创造更好的AI世界共同进步,知识星球入口:
学习3D视觉核心技术,扫描查看介绍,3天内无条件退款
圈里有高质量教程资料、可答疑解惑、助你高效解决问题



