深度学习课程-assign2-CNN作业与理解

知识点理解

知识点部分参考网上资料来源 - 他们解释的简单易懂，生动形象。
https://zhuanlan.zhihu.com/p/42559190
https://www.shuzhiduo.com/A/A7zge6ek54/

还有官网CNN的介绍：
https://adeshpande3.github.io/adeshpande3.github.io/A-Beginner%27s-Guide-To-Understanding-Convolutional-Neural-Networks/

图片与滤波器filters的理解

滤波器filters其实是用来检测图像中特定的特征的。filters矩阵与图片局部矩阵相对应值相乘再相加。

卷积是指用filter矩阵来覆盖着图片 相同的矩阵大小，然后对应相乘再相加得到一个数。接着，filter向左移动一个步长 stride，步长一般设置为1. 如果图片形状是（28，28），filter矩阵为（3，3），则得到的数矩阵为（26，26）。这就是卷积，卷积后的矩阵能偶够反应图片的深浅界限等特征。而CNN就是通过一个个的filter，不断地提取特征，从局部的特征到总体的特征，从而进行图像识别等等功能。

那么怎么收filter滤波器可以用来提取特征呢，举一个老鼠的例子。
我们知道一个curve detector作为一个滤波器，如下所示：

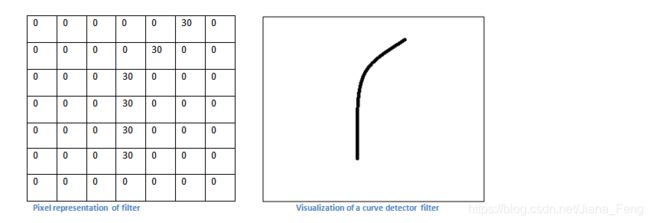
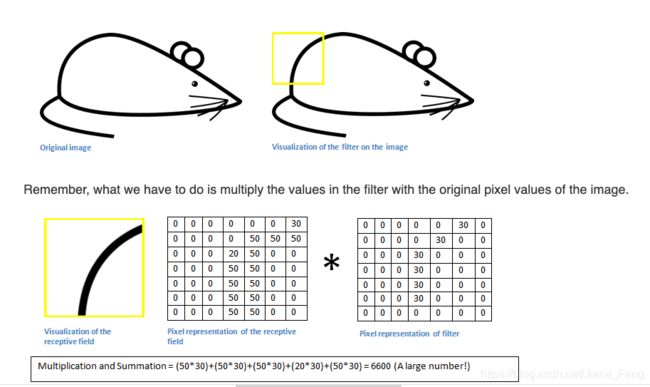
如果我们现在是要处理一张老鼠的图片。那么老鼠图片里面如果有跟我们选取的curve 滤波器矩阵相似的话，那么他们相乘之后 得到的数字就会很大。如下图所示：

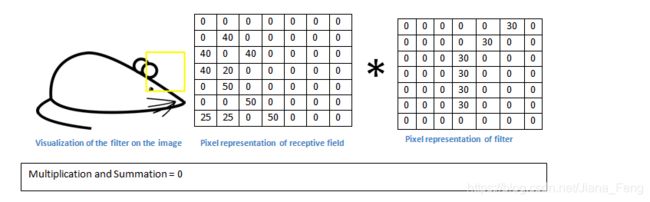
如果是curve 滤波器跟老鼠局部不一样的话，那么相乘之后就会得到一个很小的值。如下图所示：

所以，滤波器能够学习到图片里的特征，因此通常情况下，会选择多个滤波器，来学习多个特征。

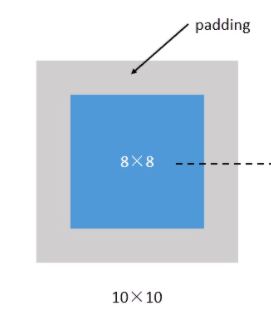
第二个名词是padding。padding是在图片上填上空白的地方。这是因为一张图片经过filter之后，得到的结果矩阵会越来越小。这就会导致图片很快就没了。其次数字的缺失会导致特征信息的遗失。因此，才会有padding填充空白，在原来图片上填充空白，比如图片大小为8✖️ 8.填充后变成10✖️ 10. 经过filter，得到的结果矩阵是 8 ✖️ 8 。 这样就维持了图片的大小。示例如下。

我们把上面这种“让卷积之后的大小不变”的padding方式，称为 “Same”方式， 把不经过任何填白的，称为 “Valid”方式。在构建网络时需要注名。

第三个名次是pooling，池化。池化的作用是提取一定区域的主要特征。减少参数数量。MaxPooling是取这个区域的最大值。AvgPooling是取这个区域的平均值。具体例子如下，采取2✖️ 2的窗口，stride步长为2.

多通道的图片处理

一般来说，图片有三种色彩通道RGB，所以图片的形状一般是(28,28,3)。 后面的3就是色彩通道。那么这时候，应该怎么filter呢？ 这时候的filter矩阵会变成(3,3,3).对应着图片的3个通道。所以，按照前面说的对应相乘然后相加。这时候相加的有27个数。前面例子相加的只有3✖️ 3 = 9个数。我们一般会称为in_channel = 3. 这时有一点要注意的是，虽然新增来一个in_channel 但是过滤后得到的结构矩阵还是原来的形状 (26,26)。

同时，还有一个名词是num_filter，也就是有时候会有多个filter来同时过滤。比如有四个filter，这时num_filter = 4. 所以事实上，filter形状为(28,28,3,4). 分别代表着 长度，宽度，色彩通道，filter个数。 这里值得注意的一点是，加多了num_filter后，过滤后的结果矩阵形状是(26,26,4) 而不是 (26,26)。

所以CNN的结构是由三层layers组成的：

1. 卷积层–Conv–filter和激活函数组成
2. 池化层–Pooling
3. 全连接层 – Fully connected --FC

手写结构便是
data–>Conv–>relu–>MaxPool/AvgPool–>Conv–>relu–>FC–>relu–>FC–>softmax–>predict/classify

【PS：值得注意的一点是 filter矩阵里面所有的数字都相当于参数，相当于传统NN里面的W参数，这些参数可以通过大量的数据学习到最优参数。】

英文专有名词定义–应付期末考试

1. Convolution: element-wise multiplication followed by summation of your input and one of your filters in the CNN context
2. Training: One thing to remember is that there would be a lot of filtersfor each layer in a CNN. (一般情况，每一层都会有很多filters来提取多个特征-每个filter提取一个特定的特征，像上面说的，一个curve filter提取一个相似的curve局部图片)。 The goal of training is to find the best filters for your task.
   typically, in the first convolutional layer which directly looks at your input, the filters try to capture information about color and edges which we know as local features。
   in higher layers, due to the effect of max-pooling, the receptive-fields of filters becomes large so more global and complex features can be detected.
   【所以是一开始的前几层layers，提取的是局部特征比如颜色，边缘这些特征。而后面的layers，由于maxpool的影响，感受野越大，其表示其能接触到的原始图像范围就越大，也意味着它可能蕴含更为全局，语义层次更高的特征】那么什么是感受野？如何计算这个感受野？
3. receptive field（感受野）：是一个神经元对原始图像的连接，指这个像素到原始图像的映射关系。具体例子解析如下 。

假设原始图片为10✖️ 10， kernel size为 3✖️ 3. 步长都是1。 共有五层网络，四层为卷积层，最后一层为Maxpooling（2✖️ 2 ）

（1）我们可以知道第一层输出网络的结果是8✖️ 8. 很明显，输出网络中的每一个像素受到原始图像的3x3区域内的影响，因为是3✖️ 3矩阵得到的一个像素，所以，输出网络中的每一个像素可以对应着原始图片的3✖️ 3区域。所以感受野是3（这个区域的大小） – RF1=3

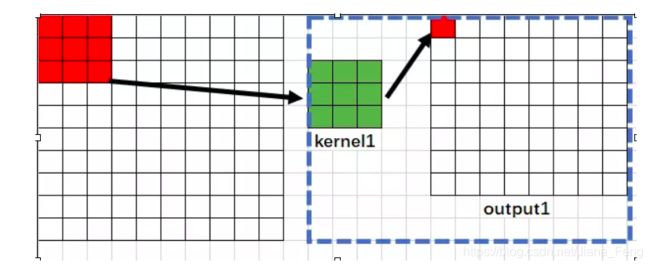
（2）第二层的输出网络是 6✖️ 6。这次网络的每一个像素，对应着上一层的3✖️ 3 区域。然后这上一层的 3✖️ 3 区域，对应着 原始图片的 5 ✖️ 5区域。具体推理如下：

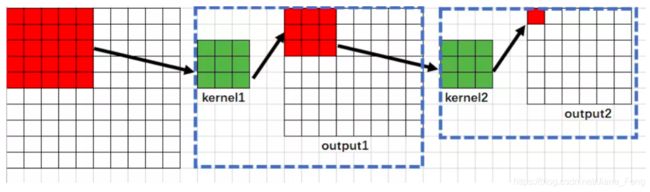
所以是，这次的每一个像素对应着原始图片的5✖️ 5区域。所以感受野为5 – RF2=5
（3）第三层输出网络是4✖️ 4，这次的网络中的每一个像素，对应着上一层的3✖️ 3区域，而上一层的 3 ✖️ 3区域对应着，上上层的5✖️ 5区域。而上上层的5✖️ 5区域对应着原始图片的7✖️ 7区域。所以这次的网络的每一个像素对应着原始图片的7✖️ 7区域，所以感受野是7，所以 RF3= 7

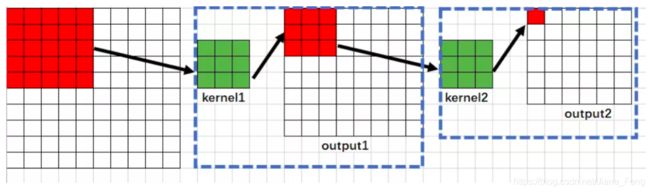
（4）第四层网络的输出是2✖️ 2，同理，这次网络的每一个像素，对应着上一层的3✖️ 3. 而上一层的3✖️ 3区域，对应着 上上层的 5✖️ 5区域，而 上上层的 5✖️ 5 区域对应着上上上层的 7 ✖️ 7区域。而上上上层 7✖️ 7区域 对应着原始图片的 9✖️ 9区域。所以这次 RF4 = 9

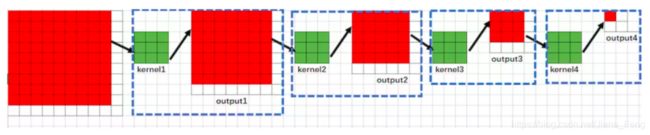
（5）最后一层是池化，把第四层的2✖️ 2变成 1✖️ 1区域。所以这一层输出的是 1✖️ 1. 对应着上一层的2 ✖️ 2。 2✖️ 2 区域对应着 第三层的 4✖️ 4区域，第三层的4✖️ 4 区域对应着第二层的 6✖️ 6区域。而第二层的6 ✖️ 6 对应着 第一层的 8✖️ 8区域，而第一层的 8✖️ 8对应着输入图片的 10✖️ 10区域。所以 这次感受野 RF5 = 10.

RF1 = 3 = k1_size [第一层的感受野，永远等于第一个卷积核的尺寸大小]
RF2 = 5 = RF1 + (k2_size - 1) ✖️ 1= 3 +（3-1）= 5
RF3 = 7 = RF2 + (k3_size - 1)✖️ 1 = 5 + （3-1）=7
RF4 = 9 = RF3 + (k4_size - 1)✖️ 1 = 7 + （3-1） = 9
RF5 = RF3 + (k5_size -1)✖️ 1 = 9 + （2-1）= 10

所以总结公式是
$k_{n}size$是表示第几层卷积层filter的大小， $R{F}_n$表示第几层的感受野 $strid{e}_n$表示第几层的步长
$$R{F}_n=R{F}_{n-1}+(k_{n}size-1)\ast strid{e}_n$$

4. Architecture: For classification tasks, a CNN usually starts with convolution followed by max-pooling. After that, the feature maps will be flattened so that we could append fully connected layers. Common activation functions include ReLu, ELU in the convolution layers, and softmax in the fully connected layers。
5. Filter/kernel/weights: a grid or a set of grids typically smaller than your input size that moves over the input space to generate output. Each filter captures one type of feature.
6. Feature/feature maps: the output of a hidden layer. Think of it as another representation of your data
7. Pooling: an downsampling operation that joins local information together, so the higher layers’ receptive fields can be bigger. The most seen pooling operation is max-pooling, which outputs the maximum of all values inside the pool.
8. Flatten: a junction between convolution layers and fully connected layers
9. Border mode: usually refers to ‘VALID’ or ‘SAME’. Under ‘VALID’ mode, only when the filter and the input fully overlap can a convolution be conducted; under ‘SAME’ mode, the output size is the same as the input size (only when the stride is 1)
   意思是under valid mode，filter是在input图片里面移动。没有padding。 而under same mode，将会有padding填充，卷积之后输出的feature map尺寸保持不变(相对于输入图片)

代码实践–下面结合CNN的作业题来理解

Task 3: Convolutional Neural Network (CNN)

虽然用tensorflow直接使用cnn函数会很容易，直接用tf.nn.conv()。但为了更好的理解CNN的每一层结构。我们将会用numpy手写每一层layer。先不包括backprop的numpy手写（之后有时间再补充）

手写Conv2d的 layer using numpy

首先，先定义Conv2d的函数
先理解一些内置函数的定义，比如使用的填充函数np.pad()

#对一维度的填充
arr1D = np.array([1, 1, 2, 2, 3, 4])
np.pad(arr1D, (2, 3), 'constant') #前面放两个0，后面放三个0 

[0, 0,1, 1, 2, 2, 3, 4, 0, 0, 0]

#对多维度的填充-3,4,4,--3是外围表示有3个 4✖️4矩阵
arr3D = np.array([[[1, 1, 2, 2], [1, 1, 2, 2], [1, 1, 2, 2],[1, 1, 2, 2]],
 				[[5, 1, 2, 6], [5, 1, 2, 6], [5, 1, 2, 6], [5, 1, 2, 6]],
  				[[1, 1, 2, 2], [1, 1, 2, 2], [1, 1, 2, 2], [1, 1, 2, 2]]]) 
#arr3D的shape是 3*4*4 3个4*4的矩阵
np.pad(arr3D, ((1, 1), (2, 2), (2, 2)), 'constant') 
#（1，1）意思是在3D数据前后加一个维度都是0，则3变成5。
#（2，2）意思是在矩阵上下加两个长度的值都为0
#（2，2）意思是在矩阵左右加两个长度的值都为0
#最后的形状为 5，8，8

回到我们的函数对于X的填充

#设置x的值
x_shape = (2, 5, 5, 3) #(batch, height, width, channels) 
#有两个batch 每个batch有5个 5*3的矩阵 
x = np.linspace(-0.1, 0.5, num=np.prod(x_shape)).reshape(x_shape)
#num=np.prod(x_shape)将会返回所有数字的乘积，这里是2*5*5*3 = 240
#开始填充x 这是pad填充选择为1 
pad = 1 
x_pad = np.pad(x, ((0, 0), (pad, pad), (pad, pad), (0, 0)), 'constant', constant_values=(0, 0))

第一个参数（0，0）表示batch不用填充，第二个参数（1，1）表示要对5个矩阵前后各自填充一个空白矩阵。所以我们将会有7个矩阵，矩阵个数表示height；第三个参数（1，1）表示对矩阵上下填充1个行0.这时矩阵上下表示width；第四个参数（0，0）表示对每个矩阵左右不用填充。这时矩阵宽度表示channels 不用填充。
所以填充之后，形状是2，7，7，3

def conv2d_forward(x, w, b, pad, stride):
	‘’‘
	Inputs:
	:param x: Input data. Should have size (batch, height, width, channels-一般是RGB通道3)
	:param w: Filter. Should have size (filter_height, filter_width, channels, num_of_filters)
	:param b: Bias term. Should have size (num_of_filters, )
	:param pad填充: Integer. The number of zeroes to pad along the height and width axis
	:param stride步长: Integer. The number of pixels to move between 2 neighboring receptive fields
	
	:return: A 4-D array. Should have size (batch, new_height, new_width, num_of_filters)

	这里值得注意的是 经过filter之后的矩阵大小计算是 
	new_height = ((height - filter_height + 2 * pad) // stride) + 1
	【比如8✖️8矩阵 经过 filter 3✖️3 先不算上填充pad，步长为 1， 得到的矩阵是((8-3)+1)=6】
	
    new_width = ((width - filter_width + 2 * pad) // stride) + 1
    
	’‘‘
	#我自己习惯把RGB通道称为in_channel , num_filters 称为 out_channel
	batch_size, height, width, in_channel = x.shape
	filter_height,filter_width, out_channel = w.shape[0],w.shape[1],w.shape[3]
	#计算filter后的shape
	new_height = ((height - filter_height + 2 * pad) // stride) + 1
	new_width = ((width - filter_width + 2 * pad) // stride) + 1
	#填充x,填充后形状变成 2,7,7,3 
	x_pad = np.pad(x, ((0, 0), (pad, pad), (pad, pad), (0, 0)), 'constant', constant_values=(0, 0))
	#set好output的形状
	out = np.zeros([batch_size,new_height,new_width,out_channel])
	
	#开始卷积计算 
	for batch in range(batch_size):
		for nh in range(new_height):
			for nw in range(new_width):
				for out_c in range(out_channel):
					out[batch,nh,nw,out_c] = np.sum(x_pad[batch,nh * stride : nh * stride + filter_height,nw * stride : nw * stride + filter_width,:] * w[:,:,:,out_c]) + b[out_c]
	return out 

设置数据来检查

x_shape = (2, 5, 5, 3) #(batch, height, width, channels)
w_shape = (3, 3, 3, 5) #(filter_height, filter_width, channels, num_of_filters)
channels = w_shape[-1]

x = np.linspace(-0.1, 0.5, num=np.prod(x_shape)).reshape(x_shape)
w = np.linspace(-0.2, 0.3, num=np.prod(w_shape)).reshape(w_shape)
b = np.linspace(-0.1, 0.2, num=channels)
pad = 1
stride = 2
your_feedforward = conv2d_forward(x, w, b, pad, stride)

print("Your feedforward result (size :{}) is: ".format(your_feedforward.shape))
print(your_feedforward)

跟tf出来的效果对比

X_tf = tf.constant(x, shape=x_shape)
w_tf = tf.constant(w, shape=w_shape)
b_tf = tf.constant(b, shape=channels)

def conv2d_forward_2(x, w, b, stride):
    # stride in tf.nn.conv2d is in the format: [1, x_movement, y_movement, 1]
    feedforward = tf.nn.conv2d(x, w, [1, stride, stride, 1], padding = "SAME")
    # add bias to the conv network
    feedforward = tf.nn.bias_add(feedforward, b)
    return feedforward
print("Is your feedforward correct? {}".format(np.allclose(your_feedforward, conv2d_forward_2(X_tf, w_tf, b_tf, stride))))

Maxpooling using numpy

def max_pool_forward(x, pool_size, stride):
	‘’‘
	Inputs:
	:params x: Input data. Should have size (batch, height, width, channels).
		
	:return :A 4-D array. Should have size (batch, new_height, new_width, num_of_filters)
	’‘’
	batch_size, height, width, channels = x.shape
	#得到新的矩阵大小
	new_height = ((height - pool_size) // stride) + 1
	new_width = ((width - pool_size) // stride) + 1
	#设置output形状
	out = np.zeros((batch_size, new_height, new_width, channels))
	
	#直接圈出区域 最后直接取最大值。
	for batch in range(batch_size):
		for nh in range(new_height):
			for nw in range(new_width):
				for c in range(channels):
					out[batch,nh,nw,c] = np.max(
					x[batch,nh*stride:nh*stride+pool_size, nw*stride:nw*stride+pool_size,c]
					)
	return out 

检查数据

x_shape = (2, 5, 5, 3) #(batch, height, width, channels)
x = np.linspace(-0.5, 0.5, num=np.prod(x_shape)).reshape(x_shape)
pool_size = 2
stride = 2

your_feedforward = max_pool_forward(x, pool_size, stride)

print("Your feedforward result (size :{}) is: ".format(your_feedforward.shape))

对比tf出来的值

X_tf = tf.constant(x, shape=x_shape)

def maxpool_forward_2(x, pool_size, stride):
    maxpool_forward = tf.nn.max_pool(x, [1, pool_size, pool_size, 1], [1, stride, stride, 1], padding='VALID')
    return maxpool_forward

## Print validation result
print("Is your feedforward correct? {}".format(np.allclose(your_feedforward, maxpool_forward_2(X_tf, pool_size, stride))))

Is your feedforward correct? True

好的，关于深度学习课程的cnn模型以及作业理解到此为止。