深度学习+pytorch自学笔记（十）——含并行连结的网络（GoogLeNet）、批量归一化、残差网络（ResNet）、稠密连接网络（DenseNet）

参考书籍《动手学深度学习(pytorch版），参考网址为：

https://tangshusen.me/Dive-into-DL-PyTorch/#/chapter05_CNN/5.9_googlenet

https://zh-v2.d2l.ai/chapter_convolutional-modern/googlenet.html

请大家也多多支持这两个很好用的平台~

大部分内容为书中内容，也有部分自己实验和添加的内容，如涉及侵权，会进行删除。

一、含并行连结的网络（GoogLeNet）

1.1 Inception 块

GoogLeNet中的基础卷积块叫作Inception块，得名于同名电影《盗梦空间》（Inception）。与上一节介绍的NiN块相比，这个基础块在结构上更加复杂，如图所示。

由图5.8可以看出，Inception块里有4条并行的线路。前3条线路使用窗口大小分别是1×1、3×3和5×5的卷积层来抽取不同空间尺寸下的信息，其中中间2个线路会对输入先做1×1卷积来减少输入通道数，以降低模型复杂度。第四条线路则使用3×3最大池化层，后接1×1卷积层来改变通道数。4条线路都使用了合适的填充来使输入与输出的高和宽一致。最后我们将每条线路的输出在通道维上连结，并输入接下来的层中去。

Inception块中可以自定义的超参数是每个层的输出通道数，我们以此来控制模型复杂度。

1.2 GoogLeNet模型

GoogLeNet跟VGG一样，在主体卷积部分中使用5个模块（block），每个模块之间使用步幅为2的3×3最大池化层来减小输出高宽。第一模块使用一个64通道的7×7卷积层。

第二模块使用2个卷积层：首先是64通道的1×1卷积层，然后是将通道增大3倍的3×3卷积层。它对应Inception块中的第二条线路。

第三模块串联2个完整的Inception块。第一个Inception块的输出通道数为64+128+32+32=256，其中4条线路的输出通道数比例为64:128:32:32=2:4:1:1。其中第二、第三条线路先分别将输入通道数减小至96/192=1/2和16/192=1/12后，再接上第二层卷积层。第二个Inception块输出通道数增至128+192+96+64=480，每条线路的输出通道数之比为128:192:96:64=4:6:3:2。其中第二、第三条线路先分别将输入通道数减小至128/256=1/2和32/256=1/8。

第四模块更加复杂。它串联了5个Inception块，其输出通道数分别是192+208+48+64=512、160+224+64+64=512、128+256+64+64=512、112+288+64+64=528和256+320+128+128=832。这些线路的通道数分配和第三模块中的类似，首先含3×3卷积层的第二条线路输出最多通道，其次是仅含1×1卷积层的第一条线路，之后是含5×5卷积层的第三条线路和含3×3最大池化层的第四条线路。其中第二、第三条线路都会先按比例减小通道数。这些比例在各个Inception块中都略有不同。

第五模块有输出通道数为256+320+128+128=832和384+384+128+128=1024的两个Inception块。其中每条线路的通道数的分配思路和第三、第四模块中的一致，只是在具体数值上有所不同。需要注意的是，第五模块的后面紧跟输出层，该模块同NiN一样使用全局平均池化层来将每个通道的高和宽变成1。最后我们将输出变成二维数组后接上一个输出个数为标签类别数的全连接层。

GoogLeNet模型的计算复杂，而且不如VGG那样便于修改通道数。本节里我们将输入的高和宽从224降到96来简化计算。

demo1:

import torch
from torch import nn
import torch.nn.functional as F
import d2lzh_pytorch as d2l

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

class Inception(nn.Module):
    # c1 - c4为每条线路里的层的输出通道数
    def __init__(self, in_c, c1, c2, c3, c4):
        super(Inception, self).__init__()
        # 线路1，单1 x 1卷积层
        self.p1_1 = nn.Conv2d(in_c, c1, kernel_size=1)
        # 线路2，1 x 1卷积层后接3 x 3卷积层
        self.p2_1 = nn.Conv2d(in_c, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1 x 1卷积层后接5 x 5卷积层
        self.p3_1 = nn.Conv2d(in_c, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3 x 3最大池化层后接1 x 1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_c, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))  # 池化层后不接激活函数
        return torch.cat((p1, p2, p3, p4), dim=1)  # 在通道维上连结输出

# GoogLeNet模型
# 第一模块
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

# 第二模块
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

# 第三模块
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

# 第四模块
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

# 第五模块
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   d2l.GlobalAvgPool2d())

net = nn.Sequential(b1, b2, b3, b4, b5,
                    d2l.FlattenLayer(), nn.Linear(1024, 10))

# 演示各个模块之间的输出的形状变化
X = torch.rand(1, 1, 96, 96)
for blk in net.children():
    X = blk(X)
    print('output shape: ', X.shape)

# 获取数据和训练模型
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)

lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)

out1:

output shape:  torch.Size([1, 64, 24, 24])
output shape:  torch.Size([1, 192, 12, 12])
output shape:  torch.Size([1, 480, 6, 6])
output shape:  torch.Size([1, 832, 3, 3])
output shape:  torch.Size([1, 1024, 1, 1])
output shape:  torch.Size([1, 1024])
output shape:  torch.Size([1, 10])
training on  cuda
epoch 1, loss 0.0087, train acc 0.570, test acc 0.831, time 45.5 sec
epoch 2, loss 0.0032, train acc 0.851, test acc 0.853, time 48.5 sec
epoch 3, loss 0.0026, train acc 0.880, test acc 0.883, time 45.4 sec
epoch 4, loss 0.0022, train acc 0.895, test acc 0.887, time 46.6 sec
epoch 5, loss 0.0020, train acc 0.906, test acc 0.896, time 43.5 sec

小结
1.Inception块相当于一个有4条线路的子网络。它通过不同窗口形状的卷积层和最大池化层来并行抽取信息，并使用1×1卷积层减少通道数从而降低模型复杂度。

2.GoogLeNet将多个设计精细的Inception块和其他层串联起来。其中Inception块的通道数分配之比是在ImageNet数据集上通过大量的实验得来的。

3.GoogLeNet和它的后继者们一度是ImageNet上最高效的模型之一：在类似的测试精度下，它们的计算复杂度往往更低。

二、批量归一化

本节介绍批量归一化（batch normalization）层，它能让较深的神经网络的训练变得更加容易 。在实战Kaggle比赛：预测房价里，我们对输入数据做了标准化处理：处理后的任意一个特征在数据集中所有样本上的均值为0、标准差为1。标准化处理输入数据使各个特征的分布相近：这往往更容易训练出有效的模型。

通常来说，数据标准化预处理对于浅层模型就足够有效了。随着模型训练的进行，当每层中参数更新时，靠近输出层的输出较难出现剧烈变化。但对深层神经网络来说，即使输入数据已做标准化，训练中模型参数的更新依然很容易造成靠近输出层输出的剧烈变化。这种计算数值的不稳定性通常令我们难以训练出有效的深度模型。

批量归一化的提出正是为了应对深度模型训练的挑战。在模型训练时，批量归一化利用小批量上的均值和标准差，不断调整神经网络中间输出，从而使整个神经网络在各层的中间输出的数值更稳定。批量归一化和下一节将要介绍的残差网络为训练和设计深度模型提供了两类重要思路。

2.1 批量归一化层

对全连接层和卷积层做批量归一化的方法稍有不同。下面将分别介绍这两种情况下的批量归一化。

对全连接层做批量归一化

对卷积层做批量归一化

对卷积层来说，批量归一化发生在卷积计算之后、应用激活函数之前。如果卷积计算输出多个通道，我们需要对这些通道的输出分别做批量归一化，且每个通道都拥有独立的拉伸和偏移参数，并均为标量。设小批量中有m个样本。在单个通道上，假设卷积计算输出的高和宽分别为p和q。我们需要对该通道中m×p×q个元素同时做批量归一化。对这些元素做标准化计算时，我们使用相同的均值和方差，即该通道中m×p×q个元素的均值和方差。

使用批量归一化训练时，我们可以将批量大小设得大一点，从而使批量内样本的均值和方差的计算都较为准确。将训练好的模型用于预测时，我们希望模型对于任意输入都有确定的输出。因此，单个样本的输出不应取决于批量归一化所需要的随机小批量中的均值和方差。一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差，并在预测时使用它们得到确定的输出。可见，和丢弃层一样，批量归一化层在训练模式和预测模式下的计算结果也是不一样的。

2.2 从零实现

我们自定义一个BatchNorm层。它保存参与求梯度和迭代的拉伸参数gamma和偏移参数beta，同时也维护移动平均得到的均值和方差，以便能够在模型预测时被使用。BatchNorm实例所需指定的num_features参数对于全连接层来说应为输出个数，对于卷积层来说则为输出通道数。该实例所需指定的num_dims参数对于全连接层和卷积层来说分别为2和4。

截图链接：https://zhuanlan.zhihu.com/p/337910973

demo2:

import torch
import myutils
from torch import nn
import d2lzh_pytorch as d2l

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 批量归一化层
def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 判断当前模式是训练模式还是预测模式
    if not is_training:
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)  # 各个样本之间同一种特征做平均
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。这里我们需要保持
            # X的形状以便后面可以做广播运算
            mean = X.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
            var = ((X - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
        # 训练模式下用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 拉伸和偏移
    return Y, moving_mean, moving_var

# 自定义一个BatchNorm层
class BatchNorm(nn.Module):
    def __init__(self, num_features, num_dims):
        super(BatchNorm, self).__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成0和1
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 不参与求梯度和迭代的变量，全在内存上初始化成0
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.zeros(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var, Module实例的traning属性默认为true, 调用.eval()后设成false
        Y, self.moving_mean, self.moving_var = batch_norm(self.training,
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

# 使用批量归一化层的LeNet
net = nn.Sequential(
            nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
            BatchNorm(6, num_dims=4),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2), # kernel_size, stride
            nn.Conv2d(6, 16, 5),
            BatchNorm(16, num_dims=4),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2),
            d2l.FlattenLayer(),
            nn.Linear(16*4*4, 120),
            BatchNorm(120, num_dims=2),
            nn.Sigmoid(),
            nn.Linear(120, 84),
            BatchNorm(84, num_dims=2),
            nn.Sigmoid(),
            nn.Linear(84, 10)
        )

# 训练模型
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

lr, num_epochs = 0.001, 10
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
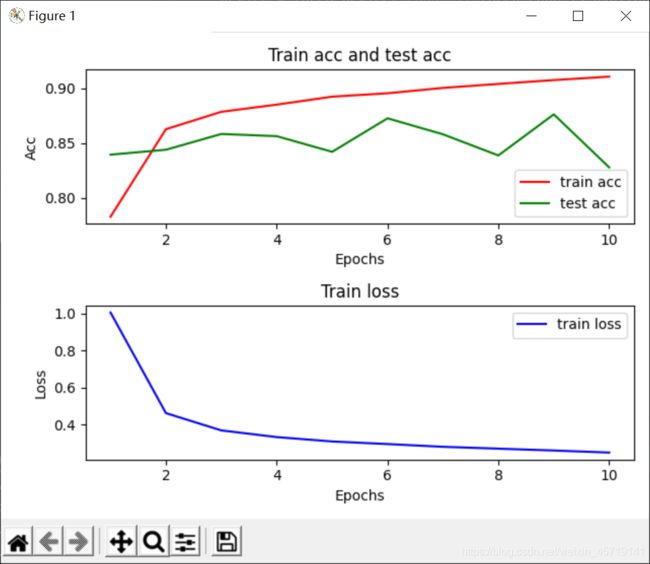
loss_list, train_acc_list, test_acc_list = myutils.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
myutils.show_img(num_epochs, loss_list, train_acc_list, test_acc_list)

# 查看参数
print(net[1].gamma.view((-1,)), net[1].beta.view((-1,)))  # net[1]表示第一个BatchNorm()

out2:

training on  cuda
epoch 1, loss 1.0086, train acc 0.778, test acc 0.800, time 7.4 sec
epoch 2, loss 0.4607, train acc 0.862, test acc 0.842, time 5.6 sec
epoch 3, loss 0.3722, train acc 0.877, test acc 0.856, time 5.7 sec
epoch 4, loss 0.3344, train acc 0.886, test acc 0.851, time 5.7 sec
epoch 5, loss 0.3117, train acc 0.891, test acc 0.871, time 5.7 sec
epoch 6, loss 0.2950, train acc 0.895, test acc 0.857, time 5.7 sec
epoch 7, loss 0.2824, train acc 0.901, test acc 0.878, time 5.7 sec
epoch 8, loss 0.2684, train acc 0.904, test acc 0.889, time 5.8 sec
epoch 9, loss 0.2608, train acc 0.907, test acc 0.870, time 5.8 sec
epoch 10, loss 0.2520, train acc 0.910, test acc 0.881, time 5.8 sec
tensor([0.9718, 1.0241, 1.1920, 1.0987, 1.0251, 1.0467], device='cuda:0',
       grad_fn=<ViewBackward>) tensor([-0.5608, -0.7507,  0.0971, -0.8572,  0.0305,  0.0637], device='cuda:0',
       grad_fn=<ViewBackward>)

简洁实现

与刚刚自己定义的BatchNorm类相比，Pytorch中nn模块定义的BatchNorm1d和BatchNorm2d类使用起来更加简单，二者分别用于全连接层和卷积层，都需要指定输入的num_features参数值。下面我们用PyTorch实现使用批量归一化的LeNet。

demo3:

import torch
import myutils
from torch import nn
import d2lzh_pytorch as d2l

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

net = nn.Sequential(
            nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
            nn.BatchNorm2d(6),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2), # kernel_size, stride
            nn.Conv2d(6, 16, 5),
            nn.BatchNorm2d(16),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2),
            d2l.FlattenLayer(),
            nn.Linear(16*4*4, 120),
            nn.BatchNorm1d(120),
            nn.Sigmoid(),
            nn.Linear(120, 84),
            nn.BatchNorm1d(84),
            nn.Sigmoid(),
            nn.Linear(84, 10)
        )

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

lr, num_epochs = 0.001, 10
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
loss_list, train_acc_list, test_acc_list = myutils.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
myutils.show_img(num_epochs, loss_list, train_acc_list, test_acc_list)

out3:

training on  cuda
epoch 1, loss 1.0057, train acc 0.783, test acc 0.840, time 6.9 sec
epoch 2, loss 0.4630, train acc 0.863, test acc 0.844, time 5.1 sec
epoch 3, loss 0.3699, train acc 0.879, test acc 0.859, time 5.2 sec
epoch 4, loss 0.3337, train acc 0.885, test acc 0.857, time 5.2 sec
epoch 5, loss 0.3102, train acc 0.893, test acc 0.842, time 5.2 sec
epoch 6, loss 0.2962, train acc 0.896, test acc 0.873, time 5.2 sec
epoch 7, loss 0.2814, train acc 0.901, test acc 0.858, time 5.2 sec
epoch 8, loss 0.2714, train acc 0.904, test acc 0.839, time 5.2 sec
epoch 9, loss 0.2615, train acc 0.908, test acc 0.876, time 5.1 sec
epoch 10, loss 0.2503, train acc 0.911, test acc 0.828, time 5.1 sec

小结

1.在模型训练时，批量归一化利用小批量上的均值和标准差，不断调整神经网络的中间输出，从而使整个神经网络在各层的中间输出的数值更稳定。
2.对全连接层和卷积层做批量归一化的方法稍有不同。
3.批量归一化层和丢弃层一样，在训练模式和预测模式的计算结果是不一样的。
4.PyTorch提供了BatchNorm类方便使用。

三、残差网络（ResNet）

让我们先思考一个问题：对神经网络模型添加新的层，充分训练后的模型是否只可能更有效地降低训练误差？理论上，原模型解的空间只是新模型解的空间的子空间。也就是说，如果我们能将新添加的层训练成恒等映射f(x)=x，新模型和原模型将同样有效。由于新模型可能得出更优的解来拟合训练数据集，因此添加层似乎更容易降低训练误差。然而在实践中，添加过多的层后训练误差往往不降反升。即使利用批量归一化带来的数值稳定性使训练深层模型更加容易，该问题仍然存在。针对这一问题，何恺明等人提出了残差网络（ResNet） [1]。它在2015年的ImageNet图像识别挑战赛夺魁，并深刻影响了后来的深度神经网络的设计。

3.1 残差块

让我们聚焦于神经网络局部。如图所示，设输入为x。假设我们希望学出的理想映射为f(x)，从而作为图上方激活函数的输入。左图虚线框中的部分需要直接拟合出该映射f(x)，而右图虚线框中的部分则需要拟合出有关恒等映射的残差映射f(x)−x。残差映射在实际中往往更容易优化。以本节开头提到的恒等映射作为我们希望学出的理想映射f(x)。我们只需将图中右图虚线框内上方的加权运算（如仿射）的权重和偏差参数学成0，那么f(x)即为恒等映射。实际中，当理想映射f(x)极接近于恒等映射时，残差映射也易于捕捉恒等映射的细微波动。图5.9右图也是ResNet的基础块，即残差块（residual block）。在残差块中，输入可通过跨层的数据线路更快地向前传播。

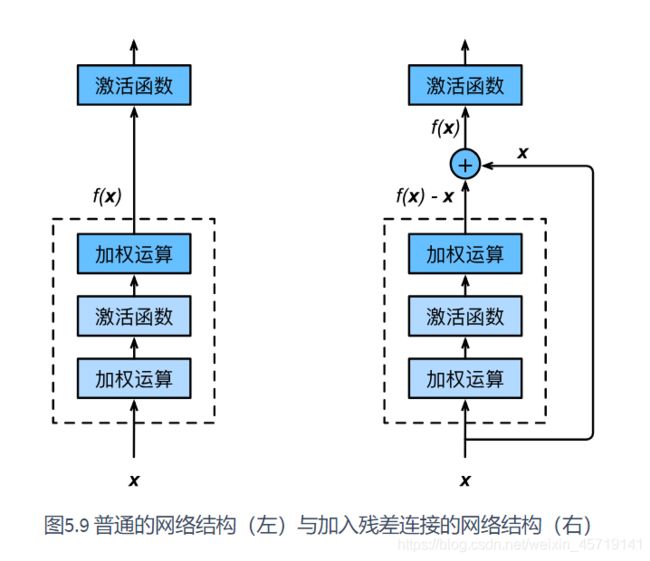
ResNet沿用了VGG全3×3卷积层的设计。残差块里首先有2个有相同输出通道数的3×3卷积层。每个卷积层后接一个批量归一化层和ReLU激活函数。然后我们将输入跳过这两个卷积运算后直接加在最后的ReLU激活函数前。这样的设计要求两个卷积层的输出与输入形状一样，从而可以相加。如果想改变通道数，就需要引入一个额外的1×1卷积层来将输入变换成需要的形状后再做相加运算。

残差块可以设定输出通道数、是否使用额外的1×1卷积层来修改通道数以及卷积层的步幅。

3.2 ResNet模型

ResNet的前两层跟之前介绍的GoogLeNet中的一样：在输出通道数为64、步幅为2的7×7卷积层后接步幅为2的3×3的最大池化层。不同之处在于ResNet每个卷积层后增加的批量归一化层。

GoogLeNet在后面接了4个由Inception块组成的模块。ResNet则使用4个由残差块组成的模块，每个模块使用若干个同样输出通道数的残差块。第一个模块的通道数同输入通道数一致。由于之前已经使用了步幅为2的最大池化层，所以无须减小高和宽。之后的每个模块在第一个残差块里将上一个模块的通道数翻倍，并将高和宽减半。

下面我们来实现这个模块。注意，这里对第一个模块做了特别处理。

接着我们为ResNet加入所有残差块。这里每个模块使用两个残差块。

最后，与GoogLeNet一样，加入全局平均池化层后接上全连接层输出。

这里每个模块里有4个卷积层（不计算1×1卷积层），加上最开始的卷积层和最后的全连接层，共计18层。这个模型通常也被称为ResNet-18。通过配置不同的通道数和模块里的残差块数可以得到不同的ResNet模型，例如更深的含152层的ResNet-152。虽然ResNet的主体架构跟GoogLeNet的类似，但ResNet结构更简单，修改也更方便。这些因素都导致了ResNet迅速被广泛使用。

demo4:

import torch
import myutils
from torch import nn
import torch.nn.functional as F
import d2lzh_pytorch as d2l

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 残差块的实现
class Residual(nn.Module):  # 本类已保存在d2lzh_pytorch包中方便以后使用
    def __init__(self, in_channels, out_channels, use_1x1conv=False, stride=1):
        super(Residual, self).__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1, stride=stride)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.bn2 = nn.BatchNorm2d(out_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        return F.relu(Y + X)

# 查看输入和输出形状
blk = Residual(3, 3)
X = torch.rand((4, 3, 6, 6))
print(blk(X).shape) # torch.Size([4, 3, 6, 6])

# 在增加输出通道数的同时减半输出的高和宽
blk = Residual(3, 6, use_1x1conv=True, stride=2)
print(blk(X).shape) # torch.Size([4, 6, 3, 3])

# ResNet模型
net = nn.Sequential(
        nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
        nn.BatchNorm2d(64),
        nn.ReLU(),
        nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

def resnet_block(in_channels, out_channels, num_residuals, first_block=False):
    if first_block:
        assert in_channels == out_channels # 第一个模块的通道数同输入通道数一致
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(in_channels, out_channels, use_1x1conv=True, stride=2))
        else:
            blk.append(Residual(out_channels, out_channels))
    return nn.Sequential(*blk)

# 为ResNet加入所有残差块。这里每个模块使用两个残差块
net.add_module("resnet_block1", resnet_block(64, 64, 2, first_block=True))
net.add_module("resnet_block2", resnet_block(64, 128, 2))
net.add_module("resnet_block3", resnet_block(128, 256, 2))
net.add_module("resnet_block4", resnet_block(256, 512, 2))

# 加入全局平均池化层后接上全连接层输出
net.add_module("global_avg_pool", d2l.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, 512, 1, 1)
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(), nn.Linear(512, 10)))

# 观察一下输入形状在ResNet不同模块之间的变化
X = torch.rand((1, 1, 224, 224))
for name, layer in net.named_children():
    X = layer(X)
    print(name, ' output shape:\t', X.shape)

# 获取数据和训练模型
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96) # 将输入的高和宽从224降到96来简化计算

lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
loss_list, train_acc_list, test_acc_list = myutils.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
myutils.show_img(num_epochs, loss_list, train_acc_list, test_acc_list)

out4:

torch.Size([4, 3, 6, 6])
torch.Size([4, 6, 3, 3])
0  output shape:	 torch.Size([1, 64, 112, 112])
1  output shape:	 torch.Size([1, 64, 112, 112])
2  output shape:	 torch.Size([1, 64, 112, 112])
3  output shape:	 torch.Size([1, 64, 56, 56])
resnet_block1  output shape:	 torch.Size([1, 64, 56, 56])
resnet_block2  output shape:	 torch.Size([1, 128, 28, 28])
resnet_block3  output shape:	 torch.Size([1, 256, 14, 14])
resnet_block4  output shape:	 torch.Size([1, 512, 7, 7])
global_avg_pool  output shape:	 torch.Size([1, 512, 1, 1])
fc  output shape:	 torch.Size([1, 10])
training on  cuda
epoch 1, loss 0.0015, train acc 0.853, test acc 0.885, time 31.0 sec
epoch 2, loss 0.0010, train acc 0.910, test acc 0.899, time 31.8 sec
epoch 3, loss 0.0008, train acc 0.926, test acc 0.911, time 31.6 sec
epoch 4, loss 0.0007, train acc 0.936, test acc 0.916, time 31.8 sec
epoch 5, loss 0.0006, train acc 0.944, test acc 0.926, time 31.5 sec

具体算法参考链接：https://zhuanlan.zhihu.com/p/42706477

小结

1.残差块通过跨层的数据通道从而能够训练出有效的深度神经网络。
2.ResNet深刻影响了后来的深度神经网络的设计。

四、稠密连接网络（DenseNet）

ResNet中的跨层连接设计引申出了数个后续工作。本节我们介绍其中的一个：稠密连接网络（DenseNet） [1]。 它与ResNet的主要区别如图5.10所示。

图5.10中将部分前后相邻的运算抽象为模块A和模块B。与ResNet的主要区别在于，DenseNet里模块B的输出不是像ResNet那样和模块A的输出相加，而是在通道维上连结。这样模块A的输出可以直接传入模块BB后面的层。在这个设计里，模块A直接跟模块BB后面的所有层连接在了一起。这也是它被称为“稠密连接”的原因。

DenseNet的主要构建模块是稠密块（dense block）和过渡层（transition layer）。前者定义了输入和输出是如何连结的，后者则用来控制通道数，使之不过大。

4.2 稠密块

DenseNet使用了ResNet改良版的“批量归一化、激活和卷积”结构，我们首先在conv_block函数里实现这个结构。

稠密块由多个conv_block组成，每块使用相同的输出通道数。但在前向计算时，我们将每块的输入和输出在通道维上连结。

定义一个有2个输出通道数为10的卷积块。使用通道数为3的输入时，我们会得到通道数为3+2×10=23的输出。卷积块的通道数控制了输出通道数相对于输入通道数的增长，因此也被称为增长率（growth rate）。

过渡层

由于每个稠密块都会带来通道数的增加，使用过多则会带来过于复杂的模型。过渡层用来控制模型复杂度。它通过1×1卷积层来减小通道数，并使用步幅为2的平均池化层减半高和宽，从而进一步降低模型复杂度。

DenseNet模型

DenseNet首先使用同ResNet一样的单卷积层和最大池化层。

类似于ResNet接下来使用的4个残差块，DenseNet使用的是4个稠密块。同ResNet一样，我们可以设置每个稠密块使用多少个卷积层。这里我们设成4，从而与上一节的ResNet-18保持一致。稠密块里的卷积层通道数（即增长率）设为32，所以每个稠密块将增加128个通道。

ResNet里通过步幅为2的残差块在每个模块之间减小高和宽。这里我们则使用过渡层来减半高和宽，并减半通道数。

同ResNet一样，最后接上全局池化层和全连接层来输出。

demo5:

import torch
from torch import nn
import d2lzh_pytorch as d2l

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# ResNet改良版的“批量归一化、激活和卷积”结构
def conv_block(in_channels, out_channels):
    blk = nn.Sequential(nn.BatchNorm2d(in_channels),
                        nn.ReLU(),
                        nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
    return blk

# 稠密块
class DenseBlock(nn.Module):
    def __init__(self, num_convs, in_channels, out_channels):
        super(DenseBlock, self).__init__()
        net = []
        for i in range(num_convs):
            in_c = in_channels + i * out_channels
            net.append(conv_block(in_c, out_channels))
        self.net = nn.ModuleList(net)
        self.out_channels = in_channels + num_convs * out_channels # 计算输出通道数

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            X = torch.cat((X, Y), dim=1)  # 在通道维上将输入和输出连结
        return X

# 定义一个有2个输出通道数为10的卷积块。使用通道数为3的输入时，我们会得到通道数为3+2×10=23的输出
blk = DenseBlock(2, 3, 10)
X = torch.rand(4, 3, 8, 8)
Y = blk(X)
print(Y.shape) # torch.Size([4, 23, 8, 8])

# 过渡层
def transition_block(in_channels, out_channels):
    blk = nn.Sequential(
            nn.BatchNorm2d(in_channels),
            nn.ReLU(),
            nn.Conv2d(in_channels, out_channels, kernel_size=1),
            nn.AvgPool2d(kernel_size=2, stride=2))
    return blk

# 对上一个例子中稠密块的输出使用通道数为10的过渡层。此时输出的通道数减为10，高和宽均减半
blk = transition_block(23, 10)
print(blk(Y).shape) # torch.Size([4, 10, 4, 4])

# DenseNet模型
net = nn.Sequential(
        nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
        nn.BatchNorm2d(64),
        nn.ReLU(),
        nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

num_channels, growth_rate = 64, 32  # num_channels为当前的通道数
num_convs_in_dense_blocks = [4, 4, 4, 4]

for i, num_convs in enumerate(num_convs_in_dense_blocks):
    DB = DenseBlock(num_convs, num_channels, growth_rate)
    net.add_module("DenseBlosk_%d" % i, DB)
    # 上一个稠密块的输出通道数
    num_channels = DB.out_channels
    # 在稠密块之间加入通道数减半的过渡层
    if i != len(num_convs_in_dense_blocks) - 1:  # 最后一个稠密块不需要过渡层
        net.add_module("transition_block_%d" % i, transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2

# 同ResNet一样，最后接上全局池化层和全连接层来输出
net.add_module("BN", nn.BatchNorm2d(num_channels))
net.add_module("relu", nn.ReLU())
net.add_module("global_avg_pool", d2l.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, num_channels, 1, 1)
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(), nn.Linear(num_channels, 10)))

# 打印每个子模块的输出维度确保网络无误
X = torch.rand((1, 1, 96, 96))
for name, layer in net.named_children():
    X = layer(X)
    print(name, ' output shape:\t', X.shape)
# DenseBlosk_0  output shape:torch.Size([1, 192, 24, 24]) 192 = 64 + 32 * 4

# 获取数据并训练模型
batch_size = 128  # 原来为256，但会报错，所以设置小一点儿
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)

lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)

out5:

0  output shape:	 torch.Size([1, 64, 48, 48])
1  output shape:	 torch.Size([1, 64, 48, 48])
2  output shape:	 torch.Size([1, 64, 48, 48])
3  output shape:	 torch.Size([1, 64, 24, 24])
DenseBlosk_0  output shape:	 torch.Size([1, 192, 24, 24])
transition_block_0  output shape:	 torch.Size([1, 96, 12, 12])
DenseBlosk_1  output shape:	 torch.Size([1, 224, 12, 12])
transition_block_1  output shape:	 torch.Size([1, 112, 6, 6])
DenseBlosk_2  output shape:	 torch.Size([1, 240, 6, 6])
transition_block_2  output shape:	 torch.Size([1, 120, 3, 3])
DenseBlosk_3  output shape:	 torch.Size([1, 248, 3, 3])
BN  output shape:	 torch.Size([1, 248, 3, 3])
relu  output shape:	 torch.Size([1, 248, 3, 3])
global_avg_pool  output shape:	 torch.Size([1, 248, 1, 1])
fc  output shape:	 torch.Size([1, 10])
training on  cuda
epoch 1, loss 0.4221, train acc 0.848, test acc 0.885, time 69.5 sec
epoch 2, loss 0.2658, train acc 0.902, test acc 0.909, time 67.6 sec
epoch 3, loss 0.2284, train acc 0.917, test acc 0.883, time 67.6 sec
epoch 4, loss 0.2072, train acc 0.924, test acc 0.921, time 67.7 sec
epoch 5, loss 0.1887, train acc 0.930, test acc 0.905, time 67.9 sec

注意：若将batch_size设置为256，会报错

RuntimeError: CUDA error: CUBLAS_STATUS_NOT_INITIALIZED when calling `cublasCreate(handle)`

通过百度发现是batch_size设置过大，内存不够，改成128,运行成功！

参考链接：https://blog.csdn.net/li_jiaoyang/article/details/116047462?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-5.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-5.control

小结

1.在跨层连接上，不同于ResNet中将输入与输出相加，DenseNet在通道维上连结输入与输出。
2.DenseNet的主要构建模块是稠密块和过渡层。