凸优化理论基础3——凸集和凸锥重要例子
作者简介:秃头小苏,致力于用最通俗的语言描述问题
往期回顾:凸优化理论基础1–仿射集 凸优化理论基础2——凸集和锥
近期目标:拥有5000粉丝
支持小苏:点赞、收藏⭐、留言
文章目录
- 凸优化理论基础3——超平面和半空间
-
- 超平面
- 半空间
- 超平面和半空间是凸集
- 球和椭球
- 范数球和范数锥
- 多面体
- 单纯形
- 半正定锥
凸优化理论基础3——超平面和半空间
之前我们已经介绍了仿射集、凸集、凸锥等概念,这节将来介绍超平面和半空间。
超平面
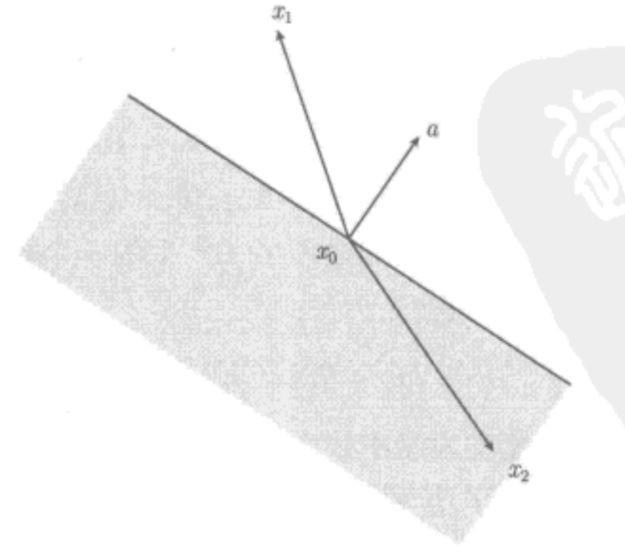
定义: 超平面是具有下面形式的集合
{ x ∣ a T x = b } , a ∈ R n , a ≠ 0 且 b ∈ R \{x|a^Tx=b\} \ , \quad a \in R^n,a\ne 0且b \in R {x∣aTx=b} ,a∈Rn,a=0且b∈R
上述定义还可以表示成以下形式:
{ x ∣ a T ( x − x 0 ) = 0 } \{x|a^T(x-x_0)=0\} {x∣aT(x−x0)=0}
其中 x 0 x_0 x0是超平面上的任意一点。不清楚观此视频这里来看看超平面的几何解释,如下:
半空间
定义: 半空间是具有下列形式的集合:
{ x ∣ a T x ≤ b } , a ≠ 0 \{x|a^Tx \le b\}, \quad a \ne 0 {x∣aTx≤b},a=0
一个超平面将 R n R^n Rn 划分为两个半空间。对于 R 2 R^2 R2来说,由 a T x ≥ b a^Tx \ge b aTx≥b决定的半空间(无阴影部分)是向 a a a扩展的半空间;由 a T x ≤ b a^Tx \le b aTx≤b决定的半空间(有阴影部分)是向 − a -a −a扩展的半空间。向量 a a a 是这个半空间向外的法向量。
超平面和半空间是凸集
首先直接给出以下结论:
- 超平面是仿射集
- 超平面是凸集
- 半空间不是仿射集
- 半空间是凸集
这里我想来证明证明超平面是凸集和半空间是凸集这两个结论【证明凸集及后面证明凸函数比较重要】
- 证明超平面是凸集
- 证明半空间是凸集
球和椭球
球的定义给出了三种方式,如下:
- B ( x c , r ) = { x ∣ ∣ ∣ x − x c ∣ ∣ 2 } ≤ r B(x_c,r)=\{x| \ ||x-x_c||_2\} \le r B(xc,r)={x∣ ∣∣x−xc∣∣2}≤r 。其中 r > 0 , ∣ ∣ ⋅ ∣ ∣ 2 r > 0,|| \cdot ||_2 r>0,∣∣⋅∣∣2 表示二范数,向量 x c x_c xc是球心,标量 r r r为半径。 B ( x c , r ) B(x_c,r) B(xc,r) 由距离不超过 r r r 的所有点组成
- B ( x c , r ) = { x ∣ ( x − x c ) T ( x − x c ) } ≤ r 2 B(x_c,r)=\{x | \ (x-x_c)^T(x-x_c)\} \le r^2 B(xc,r)={x∣ (x−xc)T(x−xc)}≤r2
- B ( x c , r ) = { x c + r u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } B(x_c,r)=\{x_c+ru \ | \ ||u||_2 \le 1\} B(xc,r)={xc+ru ∣ ∣∣u∣∣2≤1}
球也是凸集,证明如下:【证明用到了二范数的齐次性及三角不等式】
椭球也是凸集,其定义如下:
ε = { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } \varepsilon =\{x | \ (x-x_c)^TP^{-1}(x-x_c) \le 1 \} ε={x∣ (x−xc)TP−1(x−xc)≤1}
其中P是对称正定矩阵。
关于此部分视频链接:https://www.bilibili.com/video/BV1xp4y1C7z1/?spm_id_from=autoNext
范数球和范数锥
上面的球是针对二范数而言的,这里的范数球和范数锥类似于球的定义,不过不再限定二范数。
范数球定义: C = { x ∣ ∣ ∣ x − x c ∣ ∣ ≤ r } C=\{x| \ ||x-x_c|| \le r \} C={x∣ ∣∣x−xc∣∣≤r}
范数锥定义: C = { ( x , t ) ∣ ∣ ∣ x ∣ ∣ ≤ t } C=\{ (x,t) | \ ||x|| \le t \} C={(x,t)∣ ∣∣x∣∣≤t}
关于此部分视频链接:https://www.bilibili.com/video/BV1oA411t7L4/?spm_id_from=autoNext
多面体
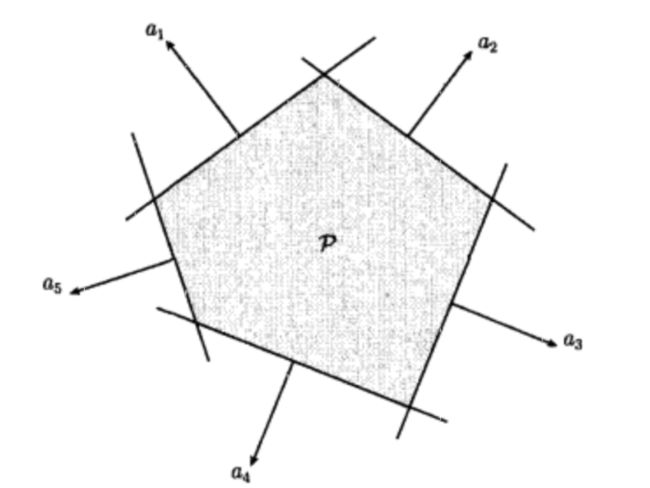
多面体被定义为有限个线性等式和不等式的解集,如下:
P = { x ∣ a j T x ≤ b j , j = 1 , ⋯ , m , c j T = d j , j = 1 , ⋯ , p } P=\{x | \ a^T_jx \le b_j \ ,j=1 \ , \cdots \ ,m \ , \ c^T_j=d_j \ , \ j=1 \ , \cdots, \ p\} P={x∣ ajTx≤bj ,j=1 ,⋯ ,m , cjT=dj , j=1 ,⋯, p}
由定义可以看出,多面体是有限个半空间和超平面的交集。仿射集(如子空间、超平面、直线)、射线、线段和半空间都是多面体,且多面体是凸集。下图中的多面体由五个半空间的交集构成:
单纯形
单纯形是一类重要的多面体。设 k + 1 k+1 k+1个点 v 0 , ⋯ , v k ∈ R n v_0, \cdots ,v_k \in R^n v0,⋯,vk∈Rn仿射独立,即 v 1 − v 0 , ⋯ , v k − v 0 v_1-v_0, \cdots ,v_k-v_0 v1−v0,⋯,vk−v0线性独立,那么这些点决定了一个单纯形,如下:
C = c o n v { v 0 , ⋯ , v k } = { θ 0 v 0 + ⋯ + θ k v k ∣ θ ⪰ 0 , 1 T θ = 1 } C=conv\{v_0, \cdots ,v_k \}=\{ \theta_0v_0+ \cdots +\theta_kv_k \ | \ \theta \succeq 0, \ 1^T \theta=1 \} C=conv{v0,⋯,vk}={θ0v0+⋯+θkvk ∣ θ⪰0, 1Tθ=1}
其中1表示所有分量均为一的向量。这个单纯形的仿射维数为k,因此也称为 R n R^n Rn 空间的k维单纯形。
下面给出一些常见的单纯形:
- 一维单纯形是一条线段
- 二维单纯形是一个三角形
- 三维单纯形是一个四面体
半正定锥
| 数学符号 | S n S^n Sn | S + n S^n_+ S+n | S + + n S^n_{++} S++n |
|---|---|---|---|
| 中文名称 | 对称矩阵 | 对称半正定矩阵 | 对称正定矩阵 |
| 数学表达式 | S n = { X ∈ R n × n ∣ X = X T } S^n=\{X \in R^{n\times n} | \ X=X^T\} Sn={X∈Rn×n∣ X=XT} | S + n = { X ∈ S n ∣ X ⪰ 0 } S^n_+=\{X \in S^n | \ X \succeq 0 \} S+n={X∈Sn∣ X⪰0} | S + n = { X ∈ S n ∣ X ≻ 0 } S^n_+=\{X \in S^n |\ X \succ 0 \} S+n={X∈Sn∣ X≻0} |
| 是否为凸集 | ✅ | ✅ | ✅ |
| 是否为凸锥 | ✅ | ✅ | ❎ |
此部分参考视频:https://www.bilibili.com/video/BV1Gt4y127oW/?spm_id_from=autoNext
如若文章对你有所帮助,那就
咻咻咻咻~~duang~~点个赞呗