深度学习入门——神经网络的正则化
神经网络中的正则化
学习记录自:deeplearning.ai-andrewNG-master
在开始之前,先让我们来看看正则化模型与非正则化训练效果。
非正则化模型与正则化模型的比较
预分类数据
非正则化分类结果
损失函数迭代图:
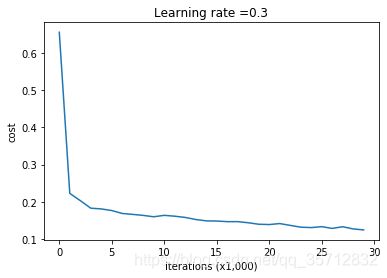
On the training set(训练集精度):
Accuracy: 0.94
On the test set(测试集精度):
Accuracy: 0.91
分类决策边界:

从分类结果来看测试精度为91%,损失函数优化时存在扰动。从分类决策边界来看,该分类模型过度拟合了训练集,拟合了许多噪声点。
## 正则化模型分类效果
L2正则

On the train set(训练集精度):
Accuracy: 0.93
On the test set(测试集精度):
Accuracy: 0.95
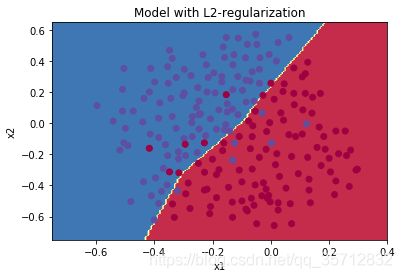
通过L2正则化,分类边界变得更趋于线性性与简单性,而测试精度也达到95%。避免了过拟合,具有更强的泛化能力。
神经网络中的正则化
一、正则化的概念及常用正则化方法
1.1 正则化
机器学习中的一个核心问题是设计不仅在训练数据上表现好,并且能在新输入上泛化好的算法。在机器学习中,许多策略显式地被设计来减少测试误差(可能会以增大训练误差为代价)。这些策略被统称伪正则化。
深度学习模型具有很高的灵活性和能力,如果训 练数据集不够大,将会造成一个严重的问题–过拟合。尽管它在训练集上效果很好,但是学到的网络不能应用到测试集中,所以在深度学习模型中使用正则化是必要的。
1.2 常用的正则化方法
神经网络模型中通常使用L2正则化对损失函数进行修正,另外Dropout正则化也常用。
L2正则化:
下面给出L2正则化之前损失函数表达式:

针对这个损失函数,给出它的正则化后的表达式:


L2正则化基于以下假设:权重较小的模型比权重较大的模型更简单。因此,通过对损失函数中权重的平方值进行惩罚,可以将所有权重驱动为较小的值,从而使模型更平滑,输出随着输入的变化而变化得更慢。
Dropout正则化:
Dropout提供了正则化一大类模型的方法,计算方便但功能强大。简单来说Dropout可以理解为在概率意义上随机删除神经网络中的节点,以此简化神经网络模型来防止过拟合的一种正则化方法,下图说明了Dropout的处理过程。

Dropout会在每次迭代中随机关闭一些神经元,其中涉及到正则化参数keep_prob,keep_prob是一个随机数,在正向传播时,我们给每一个神经元赋予一个概率,通过比较keep_prob与神经元的随机概率大小来给出决策。当该概率小于keep_prob时,我们关闭该神经元。做法是通过应用掩码来关闭正向传播过程中的某些神经元。
对于反向传播,将用相同的掩码重新来关闭相同的神经元,进而进行导数的计算。
1.3其他正则化方法
正则化的目的是为了防止过拟合带来的高方差,我们可以考虑采用数据扩增和提早结束训练来防止过拟合。
数据扩增
假设我们的数据集是图片,那对图片进行旋转、裁剪等可以达到数据扩增的目的,如下图所示。
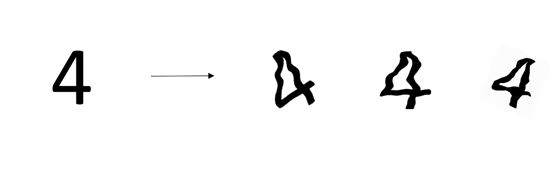
提早结束训练
过拟合一定程度上是由于训练过度导致的,为了防止过拟合带了的高方差,把方差和损失函数作为训练结束的评判标准可以一定程度上减少过拟合。下图是该方法的体现。

从上图来看,方差随着迭代次数的增加,会由小再变大,为了防止过拟合,在方差最小且损失函数比较小的时候提早结束训练。
二、正则化能减少过拟合的原因
2.1 过拟合
过拟合是指为了得到一致假设而使假设变得过度严格,如下图所示:
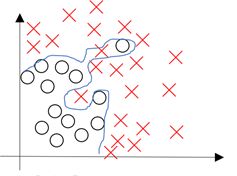
上图反映了对二维数据的分类,该分类器看似很好的拟合的边缘,达到的分类的目的,但是分类边界过于严格,这样的分类模型虽然在训练集中表现得很好,当把它应用到测试集中,预测结果却不会很好。
从上图来看,过拟合往往带着非线性性与复杂性,为了减少过拟合,我们采取某种方法来减少它的非线性性与复杂性。
2.2 正则化减少过拟合
以L2正则化为例,我们通过对权重项施以惩罚,在参数更新时,达到权重衰减的目的。权重衰减意味着衰减的神经元对神经网络的影响减小,使得原本复杂的神经网络变得简单,甚至简单到像Logistic回归一样,每层只具有一个神经元。
神经元作用的衰减让原本非线性的分类趋于线性分类,这样就一定程度避免了过拟合。
下图反映了神经网络正则化的过程,以及分类效果。
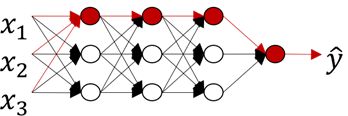

如图红色传播路线,正则化的神经网络变得简单化,最后得到的分类效果也更合理,具有更好的泛化效果。
正则化代码
本文以一个具有3层的神经网络为模型,输出层为sigmoid激活函数,其余层为Relu激活函数,给出该模型的正则化代码:
首先导入需要的包
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import scipy.io
非正则化模型(整合了正则化功能)
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
"""
实现3层神经网络: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
lambd -- 正则化参数
keep_prob - Dropout正则化参数
R返回值:
parameters -- 模型训练后的参数
"""
grads = {}
costs = [] # 损失值
m = X.shape[1] # 样本个数
layers_dims = [X.shape[0], 20, 3, 1] #神经网络层数 与 单元数
# 初始化参数
parameters = initialize_parameters(layers_dims)
# 迭代梯度下降
for i in range(0, num_iterations):
# 正向传播: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
#Dropout正则 舍去神经元
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# 损失函数
if lambd == 0:
cost = compute_cost(a3, Y)
else:
#含正则化的损失函数
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# 反向传播
assert(lambd==0 or keep_prob==1) # it is possible to use both L2 regularization and dropout,
# but this assignment will only explore one at a time
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
#L2正则反向
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
#Dropout正则反向
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# 参数更新
parameters = update_parameters(parameters, grads, learning_rate)
# 实时更新损失值
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
L2正则化
#L2正则化 损失函数
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
实现损失函数的L2正则化. See formula (2) above.
Arguments:
A3 -- 神经网络最后一层的激活值, 维度:(output size, number of examples)
Y -- 样本标签, 维度: (output size, number of examples)
parameters -- 参数字典
返回值:
cost - 正则化后的损失函数
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y) # 损失函数 项
#正则项 (lambad/2m)*范数的平方 对于这个3层的神经网络 就是每一层的w平方之和 再相加
L2_regularization_cost = (1./m*lambd/2)*(np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
#正则化后的损失函数值
cost = cross_entropy_cost + L2_regularization_cost
return cost
#L2正则化 反向传播 梯度
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
实现L2正则化后的反向传播
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache --正向传播时的 缓存值
lambd -- 正则化参数
返回值:
gradients -- 各参数的梯度字典
"""
m = X.shape[1]
#读取每一层的信息
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
#添加正则项后 对w后求导为 (lamda/m)*w
dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m * W3
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * W2
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * W1
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
Dropout正则化
"""
Dropout正则化是广泛用于深度学习的正则化技术,它会在每次迭代中随机关闭一些神经元
练习为第一和第二隐藏层添加Dropout
"""
#Dropout 正则化 正向传播
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
实现Dropout正则化: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
Arguments:
X -- input dataset, of shape (2, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
keep_prob - 关闭隐藏单元的概率
Returns:
A3 -- 神经网络最后一层的激活值 (输出值)
cache -- tuple, information stored for computing the backward propagation
"""
# 首先读取参数
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# 第一层的dropout
D1 = np.random.rand(A1.shape[0],A1.shape[1]) # Step 1: 得到第一层的随机矩阵
D1 = D1 < keep_prob # Step 2: 把随机矩阵中 小于keep_prob的值全部更新为0
A1 = A1 * D1 # Step 3: 相乘 达到 权重置0的效果(神经元清除)
A1 = A1 / keep_prob # Step 4: 保证期望不变
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
#第二层的dropout
D2 = np.random.rand(A2.shape[0],A2.shape[1])
D2 = D2 < keep_prob
A2 = A2 * D2
A2 = A2 / keep_prob
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
#注意 D1 D2 也要保存下来
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
#Dropout正则化 反向传播
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
实现Dropout正则化 的反向传播
Arguments:
X -- input dataset, of shape (2, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- 正向传播时的缓存值
keep_prob - dropout正则化参数
返回值:
gradients -- 各参数的梯度字典
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
#同样利用 D2将 计算到的梯度 置0 (某些神经元的清除)
dA2 = dA2 * D2
dA2 = dA2 / keep_prob #保证期望
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
#利用D1来 进行 梯度置0 (某些神经元的清除)
dA1 = dA1 * D1
dA1 = dA1 / keep_prob #保证期望
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
下面是各正则化方法的调用格式:
以Dropout正则化为例,正则化参数keep_prob为0.86,学习率为0.3。
#模型训练
parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
好了,现在就可以用训练得到的参数去进行预测与分类了!