粒子群算法求解电力系统环境经济调度（Python代码实现）

目录

1 电力系统环境经济调度数学模型

2 改进粒子群算法解决 （Python代码实现）

2.1 知识回顾

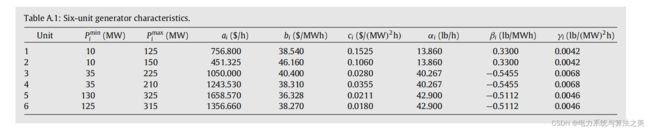
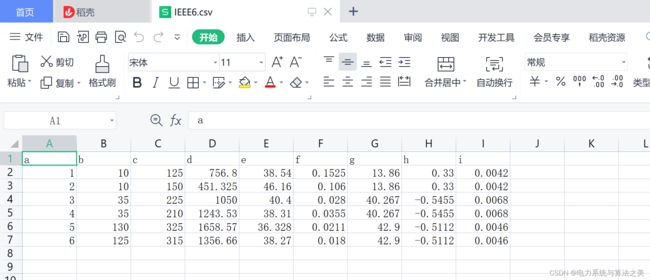
2.2 案例数据

2.3 Python代码

2.4 结果 

3 展望

---

1 电力系统环境经济调度数学模型

 

---

2 改进粒子群算法解决 （Python代码实现）

2.1 知识回顾

很多粉丝私聊我，让我电气论文的写点简单能入门的，所有今天这个比较简单，我们先回顾一下相关知识点：

*智能优化算法（持续更新中......）

智能优化算法——粒子群算法（Matlab实现）

粒子群算法——Python实现

2.2 案例数据

我弄成了一个文档，对应起来：

2.3 Python代码

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

# ~~~~~~~~~~~~~导入相关库~~~~~~~~~~·
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl

mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
import matplotlib

matplotlib.use('TkAgg')
from tqdm import tqdm  # 进度条设置

# ~~~~~~~~~~~~~~~~~~~~~读取文件~~~~~~~~~~~~~~~~~~~~~~
file=pd.read_csv('IEEE6.csv')#机组参数
P_max = file['b']  #机组上限
P_min = file['c']  # #机组下限


# ~~~~~~~~~~~~~~~~~机组特性系数~~~~~~~~~~~~~~~~~~~~~~~~·
ai = file['d']
bi=file['e']
ci=file['f']

# ~~~~~~~排放特性系数~~~~~~~~~~~~~~~~·
ali=file['g']
beti=file['h']
gari=file['i']

# ~~~~~~~~~~~~~~~~~~~~~~~粒子群算法~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~·
class Liqun:
    def __init__(self, Pload1,  P_max,P_min,ai,bi,ci,ali,beti,gari):
        self.Pload1 = Pload1  # 负荷
        self.P_max = P_max  #机组上限
        self.P_min = P_min  #机组下限
        self.ai=ai
        self.bi=bi
        self.ci=ci
        self.ali=ali
        self.beti=beti
        self.gari=gari

        # ~~~~~~~~PSO的参数~~~~~~~~~~~~~~~·
        self.w = 1  # 惯性因子，一般取1
        self.c1 = 2  # 学习因子1，一般取2
        self.c2 = 2  # 学习因子2，一般取2
        self.m = 500  # 种群大小，即种群中小鸟的个数
        self.iter_num = 100  # 算法最大迭代次数
        self.max_vel = 0.5  # 限制粒子的最大速度为0.5
        self.min_vel = -0.5  # 限制粒子的最小速度为-0.5
        self.a1= 0.7  # 总燃料约束权重
        self.a2= 0.3  # 污染排放量权重

    # ~~~~~~~~~~~~~初始化群群体~~~~~~~~~~~~~~~·
    def InitializeX(self):
        """
    :return: 群体[G1，G2，G3，G4，G5，G6]
    """
        X = np.zeros((self.m, 6))  # 初始化群体，6代表 个机组出力
        for n in range(self.m):  # 遍历每一个粒子
            X[n, 0] = np.random.uniform(10, 125, 1)[0]  # G1
            X[n, 1] = np.random.uniform(10, 150, 1)[0]  # G2
            X[n, 2] = np.random.uniform(35, 225, 1)[0]  # G3
            X[n, 3] = np.random.uniform(35, 210, 1)[0]  # G4
            X[n, 4] = np.random.uniform(130,325, 1)[0]  # G5
            X[n, 5] = np.random.uniform(125,315, 1)[0]  # G6
        return X

    # ~~~~~~~~~~~~~~~~~~~定义目标函数、和对应的惩罚项~~~~~~~~~~~~~~~~~~~·
    # ~~~~~1 目标函数：系统运行成本~~~~~

    def function1(self, X1):
        """
        个体目标函数
        :param X1:  （个体[G1，G2，G3，G4，G5，G6]
        :return: 函数1目标函数值
        """
        SUMCOST = []  # 存储总的成本
        for i in range (5):  # 遍历每一台机组
            cost = self.ci[i] * X1[i] * X1[i] + self.bi[i]* X1[i] +self.ai[i] #
            SUMCOST.append(cost)
        return np.sum(SUMCOST)

    #~~~~~~~~~~~~~~总污染排放量~~~~~~~~~~~~··
    def function2(self, X1):
        """
        个体目标函数
        :param X1:  （个体[G1，G2，G3，G4，G5，G6]
        :return: 函数2目标函数值
        """
        emission=[] #储存总的污染排放量
        for i in range(5):
            e=ali[i]+beti[i]*X1[i]+gari[i]*X1[i]*X1[i]
            emission.append(e)
        return np.sum(emission)


    # ~~~~平衡约束~~~~~~·
    def calc_e1(self, X1):
        """
    函数1 对应的个体惩罚项
    :param X1: （个体[G1，G2，G3，G4，G5，G6]
    :return:
    """
        cost=np.abs(X1[0]+X1[1]+X1[2]+X1[3]+X1[4]+X1[5]-self.Pload1)
        return cost

    # ~~~~~~~~~~~~~~~~粒子群速度更新公式~~~~~~~~~~~~~~~~~~~·
    def velocity_update(self, V, X, pbestX, gbestX):
        """
    :param V: 群体速度
    :param X: 群体位置[G1，G2，G3，G4，G5，G6]
    :param pbestX: 种群历史最优位置
    :param gbestX: 全局最优位置
    :return:
    """
        r1 = np.random.random((self.m, 6))
        r2 = np.random.random((self.m, 6))
        V = self.w * V + self.c1 * r1 * (pbestX - X) + self.c2 * r2 * (gbestX - X)  # 直接对照公式写就好了
        # 防止越界处理
        V[V > self.max_vel] = self.max_vel
        V[V < self.min_vel] = self.min_vel
        return V

    # ~~~~~~~粒子群位置更新公式~~~~~~~~~~~~~~~·
    def position_update(self, X, V):
        """
    根据公式更新粒子的位置
    :param X: 粒子当前的位置矩阵，维度是 (self.m, 6)
    :param V: 粒子当前的速度举着，维度是 (self.m, 6)
    """
        X = X + V  # 更新位置

        for n in range(self.m):  # 遍历每一个粒子
            if X[n, 0] < 10 or X[n, 0] > 125:  # G1
                X[n, 0] = np.random.uniform(10, 125, 1)[0]  # G1
            if X[n, 1] < 10 or X[n, 1] > 150:  # G2
                X[n, 1] = np.random.uniform(10, 150, 1)[0]  # G2
            if X[n, 2] < 35 or X[n, 2] > 225:  # G3
                X[n, 2] = np.random.uniform(35, 225, 1)[0]  # G4
            if X[n, 3] < 35 or X[n, 3] > 210:  # G5
                X[n, 3] = np.random.uniform(35, 210, 1)[0]  # G8
            if X[n, 4] < 130 or X[n, 4] > 325:  # G11
                X[n, 4] = np.random.uniform(130, 325, 1)[0]  # G1
            X[n, 5] = self.Pload1 - X[n, 0] - X[n, 1] - X[n, 2] - X[n, 3] - X[
                n, 4]  # 负荷平衡得到 G13 出力
            while (X[n, 5] < 125) or (X[n, 5] > 315):  # 如果G13 上下限违规
                X[n, 0] = np.random.uniform(10, 125, 1)[0]  # G1
                X[n, 1] = np.random.uniform(10, 150, 1)[0]  # G2
                X[n, 2] = np.random.uniform(35, 225, 1)[0]  # G3
                X[n, 3] = np.random.uniform(35, 210, 1)[0]  # G4
                X[n, 4] = np.random.uniform(130, 325, 1)[0]  # G5
                X[n, 5] = self.Pload1- X[n, 0] - X[n, 1] - X[n, 2] - X[n, 3] - X[
                    n, 4]  # 负荷平衡得到 G13 出力

        return X

    

2.4 结果 

100%|██████████| 100/100 [00:03<00:00, 26.09it/s]
迭代最优变量是： [ 41.42608737  36.4634904  182.18059225 134.44146782 290.55563308
 314.93272908]
迭代最优目标函数1(总燃料成本）：35260.71417
迭代最优目标函数2(总污染排放量）：605.34109
迭代最优的惩罚项： 0.0

完整代码——请博主喝杯奶茶吧 ：粒子群算法求解环境经济调度（Python代码实现）

3 展望

后期将在此基础上加大难度，10机组有阀点效应的，有网损的。最后再来40机组的，难度慢慢加大。下集预告：