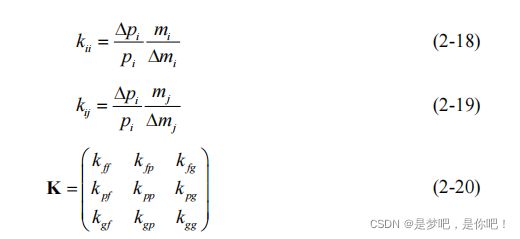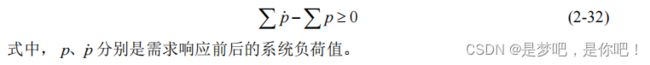需求响应对配电网供电可靠性影响分析（Python代码实现）

目录

1 引言

2 考虑客户意愿的分时电价需求侧响应模型 

2.1 电价伸缩系数分析

2.2 需求侧响应数学模型 

2.2.1 主观限制 

2.2.2 客观限制 

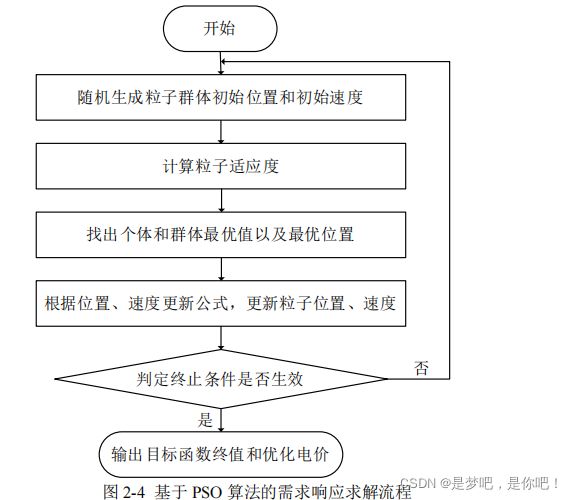
2.3 基于 PSO 算法的需求响应模型

3 案例 

3.1 数据

3.2 基础数据绘图  

---

1 引言

       提高配电网的供电能力以满足用户用电需求已成为我国电网规划亟待解决的问题之一。在含分布式电源的配电网中采用需求侧响应策略，可以在一定程度上降低系统的峰谷差和负荷波动，缓解供电压力。配电网中引入需求侧响应策略后，需求侧响应对配电网供电能力提升的延续性依赖于客户的主观意愿，传统的从技术层面考察系统供电能力的评估体系将不再完全适用。因此，合理制定需求侧响应策略，完善现有供电能力评估体系，科学全面的评估需求侧响应对配电网供电能力的影响，对配电网的规划、运行具有十分重要的指导作用。

       电力客户参与需求侧响应的意愿直接影响需求侧响应策略的实施程度。为了在需求侧响应模型中体现客户的主观意愿，在考虑传统的电价和负荷限制基础上，提出客户舒适性和支出合理性限制条件，通过模糊传递闭包法对峰谷时段进行合理的划分，建立考虑客户舒适性和支出合理性需求侧响应模型，并使用粒子群算法进行电价寻优。

2 考虑客户意愿的分时电价需求侧响应模型 

2.1 电价伸缩系数分析

       在经济学领域，通常采用价格伸缩系数来描述商品的需求对于价格敏感程度。电力能源作为商品，同样可以采用伸缩系数来描述电力需求和电价之间的关系。--方面，电价的变化可以影响电力客户的用电行为，进而影响用电量;另一方面，客户用电量的改变，也可以指导供电侧电价的制定，使电力企业获得更高的收益。客户用电量与电价之间的关系采用电价伸缩系数k来表示。k可以定义为客户用电量波动率与价格波动率的比值:

                                  

式中，p 和 m 分别表示该时刻初始的用电量和价格，∆p和∆m 分别表示该时刻的用电量和电价的改变量。

       实际生产生活中，电力客户的用电行受多重因素影响。一方面，当前时段电力价格的变化可能会导致当前时段用电行为的改变，产生了用电量的增减；同时，其他时段的电价变化也会对当前时段客户的用电行为产生影响，即产生了用电量的转移。所以，在分析价格伸缩性时，需要综合考虑上述两种伸缩变化。可定义第 i 时段的自伸缩系数为kii，第 i 时段对第 j 时段的互伸缩系数为kij，如式(2-18)~式(2-19)。在得到自伸缩系数kii和互伸缩系数kij后，则能形成需求侧响应电价伸缩系数矩阵 K，如式

(2-20)：

         

式中，下角标 f、p、g 代表伸缩系数归属的不同时间段。

显然地，K 矩阵对角线元素k ff 、 k pp 、kgg 表征了当前时间电价变化与需求侧用电量之间的相互作用，是自伸缩系数；而矩阵中其他元素则表征了不同时间内电价变化与需求侧用电量的相互作用，是互伸缩系数。进一步地，在采用了分时电价之后，各个时间段用电变化量ΔP ，如式(2-21)：

         

式中， p 、m 分别为采用需求侧响应策略之前的用电量和电价。综上。采用需求侧响应之后各个时间的负荷需求量矩阵为

                                 

2.2 需求侧响应数学模型 

       对于配电网而言，如果在其允许的范围内峰值负荷过大，会导致其转带备用容量不足，负荷波动率较高，容易影响该配电网的稳定性。同时，通过柯西-施瓦茨不等式证明了网损与最高-最低负荷比率成正比，即日内负荷的峰谷差越小，系统线损率越低。可见，缩小电网的高低负荷比率能够有效降低网损，提高系统负荷率，从而提升设备利用率。

       基于上述分析，设置日最高负荷与日最高-最低负荷比率为规划目标。因为这两个目标可以从直观上判断出系统的供电能力，故也可以定义这两个规模目标为系统的显性供电能力，其值越小，系统的显性供电能力越好。规划目标如式(2-23)~式(2-24)：

          

式中，  和 分别为采用需求侧响应策略之后的峰负荷最大值和峰谷负荷差最大值。显然，求解此问题涉及多个规划目标。对于这类问题求解，通常有两种做法，即将多个规划目标转化为单一目标进行求解或者采用分层序列法。这里对每个目标进行数据标准化后运用线性加权和法将多个规划目标转化为单一目标；而后设置权系数µ1 、 µ2 ，有 µ1+µ2=1，作规划目标的线性加权和，得到最终规划目标，如式(2-25)：

  

式中， 和

分别为采用需求侧响应之前系统的峰负荷最大值和峰谷负荷差最大值。确定了规划目标之后需要根据电力系统运行特点以及电力市场相关经验设置合理的边界条件.

2.2.1 主观限制 

某些时段过高的价格会导致客户支出过高，所以需要考虑客户负担的合理性，即在应用需求侧响应策略后客户所需负担的总费用不应升高。据此，定义客户支出合理性指标 H1，如式(2-26)：

          

式中，和分别表示需求侧响应前后第 t 时段客户负担电费值。

       同时，在市场经济中，欲达到供需双方利益的最大化，不仅需要考虑商品的成本和用户的支出，同时也需要考虑商品是否满足需求方的舒适性。分析需求侧响应策略的削峰填谷作用可知，微观上，在采用需求侧响应策略之后，一部分客户会根据分时电价调整自身的用电安排，这会导致自身的舒适性降低，而使个人日用电需求曲线变的平缓；宏观上，电力日负荷曲线是全体电力客户当日用电情况的集中反映，当部分用户因参与需求侧响应而使得用电曲线变的平缓时，电网的日负荷曲线会随之变的平缓，日负荷标准差也会相应减小。

      通过上述分析可知，负荷曲线的标准差可以从一定程度上体现客户对于需求侧响应的参与度。随着参与度的提升，负荷曲线的标准差也会在一定程度上减小，但是客户被迫调整或者削减原有的用电安排的情况就会越多，导致舒适性降低。基于上述分析，定义客户舒适性指标 H2如式(2-27)：

2.2.2 客观限制 

根据经济学相关知识可知，通常情况下商品的价格量是一个合理范围内的正数； 同时，对于客户而言，为保证正常的生产生活用电需求，电力负荷高峰时的电费不可 以过高；而对于供电企业而言，为保证盈利，则在电力负荷低谷时电费不能过低；此 外，根据电力市场相关经验易知，商品定价时需要保证一定的价格梯度，即低谷时刻 价格须比平时价格低，且平时价格也须比高峰时段价格低。客观价格边界条件如式(2- 31)：

此外，在采用需求侧响应策略之后，为使效益最大化时不造成容量浪费，需要尽可能的保持配电网内部负荷值不小于原始配电网内部的负荷值，如式(2-32)：

2.3 基于 PSO 算法的需求响应模型

       

3 案例 

3.1 数据

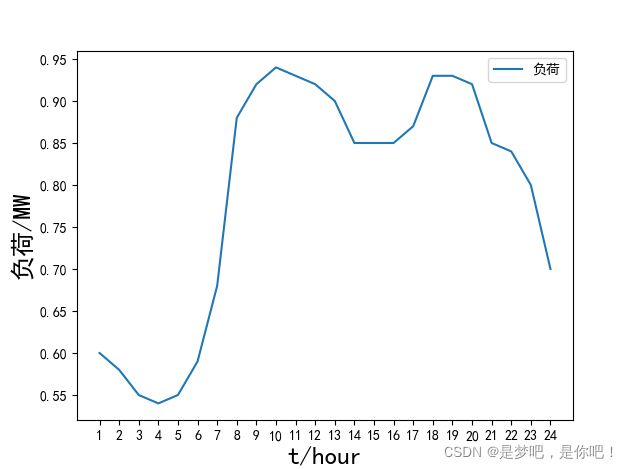
基础负荷数据（MW）

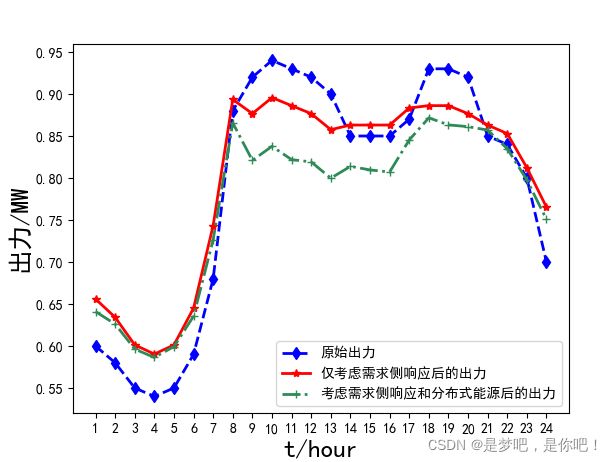
Pload=np.array([0.6,0.58, 0.55, 0.54, 0.55, 0.59, 0.68, 0.88, 0.92, 0.94, 0.93, 0.92, 0.9, 0.85, 0.85, 0.85, 0.87, 0.93, 0.93, 0.92, 0.85, 0.84, 0.8, 0.7])

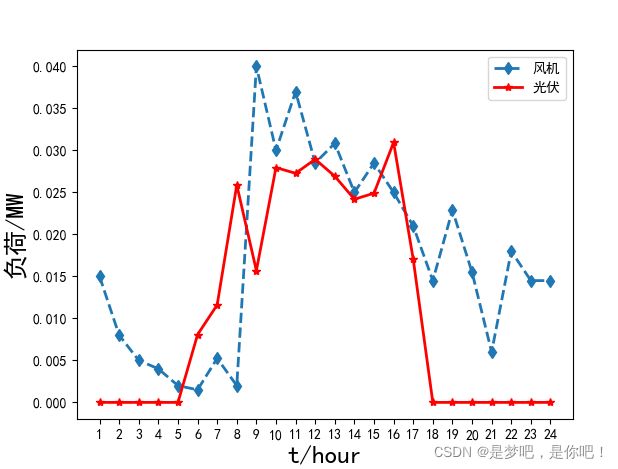
风机出力(MW)

PF=0.5*np.array([0.03, 0.016, 0.010, 0.008, 0.004, 0.003, 0.01049, 0.004, 0.08, 0.06,   0.074,  0.057,0.0617, 0.05, 0.057, 0.050, 0.042, 0.029,0.0458, 0.031, 0.012, 0.036, 0.029, 0.029])

光伏出力(MW)

PS=0.5*np.array([0, 0,0,0,0,0.01613917,0.02322205, 0.05175432, 0.0313843,  0.05591635, 0.0545465,  0.05789205,0.05384659, 0.04837572, 0.04980761, 0.06190041, 0.03408133, 0,0,  0,0,0, 0, 0])

3.2 基础数据绘图  

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
import matplotlib;
matplotlib.use('TkAgg')  #解决在PyCharm中不显示绘图；
'''matplotlib的use()命令其实是用来配置matplotlib的backend （后端）的命令
也就是说，Pycharm运行的时候，默认的后端是Qt5Agg。
实际上，Agg 渲染器是非交互式的后端，没有GUI界面，所以不显示图片，它是用来生成图像文件。
Qt5Agg 是意思是Agg渲染器输出到Qt5绘图面板，它是交互式的后端，拥有在屏幕上展示的能力3。'''

Pload=np.array([0.6,0.58, 0.55, 0.54, 0.55, 0.59, 0.68,
 0.88, 0.92, 0.94, 0.93, 0.92, 0.9, 0.85,
 0.85, 0.85, 0.87, 0.93, 0.93, 0.92, 0.85, 0.84, 0.8, 0.7])

plt.plot(Pload,label="负荷")
plt.xticks(np.arange(0,24,1),np.arange(1,25,1))
plt.xlabel('t/hour',fontsize=18)    #字体大小18
plt.ylabel('负荷/MW',fontsize=18)
plt.legend()
plt.show()


PF=0.5*np.array([0.03, 0.016, 0.010, 0.008, 0.004, 0.003,
 0.01049, 0.004, 0.08, 0.06,   0.074,  0.057,
 0.0617, 0.05, 0.057, 0.050, 0.042, 0.029,
 0.0458, 0.031, 0.012, 0.036, 0.029, 0.029])

PS=0.5*np.array([0, 0,0,0,0,0.01613917,
 0.02322205, 0.05175432, 0.0313843,  0.05591635, 0.0545465,  0.05789205,
 0.05384659, 0.04837572, 0.04980761, 0.06190041, 0.03408133, 0,
 0,  0,0,0, 0, 0])
plt.plot(PF,marker='d',linestyle='--',linewidth=2,label="风机")
plt.plot(PS,color='r',marker='*',linestyle='-',linewidth=2,label="光伏")
plt.xticks(np.arange(0,24,1),np.arange(1,25,1))
plt.xlabel('t/hour',fontsize=18)
plt.ylabel('负荷/MW',fontsize=18)
plt.legend()
plt.show()

      

         

写在最后：本文是对这篇文献的复现

                    

下面只展示部分结果： 

                            

                                   （我以前的网名就是是梦吧，是你吧）

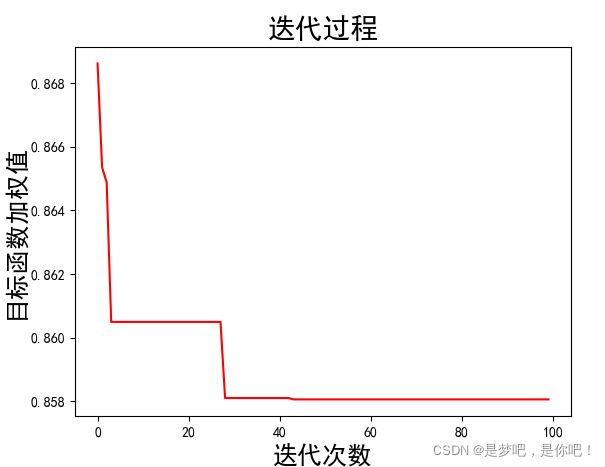
100%|██████████| 100/100 [01:39<00:00,  1.00it/s]
原始电价 [[0.6]
 [0.6]
 [0.6]]
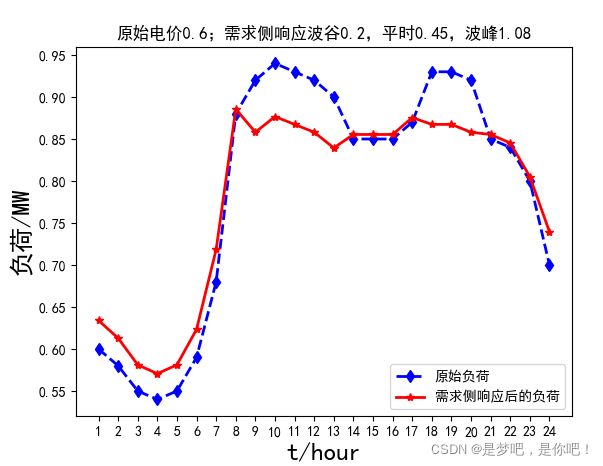
原始负荷的出力峰值 0.94
原始负荷的出力峰谷差 0.3999999999999999
客户支出合理性指标H1的要求是 1.001
需求响应后客户舒适性指标H2的要求是 0.76
-----------需求侧响应后的----------
最优目标函数加权值是：0.85571
最优解（电价)
 [0.23954568 0.54435494 0.90615727]
需求响应后客户支出合理性指标H1: 1.0040081988237473
需求响应后客户舒适性指标H2: 0.7610906412369757
需求响应后的出力峰值 0.8921229159238201
需求响应后的出力峰谷差 0.30493973487376314