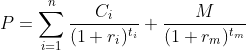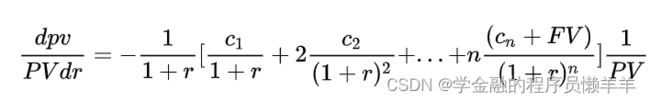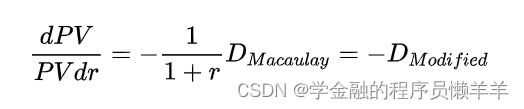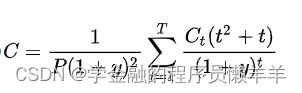【金融系列】使用Python分析债券,画零息利率曲线,对债券进行精确定价,计算债券的麦考利久期、修正久期和凸度,并进行价格敏感性分析
目前许多代码和资源在进行债券定价时,大多以债券发行日作为贴现值的时间点,但在实际应用中我们常常需要对早就发行的债券进行定价,这就需要计算准确的现金流、现金流日距离当前贴现时间点的时间距离和不同时间距离的零息利率,这一过程会较多使用插值法,还涉及到时间的转换。此外,本文还进行了麦考利久期、修正久期和凸度的计算,并使用久期凸度分析了价格的敏感性。
目录
1 主要步骤概述
2 使用插值法计算特殊点零息利率,并画出收益率曲线
3 对债券进行精确定价
4 计算债券的麦考利久期、修正久期和凸度,并进行价格敏感性分析
1 主要步骤概述
国家开发银行发行了200亿元的“22国开05”债券(代码220205.IB),在“中国货币网”查找该债券的关键信息:面值、期限、票面利率、付息频次、起息日等。并请用python程序完成了下列任务:
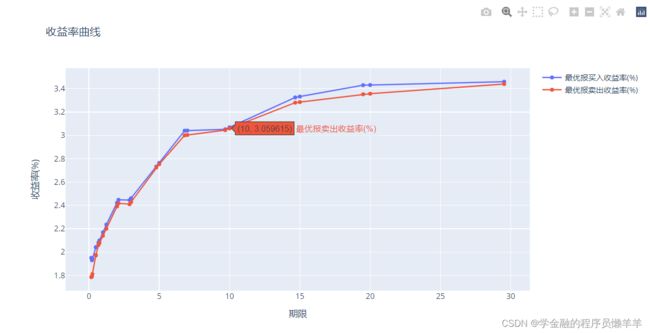
1、登录“中国货币网”,查找“基准利率”中的“实时收益率曲线”,下载“政策性金融债”的实时收益率数据到excel,python读入这些数据,并利用数据作图将其可视化。
2、计算“22国开05”各个未来现金流的剩余期限,利用插值法得到这些时刻对应的即期利率(即零息债券的收益率)。然后,再利用前面得到的零息利率对“22国开05”债券进行精确定价(净价)。
3、利用前面得到的数据计算该债券的修正久期和凸性值;假定即期利率曲线(零息利率曲线)发生了平移,即每期都增加100个基点,请用久期和凸性方法重新估计债券价格。
2 使用插值法计算特殊点零息利率,并画出收益率曲线
以下数据为2022年5月10日国开行的不同剩余期限的基准债券的数据。我们以一下数据作为初始数据,并使用插值法,计算0~30年中特殊关键时点的零息利率,并画出图。
| 标准期限(年) | 基准债券 | 剩余期限(年) | 最优报买入收益率(%) | 最优报卖出收益率(%) | |
|---|---|---|---|---|---|
| 0 | 0.083 | 15国开16 | 0.1671 | 1.9500 | 1.7848 |
| 1 | 0.250 | 21国开11 | 0.2192 | 1.9298 | 1.7902 |
| 2 | 0.500 | 21国开16 | 0.4904 | 2.0401 | 1.9700 |
| 3 | 0.750 | 22国开01 | 0.6795 | 2.0800 | 2.0600 |
| 4 | 1.000 | 20国开07 | 1.2438 | 2.2350 | 2.2000 |
| 5 | 2.000 | 21国开07 | 2.1041 | 2.4475 | 2.4175 |
| 6 | 3.000 | 22国开绿债02清发 | 2.8932 | 2.4450 | 2.4100 |
| 7 | 5.000 | 22国开03 | 4.7945 | 2.7325 | 2.7250 |
| 8 | 7.000 | 22国开04 | 6.8082 | 3.0400 | 2.9999 |
| 9 | 10.000 | 22国开05 | 9.6904 | 3.0520 | 3.0450 |
| 10 | 15.000 | 17国开02 | 14.6685 | 3.3250 | 3.2800 |
| 11 | 20.000 | 21国开20 | 19.4986 | 3.4300 | 3.3520 |
| 12 | 30.000 | 21国开21 | 29.5288 | 3.4600 | 3.4400 |
数据导入:
#导入包
import pandas as pd
import numpy as np
import plotly.graph_objects as go
import plotly.offline as of # 这个为离线模式的导入方法
#数据导入
data_policyfinancialdebt = pd.read_excel('国开行实时收益率_5.10.xlsx')
使用插值法将收益率补齐:
#使用插值法将收益率补齐
duration = sorted(np.concatenate((data_policyfinancialdebt['标准期限(年)'].values,data_policyfinancialdebt['剩余期限(年)'].values)))
duration.pop(0)
duration.pop()
f1=interpolate.interp1d(x=data_policyfinancialdebt['剩余期限(年)'],y=data_policyfinancialdebt['最优报买入收益率(%)'],kind='slinear')
f2=interpolate.interp1d(x=data_policyfinancialdebt['剩余期限(年)'],y=data_policyfinancialdebt['最优报卖出收益率(%)'],kind='slinear')
rates_new_buy = f1(duration)
rates_new_sell = f2(duration)画收益率曲线图:(这里用到了我最近发现的一个更好地数据可视化工具plotly,十分好用,后面另写文章介绍)
# 画收益率曲线图
line1 = go.Scatter(y=rates_new_buy, x=duration,mode='lines+markers', name='最优报买入收益率(%)') # name定义每条线的名称
line2 = go.Scatter(y=rates_new_sell, x=duration,mode='lines+markers', name='最优报卖出收益率(%)')
fig = go.Figure([line1, line2])
fig.update_layout(
title = '收益率曲线', #定义生成的plot 的标题
xaxis_title = '期限', #定义x坐标名称
yaxis_title = '收益率(%)'#定义y坐标名称
)
fig.show()输出:
3 对债券进行精确定价
债券价值=未来各期利息收入的现值合计+未来到期本金或售价的现值,债券价值是指进行债券投资时投资者预期可获得的现金流入的现值。
债券的现金流入主要包括利息和到期收回的本金或出售时获得的现金两部分。
因此对债券进行精确定价,需要知道该债券的每一现金流,以及可以获得的每一现金流距离贴现点的时间长度,以及这些时间长度所对应的零息利率。如上图中的公式,C(票息)和M(债券面值)为每一现金流,实际上每一期的C可能不同,ri对应不同时间长度的零息利率,也就是每一现金流有不同的r。
计算债券的现金流列表,每一现金流对应的零息利率,每一现金流距离指定时间点间的时间距离的函数:
#计算债券的现金流列表,每一现金流对应的零息利率,每一现金流距离指定时间点间的时间距离
def cal_cashrtime(bar,couponrate,startdate,next_coupon_date,enddate, duration , rate_list,freq = 1):
"""
计算债券的现金流列表,每一现金流对应的零息利率,每一现金流距离指定时间点间的时间距离
Args:
startdate: 需折现到的日期
coupon_date: 下一次付息日
enddate: 债券到期鈤日
freq: 年付息次数
duration: 用于插值法的期限list
rate_list: 用于插值法的利率list
Returns:
现金流list,现金流时间距离list,现金流对应零息利率list
"""
cashflow = []
time_list = []
date_temp = next_coupon_date
while(enddate>=date_temp):
cashflow.append(bar * couponrate)
time_list.append((date_temp-startdate)/timedelta(365))
date_temp = (date_temp + relativedelta(years=1))
cashflow.append(bar)
time_list.append((enddate-startdate)/timedelta(365))
#插值法获取零息利率
f=interpolate.interp1d(x=duration,y=rate_list,kind='slinear')
r_list = list(f(time_list))
return cashflow,time_list,r_list债券精确定价函数:
#债券精确定价函数
def bond_preciseprice(bar,coup_rate,r_list,time_list):
"""
计算一只债券的精确定价
Args:
bar: 债券的票面价值
coup_rate: 债券的票面利率
r_list: 每一现金流对应的零息利率
time_list: 每一现金流离目前的时间点
Returns:
返回债券的精确定价
"""
per_coupon = bar * coup_rate
discount_coupon = 0
for r,time in zip(r_list,time_list):
if(r != r_list[-1]):
discount_coupon = discount_coupon + per_coupon/(1 + r*0.01)**time
return (discount_coupon + bar/(1 + r_list[-1]*0.01)**time_list[-1])配置22国开05债券的信息并调用函数:
#配置22国开05信息配置
bar,couponrate,startdate,next_coupon_date,enddate = 100,0.03,datetime(2022,5,10),datetime(2023,1,16),datetime(2032,1,17)
cashflow,time_list,r_list = cal_cashrtime(bar,couponrate,startdate,next_coupon_date,enddate, duration ,rates_new_sell)
price2205 = bond_preciseprice(bar,couponrate,r_list,time_list)
print("22国开05的定价为:",price2205)输出:
22国开05的定价为: 100.76765580931195
4 计算债券的麦考利久期、修正久期和凸度,并进行价格敏感性分析
麦考利久期(Macaulay duration) 。久期的概念最早是麦考利 (Frederick Robertson Macaulay (1882.8.12–1970.3) )在1938年提出来的,所以又称麦考利久期(简记为D)。麦考利久期是使用加权平均数的形式计算债券的平均到期时间。它是债券在未来产生现金流的时间的加权平均,其权重是各期现值在债券价格中所占的比重。
修正久期是对于给定的到期收益率的微小变动,债券价格的相对变动与其麦考利久期的比例。这种比例关系是一种近似的比例关系,以债券的到期收益率很小为前提。是在考虑了收益率的基础上对麦考利久期进行的修正,是债券价格对于利率变动灵敏性的更加精确的度量。
凸性( Convexity )是收益率变化 1 %所引起的久期的变化。用来衡量债券价格收益率曲线的曲度。凸性越大,债券价格曲线弯曲程度越大,用修正久期度量的利率风险所产生的误差越大。
麦考利久期代码实现:
#计算麦考利久期
def mcduration(cashflow,time_list,r_list,presentvalue):
mcduration = 0
for cash,time,r in zip(cashflow,time_list,r_list):
mcduration = mcduration + time * ( cash / (1 + r * 0.01) ** time) / presentvalue
return mcduration计算修正久期(涉及到到期收益率ytm的计算):
#计算修正久期
def dduration(cashflow,time_list,r_list,presentvalue):
return mcduration(cashflow,time_list,r_list,presentvalue)/(1+YTM(presentvalue,cashflow,time_list,bar))
#计算ytm
def YTM(presentvalue,cashflow,time_list,bar):
def ff(y):
cash_all = []
for cash,time in zip(cashflow,time_list):
if(cash != cashflow[-1]):
cash_all.append(cash/pow(1+y,time))
return np.sum(cash_all)+cashflow[-1]/pow(1+y,time_list[-1])-presentvalue
return float(so.fsolve(ff,0.01))计算凸性:
#计算凸性
def Convexity(cashflow,time_list,presentvalue):
temp = []
ytm = YTM(presentvalue,cashflow,time_list,bar)
for cash,time in zip(cashflow,time_list):
temp.append(cash*(time*time + time)/pow(1+ytm,time))
return (1/(presentvalue*pow(1+ytm,2))) * np.sum(temp)计算利率变化时的债券价格变动:
#计算利率变化时的债券价格变动
def calchange(duration,convexity,rchange,presentvalue):
return presentvalue*(-duration*rchange+0.5*convexity*rchange*rchange)调用函数进行计算:
mcd2205 = mcduration(cashflow,time_list,r_list,price2205)
dd2205 = dduration(cashflow,time_list,r_list,price2205)
conv2205 = Convexity(cashflow,time_list,price2205)
print("2205的麦考利久期是:",mcd2205,"\n2205的修正久期是:",dd2205,"\n2205的凸度是:",conv2205)
pvchange = calchange(dd2205,conv2205,0.01,price2205)
print("每期零利息率都增加100个基点后,债券价格的变动是:",pvchange)输出:
2205的麦考利久期是: 8.466388976332363 2205的修正久期是: 8.218457179826125 2205的凸度是: 81.77705143900583 每期零利息率都增加100个基点后,债券价格的变动是: -7.869522555177567