人工智能导论——遗传算法求解TSP问题实验

一、实验目的：

熟悉和掌握遗传算法的原理、流程和编码策略，并利用遗传算法求解组合优化问题，理解求解TSP问题的流程并测试主要参数对结果的影响。

二、实验原理：

旅行商问题，即TSP问题（Traveling Salesman Problem）是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路经的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个组合优化问题。该问题可以被证明具有NPC计算复杂性。因此，任何能使该问题的求解得以简化的方法，都将受到高度的评价和关注。

遗传算法的基本原理是通过作用于染色体上的基因寻找好的染色体来求解问题，它需要对算法所产生的每个染色体进行评价，并基于适应度值来选择染色体，使适应性好的染色体有更多的繁殖机会，在遗传算法中，通过随机方式产生 若干个所求解问题的数字编码，即染色体，形成初始种群；通过适应度函数给每 个个体一个数值评价，淘汰低适应度的个体，选择高适应度的个体参加遗传操作，经过遗产操作后的个体集合形成下一代新的种群，对这个新的种群进行下一轮的进化。本实验要求利用遗传算法求解TSP问题的最短路径。

三、实验内容：

1、参考实验系统给出的遗传算法核心代码，要求在相同的种群规模、最大迭代步数、独立运行次数下，用遗传算法求解不同规模（例如10个城市，30个城市，100个城市）的TSP问题，把结果填入表1。

表1 遗传算法求解不同规模的TSP问题的结果

城市规模	种群规模	最大迭代步数	独立运行次数	最好适应度	最差适应度	平均适应度	平均运行时间
10	100	100	10	25.1652	25.8521	25.3501	47s
30	100	100	10	10605.7	11868	11281.2	122.8s
100	100	100	10	44334.9	47149.1	46117.6	484.2s

1. 设置种群规模为100，交叉概率为0.8，变异概率为0.8，然后增加1种变异策略（例如相邻两点互换变异、逆转变异或插入变异等）和1种个体选择概率分配策略（例如按线性排序或者按非线性排序分配个体选择概率）用于求解30个城市的TSP问题（30个城市坐标如下），把结果填入表2。

30个城市坐标：

x[0]=41, x[1]=37,x[2]=54,x[3]=25,x[4]=7,x[5]=2,x[6]=68,x[7]=71,x[8]=54,x[9]=83;

y[0]=94,y[1]=84,y[2]=67,y[3]=62,y[4]=64,y[5]=99,y[6]=58,y[7]=44,y[8]=62,y[9]=69;

x[10]=64,x[11]=18,x[12]=22,x[13]=83,x[14]=91,x[15]=25,x[16]=24,x[17]=58,x[18]=71,x[19]=74;

y[10]=60,y[11]=54,y[12]=60,y[13]=46,y[14]=38,y[15]=38,y[16]=42,y[17]=69,y[18]=71,y[19]=78;

x[20]=87,x[21]=18,x[22]=13,x[23]=82,x[24]=62,x[25]=58,x[26]=45,x[27]=41,x[28]=44, x[29]=4;

y[20]=76,y[21]=40,y[22]=40,y[23]=7,y[24]=32,y[25]=35,y[26]=21,y[27]=26,y[28]=35; y[29]=50;

表2 不同的变异策略和个体选择概率分配策略的求解结果

变异策略	个体选择概率分配	最大迭代步数	独立运行次数	最好适应度	最差适应度	平均适应度	平均运行时间
两点互换	按适应度比例分配	100	10	889.434	982.154	938.503	59s
两点互换	按线性排序	100	10	488.833	567.304	513.735	51s
相邻两点互换变异	按线性排序	100	10	1022.77	1104.54	1064.78	49.1s
相邻两点互换变异	按适应度比例分配	100	10	878.549	969.802	939.414	58s

3、现给出中国 34 个省会数据，要求基于此数据设计遗传算法的改进算法解决该 TSP 问题。要求给出1）改进算法策略及核心代码，2）改进算法的主要参数设置（种群规模、交叉概率、变异概率、最大迭代步数等），3）改进算法最后求得的34 个省会的最短路径值、最优个体和算法运行时间，4）给出在相同的参数设置（种群规模、交叉概率、变异概率、最大迭代步数等）下，用基本遗传算法（没有使用改进策略）求得的34 个省会的最短路径值、最优个体和算法运行时间。

图 1  中国 34 省会位置(1295.72)

表3  34个省会城市及像素坐标表

城市	西藏	云南	四川	青海	宁夏	甘肃	内蒙古	黑龙江	吉林	辽宁	北京	天津
城市号	1	2	3	4	5	6	7	8	9	10	11	12
X坐标	100	187	201	187	221	202	258	352	346	336	290	297
Y坐标	211	265	214	158	142	165	121	66	85	106	127	135
城市	河北	山东	河南	山西	陕西	安徽	江苏	上海	浙江	江西	湖北	湖南
城市号	13	14	15	16	17	18	19	20	21	22	23	24
X坐标	278	296	274	265	239	302	316	334	325	293	280	271
Y坐标	147	158	177	148	182	203	199	206	215	233	216	238
城市	贵州	广西	广东	福建	海南	澳门	香港	台湾	重庆	新疆
城市号	25	26	27	28	29	30	31	32	33	34
X坐标	221	233	275	322	250	277	286	342	220	104
Y坐标	253	287	285	254	315	293	290	263	226	77

x[0]=100, x[1]=187,x[2]=201,x[3]=187,x[4]=221,x[5]=202,x[6]=258,x[7]=352,x[8]=346,x[9]=336;

y[0]=211,y[1]=265,y[2]=214,y[3]=158,y[4]=142,y[5]=165,y[6]=121,y[7]=66,y[8]=85,y[9]=106;

x[10]=290,x[11]=297,x[12]=278,x[13]=296,x[14]=274,x[15]=265,x[16]=239,x[17]=302,x[18]=316,x[19]=334;

y[10]=127,y[11]=135,y[12]=147,y[13]=158,y[14]=177,y[15]=148,y[16]=182,y[17]=203,y[18]=199,y[19]=206;

x[20]=325,x[21]=293,x[22]=280,x[23]=271,x[24]=221,x[25]=233,x[26]=275,x[27]=322,x[28]=250, x[29]=277;

y[20]=215,y[21]=233,y[22]=216,y[23]=238,y[24]=253,y[25]=287,y[26]=285,y[27]=254,y[28]=315; y[29]=293;

x[30]=286, x[31]=342,x[32]=220,x[33]=104;

y[30]=290,y[31]=263,y[32]=226,y[33]=77;

3.1结果：

3.1.1这边放了两个实验结果，区别仅是初始起点不同

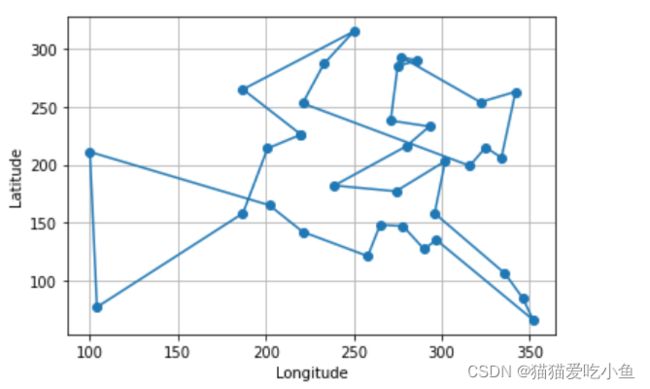
①绘制路径如图2（基于python，起点15）：

图2 绘图表示最优解

最短路径长度1532.3994414550848

路径表示：[23, 32, 24, 1, 2, 0, 33, 3, 5, 4, 12, 14, 16, 22, 21, 27, 31, 30, 26, 29, 28, 25, 20, 19, 18, 17, 13, 11, 9, 8, 7, 10, 6]

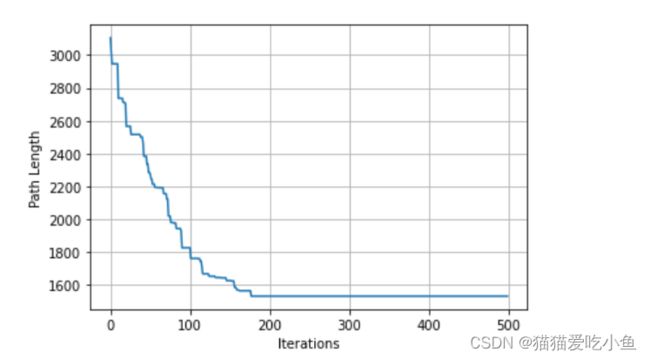
路径长度随着迭代次数下降：

图3 迭代次数和最优解关系

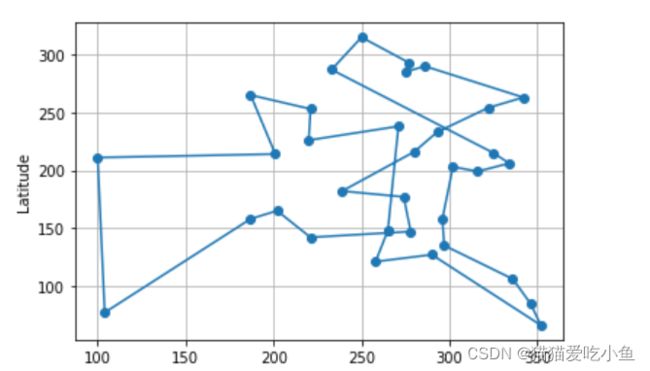
②绘制路径如图（基于python，起点32）：

图4绘图表示最优解

最短路径长度 ：1551.0699954694958

路径表示：[1, 28, 25, 24, 18, 20, 19, 31, 27, 29, 30, 26, 23, 21, 22, 16, 14, 17, 13, 9, 8, 7, 11, 10, 12, 15, 6, 4, 5, 0, 33, 3, 2]

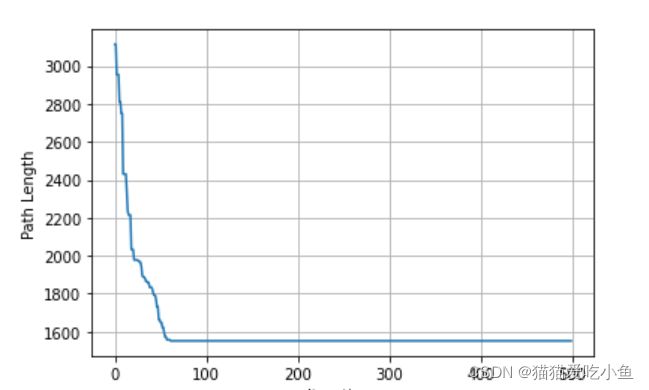
路径长度随着迭代次数下降：

图5最优解和迭代次数关系

3.1.2

若不改进，使用原先的程序，参数设置如下(基于C++)：

染色体长度:34

最大迭代步数:500

种群规模:100

交叉概率:0.5

变异概率0.15

选择操作：按适应度比例分配个体的选择概率，轮盘赌选择个体

交叉操作：PMX交叉

变异操作：相邻两点互换则

结果如图6：

图6结果

最优路径长度为： 6246.62

路径：32-20-18-21-28-29-26-24-13-30-12-10-31-33-2-3-1-7-9-4-15-11-0-5-8-6-17-16-23-25-19-22-27-14

运行时间为：214.6s

可见，改进算法还是比较很有效的。

3.2改进算法策略及核心代码：

①参数设定：
#种群数

count=300

#改良次数

improve_count=10000

#进化次数

itter_time=3000

#设置强者的定义概率，即种群前30%为强者

retain_rate=0.3

#设置弱者的存活概率

random_select_rate=0.5

#变异率

mutation_rate=0.1

②路径编码：

对城市进行编号0，1，2，3……33，染色体{x1,x2,x3....x33},表示从x1出发，依次经过x2,x3....x33再回到x1的路径，起点可任意设置，本程序中设为15.

③初始化种群：

为了加快程序的运行速度，在初始种群的选取中要选取一些较优秀的个体。先利用经典的近似算法—改良圈算法求得一个较好的初始种群。算法思想是随机生成一个染色体，比如{1，2，……33}，任意交换两城市顺序位置，如果总距离减小，则更新改变染色体，如此重复，直至不能再做修改。

代码：

#初始化种群

population = []

for i in range(count):

    # 随机生成个体

    x = index.copy()

    random.shuffle(x)

    improve(x)

    population.append(x)

#改良

def improve(x):

    i=0

    distance=get_total_distance(x)

    while i

        # randint [a,b]

        u=random.randint(0,len(x)-1)

        v = random.randint(0, len(x)-1)

        if u!=v:

            new_x=x.copy()

            t=new_x[u]

            new_x[u]=new_x[v]

            new_x[v]=t

            new_distance=get_total_distance(new_x)

            if new_distance

                distance=new_distance

                x=new_x.copy()

        else:

            continue

        i+=1

④选择策略：

虽然轮盘赌法是使用最多的选择策略 ,但这种策略可能会产生较大的抽样误差 所以，这采用自然选择，计算了每个城市之间的距离并存入了矩阵中，对总距离从小到大进行排序，选出适应性强的染色体，再选出适应性不强，但是幸存的染色体（随机选择）。

核心代码：

# 自然选择

def selection(population):

    # 对总距离从小到大进行排序

    graded = [[get_total_distance(x), x] for x in population]

    graded = [x[1] for x in sorted(graded)]

    # 选出适应性强的染色体

    retain_length = int(len(graded) * retain_rate)

    parents = graded[:retain_length]

    # 选出适应性不强，但是幸存的染色体

    for chromosome in graded[retain_length:]:

        if random.random() < random_select_rate:

            parents.append(chromosome)

    return parents

⑤变异策略：

按照给定的变异率，对选定变异的个体，随机地取三个整数，满足 1

核心代码：

#变异

def mutation(children):

    for i in range(len(children)):

        if random.random() < mutation_rate:

            child=children[i]

            u=random.randint(1,len(child)-4)

            v = random.randint(u+1, len(child)-3)

            w= random.randint(v+1, len(child)-2)

            child=children[i]

            child=child[0:u]+child[v:w]+child[u:v]+child[w:]

4、提交实验报告和源程序。

三、实验结果：

实验内容1结果：

表1 遗传算法求解不同规模的TSP问题的结果

城市规模	种群规模	最大迭代步数	独立运行次数	最好适应度	最差适应度	平均适应度	平均运行时间
10	100	100	10	25.1652	25.8521	25.3501	47s
30	100	100	10	10605.7	11868	11281.2	122.8s
100	100	100	10	44334.9	47149.1	46117.6	484.2s

实验内容2结果：

表2 不同的变异策略和个体选择概率分配策略的求解结果

变异策略	个体选择概率分配	最大迭代步数	独立运行次数	最好适应度	最差适应度	平均适应度	平均运行时间
两点互换	按适应度比例分配	100	10	889.434	982.154	938.503	59s
两点互换	按线性排序	100	10	488.833	567.304	513.735	51s
相邻两点互换变异	按线性排序	100	10	1022.77	1104.54	1064.78	49.1s
相邻两点互换变异	按适应度比例分配	100	10	878.549	969.802	939.414	58s

实验内容3结果，位于实验内容3中：

路径如图2：

最短路径长度1532.3994414550848

路径表示：[23, 32, 24, 1, 2, 0, 33, 3, 5, 4, 12, 14, 16, 22, 21, 27, 31, 30, 26, 29, 28, 25, 20, 19, 18, 17, 13, 11, 9, 8, 7, 10, 6]

四、实验思考及体会：

  1、分析遗传算法求解不同规模的TSP问题的算法性能。

城市规模越大，迭代数越大，搜索最优解的时间也越长，运行等待结果的时间越久。

2、增加1种变异策略和1种个体选择概率分配策略，比较求解30个城市的TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。

增加了相邻两点变异和线性排序选择个体：

变异策略：

void change1(vector& K, int N){//变异策略：相邻两点互换变异

int i = next_int() % N;

swap(K[i], K[(i + 1) % N]);

}

个体选择策略：

if(make_p==1)//线性排序

    {

        for(int i=0;i

ps[i]=(200-2*i)/popsize*(popsize+1);

}

从实验结果看，线性排序较好，随机两点交换策略明显优于相邻两点交换策略。

3、比较分析遗传算法的改进策略对求解34个城市的TSP问题的结果的影响。

主要是在适应值选择这块做了比较大的改进，优先选择了比较好的个体，又随机选择一部分差的个体，通过对一些参数和选择和变异等方面改进代码，可以使的想要获得的最优解更优，若不使用改进，最后运行可得的最优解在7.8千左右，如图7，精度远远不够。

 

图7 未改进运行结果

4.总结实验心得体会：

改进策略还有很多，例如：

①使用贪心算法初始化群体，每个个体生成的基本思想是:首先随机地从n个城市中选取- -个城市ccurrent作为第1个基因，然后从余下的n-1个城市中找到城市cnext (cnext 是距离ccurrent最近的城市)作为第2个基因，再从余下的n-2个城市中找到城市cnext+1 (cnext+1 是距离cnext最近的城市)作为第3个基因，依次类推，直到遍历n个城市为止。贪心算法生成的部分种群占比不大，在提高初始种群整体质量的同时，不会影响初始种群的多样性，有助于加速寻优速度。由于不是很熟悉代码，没能成功改成贪心算法初始化种群。

②还可以把适应度适当放大，考虑小数部分，但是从实验运行的结果看，意义并不大，最优解比较的一般，距离还是挺大的。

③改进交叉算子：基本遗传算法常用的双点交叉算子，这种交叉方式只是对父个体两点之间的基因进行交叉，两点区域外的基因要么不变，要么由于节点重复而盲目地改变，父个体的优良基因得不到有效继承。可以采用两点三段随机交叉。

未改进源码：

#include
#include
#include
#include
#include
#include
using namespace std;
typedef vector VI;
typedef vector VVI;
#define PB push_back
#define MP make_pair

int next_int()
{
	return rand()*(RAND_MAX+1)+rand();
}
double next_double()
{
	return (double(rand()*(RAND_MAX+1)+rand()))/((RAND_MAX+1)*RAND_MAX+RAND_MAX);
}
void pmx(VI& a,VI& b,int pointcnt)//PMX交叉
{
	int sa=next_int()%pointcnt,sb=next_int()%pointcnt;//随机选择两交叉位
	int temp;
	if (sa>sb)
	{
		temp=sa;
		sa=sb;
		sb=temp;
	}//保证交叉位sa<=sb
	VI aa(pointcnt),bb(pointcnt);
	int i;	
	for(i=0;isb))
			for (int j=sa;j<=sb;j++)
			{
				if(aa[i]==aa[j])  //有重复基因
				{  
					for(int k=0;ksb))
			for (int j=sa;j<=sb;j++)
			{	
				if(bb[i]==bb[j]) //有重复基因			
					bb[i]=v1tov2[bb[i]];	//进行互换				
			}
	
	}
	a=aa;
	b=bb;
	
}

vector x,y;
double fitness(const VI& v,int pointcnt)//计算适应度
{
	double r=0;
	for(int i=0;i& K,int N)//变异策略:两点互换
{
	int i=next_int()%N;
	int d=next_int()%(N-1);
	int j=(i+1+d)%N;
	swap(K[i],K[j]);
}


void change1(vector& K, int N){//变异策略：相邻两点互换变异 
	int i = next_int() % N;
	swap(K[i], K[(i + 1) % N]);	
}



void mutate(VI& route,int mutate_type,int pointcnt)
{
	
	if(mutate_type==0)//两点互换
		change0(route,pointcnt);	
	if(mutate_type==1)//相邻两点互换变异 
	    change1(route,pointcnt);
}



bool pair_dec(const pair& a,const pair& b)
{
	return a>b;
}

class other_population
{
public:
	int popsize,pointcnt;//种群规模,染色体长度
	double pc,pm;//交叉概率,变异概率
	vector >pop;//种群
	pair bestofpop;//最好个体
	int cross_type;//交叉类型
	int mutate_type;//变异类型
	int make_p;//个体概率分配策略类型
	int select_type;//个体选择类型
	int toursize;//竞赛规模
	double bestp;//最好个体选择概率
	other_population(int a,int b,int c,int f,int g,double d,double e,int h,double j,int m)
	{
		popsize=a,pointcnt=b,cross_type=c,mutate_type=f,make_p=g,pc=d,pm=e,toursize=h,bestp=j,select_type=m;
		for(int i=0;ibegin(),v->end());
			pop.PB(MP(fitness(*v,pointcnt),v));
		}
		sort(pop.begin(),pop.end(),pair_dec);
		bestofpop.first=pop[0].first;//初始时最好个体的适应度
		bestofpop.second=new VI(*pop[0].second);//初始时最好个体的染色体
	}
	~other_population()
	{
		for(int i=0;unsigned(i) ps(popsize);
		if(make_p==0) //按适应度比例分配个体的选择概率
		{
			double sum=0;
			for(int i=0;i > select_res;
			vector addsum(popsize);
			for(int i=0;i=0;i--)//进行变异
			if(next_double()1.0/gen.bestofpop.first)//更新最好适应度
		{
			best=1.0/gen.bestofpop.first;
			res=*gen.bestofpop.second;//存放最好个体的染色体
		}
		if(worst<1.0/gen.bestofpop.first)//更新最差适应度
			worst=1.0/gen.bestofpop.first;
		sum+=1.0/gen.bestofpop.first;//计算各次最好个体的适应度之和
	}
	cout << endl; 
	cout << CASNUM << "次遗传算法求解的结果如下：" << endl;
	clock_t	end_time=clock();
	double durTime=double(end_time-start_time);	
	sum/=CASNUM;//计算平均适应度
	cout<<"最好适应度："<