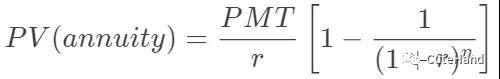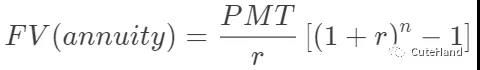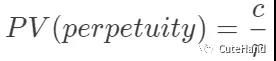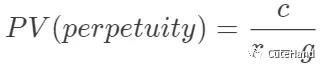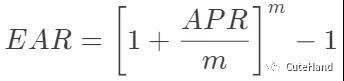【手把手教你】Python金融财务分析

内容来自：微信公众号：python金融量化
关注可了解更多的金融与Python干货。

内容目录

1. 货币时间价值
2. 年金计算
3. 实际利率
4. 项目投资分析
5. 单利与复利增长
   关于CuteHand

1. 货币时间价值

实际上numpy和scipy很强大，包含了计算各种财务指标的函数，可以直接调用，终值(fv)、现值(pv)、净现值(npv)、每期支付金额(pmt)、内部收益率(irr)、修正内部收益率(mirr)、定期付款期数(nper)、利率(rate)等等。

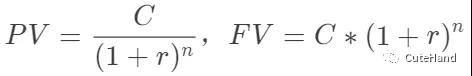
其中，PV为现值，FV为终值；C为现金流，r贴现率，n期限。

2. 年金计算

在n个时期内，每个时期可以获得等额现金流PMT，利率为r，以下是考试笔算时的公式：

普通年金现值：

普通年金终值：

永续债券现值：

其中，c为未来每期可以获得的现金收入，g是c的固定增长率。

年金计算比较简单，相当于等比数列求和。

#自定义计算一系列现金流现值（如年金）的函数
def pv_f(c,r,n,when=1):
    '''
    c代表每期现金流，可以每期不一样，
    如c=[100,90,80,120]，
    r贴现率，也可以每期不一样，如相应的，
    r=[2%,3%,2%,4%]，
    n为期数，
    when=1表示期末计数，默认，即普通年金
    when=0表示期初计数，即预付年金
    '''
    import numpy as np  #导入numpy库
    c=np.array(c)       
    r=np.array(r) 
    if when==1:
        n=np.arange(1,n+1)
    else:
        n=np.arange(0,n)
    pv=c/(1+r)**n
    return pv.sum()

应用实例1： 有个五年的普通年金年金，每年可获得20000元，假设贴现率为5%，现值是多少？
扩展：如果是预付年金呢？

c=20000
r=0.05
n=5
#调用前文定义的函数pv_f(c,r,n,when=1)
pv1=pv_f(c,r,n,when=1)
print("普通年金现值（年末）：%.2f"% pv1)
#如果是预付年金，则when=0
pv2=pv_f(c,r,n,when=0)
print("预付年金现值（年初）：%.2f" % pv2)
普通年金现值（年末）：86589.53
预付年金现值（年初）：90919.01
#使用上2.年金计算公式验证下我们自定义函数是否正确
pv1=20000/0.05*(1-1/(1+0.05)**5)
print("使用计算公式计算（年末）：
      {:.2f}" .format(pv1))
pv2=20000/0.05*(1-1/(1+0.05)**5)*(1+0.05)
print("使用计算公式计算（年初）：
      {:.2f}" .format(pv2))
#使用numpy自带函数验证
import numpy as np
print("numpy自带公式计算（年末）：{:.2f}
     ".format(np.pv(r,5,-c),when=0))
print("numpy自带公式计算（年初）：{:.2f}
      ".format(np.pv(r,5,-c,when=1))) 
#结果一致
使用计算公式计算（年末）：86589.53
使用计算公式计算（年初）：90919.01
numpy自带公式计算（年末）：86589.53
numpy自带公式计算（年初）：90919.01

如果要计算一系列现金流的终值呢？

#自定义终值函数
def fv_f(c,r,n,when=1):
    import numpy as np  
    c=np.array(c)     
    r=np.array(r)      
    if when==1:
        n=sorted(np.arange(0,n),
        reverse=True) #注意n与pv里的n不一样
    else:
        n=sorted(np.arange(1,n+1),
        reverse=True)
    fv=c*(1+r)**n
    return fv.sum()

#可以将二者合成一个函数，直接输出现值和终值
def pv_fv(c,r,n,when=1,fv=0): 
    '''
    c,r,n参数同上；
    when用来判断期初还是期末现金流，默认期末
    fv判断求现值还是终值，默认是现值
    '''
    import numpy as np  
    c=np.array(c)     
    r=np.array(r) 
    if fv==0:
        if when==1:
            n=np.arange(1,n+1)
        else:
            n=np.arange(n)
        pv=c/(1+r)**n
        return pv.sum()
    else:
        if when==1:
            n=sorted(np.arange(0,n),
              reverse=True) 
        else:
            n=sorted(np.arange(1,n+1),
               reverse=True)
        fv=c*(1+r)**n
        return fv.sum()

应用实例2：未来五年年末分别收到100、200、300、100、500元，每年贴现率分别为4%、5%、6%、8%和10%，求现值和终值。

c=[100,200,300,100,500]
r=[0.04,0.05,0.06,0.08,0.10]
n=5
pv1=pv_f(c,r,n)    #默认when=1可不写
pv2=pv_fv(c,r,n)   #默认when=1，fv=0，
fv1=fv_f(c,r,n)    #统一函数下
fv2=pv_fv(c,r,n,fv=1) #统一函数下
print("现值：%.2f元； %.2f元" % (pv1,pv2)) 
print("终值：%.2f元； %.2f元" % (fv1,fv2)) 
现值：913.41元； 913.41元
终值：1293.59元； 1293.59元

已知现值或终值，利率和时期，求每期支出或收入现金流呢？

#定义一个计算每期现金流的函数
def pmt(r,n,pv=0,fv=0,when=1):
    import numpy as np
    pv=np.array(pv)
    fv=np.array(fv)
    r=np.array(r)
    if fv==0:
        if when==1:
            n=np.arange(1,(n+1))
        else:
            n=np.arange(n)
        pv_pmt=pv/(1/(1+r)**n).sum()
        return pv_pmt

    else:
        if when==1:
            n=sorted(np.arange(0,n),
               reverse=True) 
        else:
            n=sorted(np.arange(1,n+1),
              reverse=True)
        fv_pmt=fv/((1+r)**n).sum()  
            #知道终值求每期现金流
        return fv_pmt

应用实例3：假设向某银行贷款200万元买房，贷款利率5.0%，按月还款，30年还清本息，请问每月应该还多少钱？

pv=2000000
r=0.05/12  
n=30*12
pmt1=pmt(r,n,pv)  #套用上面公式
#numpy自带公式计算
pmt2=np.pmt(r,n,pv,fv=0,when='end') 
print("自定义函数计算：%.2f元" % pmt1)
print("numpy自带公式计算：%.2f元"% pmt2)  
#负号代表现金流支出
自定义函数计算：10736.43元
numpy自带公式计算：-10736.43元

应用实例3扩展：假设计息利率调整一次，前15年利率保持5%，后15年利率上调到6%。可以理解为：假设前15年每月按照10736元还款，后15年如果利率上升到6%，应该每月还多少？

c0=10736
n0=n1=15*12
r0=0.05/12
r1=0.07/12
pv0=pv_f(c0,r0,n0)   #每月还10736,还15现值
pv1=pv-pv0           #还完15年后剩余还款现值
pv2=pv1*(1+0.05)**15 #转化成15年后的终值
pmt1=pmt(r1,n1,pv2)  #以6%利率接着还剩下的15年
print("后15年每年应还款金额：%.2f元" % pmt1)
后15年每年应还款金额：12003.44

应用实例4：假设计划15年后要给小孩准备一笔300万元的留学资金，投资收益率为8%，请问从现在开始每月需要投入多少钱？

fv=3000000
r=0.08/12
n=15*12
#使用自定义公式
pmt1=pmt(r,n,fv=fv,when=0)
#使用numpy自带公式
pmt2=np.pmt(r,n,pv=0,fv=fv,when='begin')  
print("自定义函数计算：%.2f元" % pmt1)
print("numpy自带公式计算：%.2f元"% pmt2)  
#可见如果每年投资收益率可以达到8%，
#每月只需投资8612.15元，15年后就可以收到300万元啦
#问题是普通工人大众很难持续获得8%/年的投资收益率，
#一般是放银行定期，5年以上5%以内
pmt3=pmt(0.05/12,n,fv=fv,when=0)
#每月投资支出增加
p=(pmt3-pmt1)/pmt1
print("假设利率为5%情况：{0:.2f}元,
每月支出增加比例：{1:.2f} %".format(pmt3,p*100))
#如果考虑通货膨胀，实际也没多少收益率了
自定义函数计算：8612.15元
numpy自带公式计算：-8612.15元
假设利率为5%情况：11177.24元,
每月支出增加比例：29.78 %

3. 实际利率

其中，EAR为实际年利率（effective annual rate)；AP为名义年利率(Annual Percentage Rate)；m是一年内复利的频率。

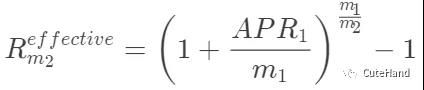
连续复利（Continuously compounded interest rate）

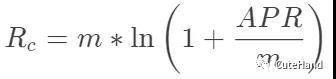
知识回顾
名义利率与实际利率跟通胀率对应的名义利率不同。实际利率是什么呢？

情景一：年初存入银行100块钱，银行承诺利率12%。于是年末能拿到112块钱。这里的12块钱就是利息，12%就是实际利率。
情景二：年初存入银行100块钱，银行承诺利率12%。聪明的人发现一个漏洞（假设半年就是12%/2），银行承诺12%，也就是半年利率可记为6%。然后当存入100块半年后，取出来106块钱，接着转身去另一个柜员处存入106块半年，期末将得106*（1+6%）=112.36白白多得3毛6。这里的实际利率就是12.36%。
情景三：年初存入银行100块钱，银行承诺利率12%。更加聪明的人把100块钱存取了三次，就是100*（1+4%）^3=112.4864比聪明的人还多得1毛2分6厘4。此时的实际利率是12.4864%。
【这里银行承诺的就是名义利率，而实际所得的是实际利率。（当然现实生活中的商业银行会把半年利率调低，而不是单纯的用一年的利率除以期数。）而后面两种情景的计息方式为 复利。俗称利滚利。不要以为利滚利就能滚上天，有一个条件限制住了它，叫名义利率。随着存取次数的不断增加，每一个期数内的利率也在逐渐减小。现在把计息次数扩大到∞，实际利率就变成了（1+12%/∞）^{∞，而这玩意计算出来就是e}12%。这就是所谓的连续复利。】

4. 项目投资分析

金融财务分析里关于项目投资分析判断的方法有很多，比较常用的有净现值、回收期、内部收益率法等。

净现值法 （Net present value,NPV）

项目投资NPV法判断依据：

def npv_f(rate,cashflows):
    total=0.0
    for i, cashflow in enumerate(cashflows):
        total+=cashflow/(1+rate)**i
    return total

回收期法（Payback period）

与净现值法相比，优点是简单易懂，缺点：

不考虑时间价值

基准回收期的确定比较主观

内部收益率法（IRR）
IRR：使得净现值为0的贴现率。

def IRR_f(cashflows,interations=10000):
    rate=1.0
    inv=cashflows[0]
    for i in range(1,interations+1):
        rate*=(1-npv_f(rate,cashflows)/inv)
    return rate

应用实例5：假设贴现率为5%，有A、B两个项目，前期均需投入120万， A项目第一年至五年分别收入10、30、50、40、10万，而项目B第一至五年分别收入30、40、40、20、10万，项目A和B哪个投资价值高？

#分析：如果光从金额看都是投资120万元，
#回报都是140万元，
#从回收期法来看，二者都是在第四年才收回成本
#但由于货币的时间价值，下面从净现值的角度进行分析
r=0.05
C_A=[-120, 10, 30, 50, 40, 10]
C_B=[-120, 30, 40, 40, 20, 10]
npv_A=npv_f(r,C_A)
npv_B=npv_f(r,C_B)
print("项目A的净现值：%.2f万元" % npv_A)
print("项目B的净现值：%.2f万元" % npv_B)
项目A的净现值：0.67万元
项目B的净现值：3.70万元
#内部收益率法比较
irr_A=IRR_f(C_A,interations=10000)
irr_B=IRR_f(C_B,interations=10000)
print("项目A的内部收益率：%.2f%%" % (irr_A*100))
print("项目B的内部收益率：%.2f%%" % (irr_B*100))
项目A的内部收益率：5.19%
项目B的内部收益率：6.28%

NPV与IRR比较

NPV：优点：计算相对简便易懂，结果直观，容易理解；局限性：没有消除初始投资额不同的差异，也没有消除投资项目期限的差异。

IRR：优点：跟NPV比较消除了初始投资额不同和项目投资期限的差异，直观反映项目本身的报酬率；缺点是计算量大，可能存在多解或无解。

净现值和内部收益率适用范围不同，净现值适用于互斥方案间的择优，而内部收益率用于独立方案间的择优。

应用实例6：有项目C、D，一次性投入均为100万元，其中，C项目前六年无现金流入，第7年现金流入200万；D项目前六年每年现金流入12万，最后一年现金流入112万，选择哪个？

C=[-100,0,0,0,0,0,200]
D=[-100,12,12,12,12,12,112]
irr_C=IRR_f(C)*100
irr_D=IRR_f(D)*100
print("内部收益率：C项目{0:.0f}%,D项目
    {1:.0f}%" .format(irr_C,irr_D))
print("净现值：C项目{0:.2f}万元，D项目
    {1:.2f}万元".format(npv_f(0.1,C),
    npv_f(0.1,D)))
#请问你会选哪一个呢？
内部收益率：C项目12%,D项目12%
净现值：C项目12.89万元，D项目8.71万元
#应用实例6扩展1
E=[-100,90,50,0,0,10]
F=[-100,0,0,0,0,350]
irr_E=IRR_f(E)*100
irr_F=IRR_f(F)*100
print("内部收益率：E项目{0:.0f}%,F项目
  {1:.0f}%" .format(irr_E,irr_F))
print("净现值：E项目{0:.2f}万元，F项目
  {1:.2f}万元".format(npv_f(0.1,E),
   npv_f(0.1,F)))
#你又会选哪一个呢？
内部收益率：E项目31%,F项目28%
净现值：E项目29.35万元，F项目117.32万元
#应用实例6扩展2
G=[-100,90,50,0,0,10]
H=[-150,0,50,50,50,150]
irr_G=IRR_f(E)*100
irr_H=IRR_f(F)*100
print("内部收益率：G项目{0:.0f}%，H项目
  {1:.0f}%".format(irr_G,irr_H))
print("净现值：G项目{0:.2f}万元，H项目
  {1:.2f}万元".format(npv_f(0.1,G),
  npv_f(0.1,H)))
#你又会选哪一个呢？
内部收益率：G项目31%，H项目20%
净现值：G项目29.35万元，H项目56.18万元

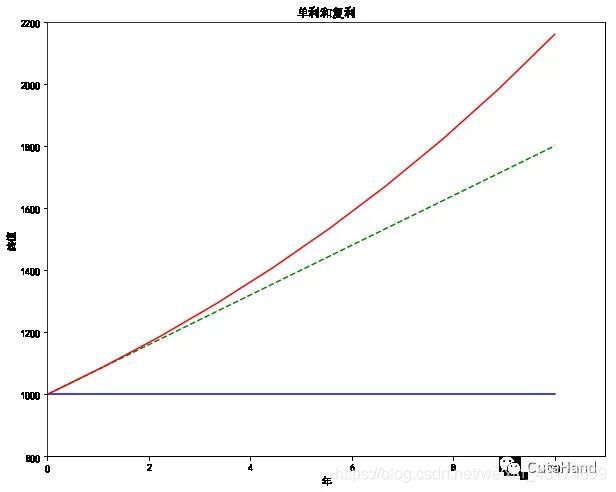
5. 单利与复利增长

#单利和复利
import numpy as np
%matplotlib inline
from matplotlib import pyplot as plt
#解决中文乱码
from pylab import mpl  
mpl.rcParams['font.sans-serif'] = ['SimHei'] 

pv=1000
r=0.08
n=10
t=np.linspace(0,n,n)
y1=np.ones(len(t))*pv  
y2=pv*(1+r*t)
y3=pv*(1+r)**t
plt.figure(figsize=(10,8))
plt.title('单利和复利')
plt.xlabel('年')
plt.ylabel('终值')
plt.xlim(0,11)
plt.ylim(800,2200)
plt.plot(t,y1,'b-')
plt.plot(t,y2,'g--')
plt.plot(t,y3,'r-')