人工智能导论——Prolog编程求解图搜索问题(代码实现)
人工智能导论实验报告
Prolog编程求解图搜索问题
- 一、 实验目的
- 二、 实验的硬件、软件平台
- 三、 实验内容及步骤
-
- 1. 实验内容:
-
- 【问题描述】
- 【问题分析】
- 2. 实验步骤:
-
- 2.1. 安装prolog集成开发环境
- 2.2. 采用prolog编写所选问题的源程序
- 2.3. 编译程序,输出查询问题的结果或数据
- 3. 画出状态空间图:
- 四、 问题与分析
-
- 1. 直接使用write打印表结构无法输出所有路径
- 2. 逆序输出
- 五、 总结
- 六、 附录
-
- 1. 事实与规则
- 2. 查询语句
- 3. 查询结果
一、 实验目的
- 熟悉PROLOG的运行环境,进行PROLOG的基本编程练习;
- 了解PROLOG语言中常量、变量的表示方法。PROLOG的简单程序结构,掌握分析问题、询问解释技巧;进行事实库、规则库的编写,并在此基础上进行简单的询问。
- 求解图搜索问题。
实际应用题目:传教士与野人问题
二、 实验的硬件、软件平台
硬件:计算机
软件:操作系统:WINDOWS
应用软件:SWI-Prolog
三、 实验内容及步骤
1. 实验内容:
熟悉prolog语言的使用并实现求解图搜索问题——传教士与野人过河问题;
【问题描述】
有 N 个传教士和 N 个野人来到河边渡河,河岸有一条船,每次至多可供 k 人乘渡。问:传教士为了安全起见,应如何规划摆渡方案,使得任何时刻, 河两岸以及船上的野人数目总是不超过传教士的数目(否则不安全,传教士有可能被野人吃掉)。 即求解传教士和野人从左岸全部摆渡到右岸的过程中,任何时刻满足 M (传教土数) ≥ C (野人数)和 M+C≤k 的摆渡方案。
【问题分析】
假设以传教士和野人的数量N为3,船一次最大的载人量K为2进行分析。
初始状态:河左岸有3个野人河3个传教士;河右岸有0个野人和0个传教士;船停在左岸,船上有0个人。
目标状态:河左岸有0个野人和0个传教士;河右岸有3个野人和3个传教士;船停在右岸,船上有0个人。
2. 实验步骤:
2.1. 安装prolog集成开发环境
Prolog是门奇特的编程语言,在人工智能领域中,常用于建立专家系统、自然语言处理等。由于SWI-Prolog提供了相对丰富的功能和完善的环境,所以在这里我选择它作为Prolog的编程环境。
SWI-Prolog在官网进行下载后安装,过程较为简单,因此省略;
安装成功后打开软件进入界面:
此时可以进行源程序的编写,通过【File】-【new …】新建pl文件,编写源程序;
2.2. 采用prolog编写所选问题的源程序
对该问题的程序设计分为五个部分:
-
设计问题的状态
首先需要使用Prolog的数据结构来表达两岸的状态(传教士、野人数量、小船所在位置);
用如下复合结构来表达问题的某个状态:
((左岸传教士数,左岸野人数),(右岸传教士数,右岸野人数),船的位置)
船的位置为0表示船在左岸,为1表示在右岸,一开始,所有的人与船都在右岸;
因此,初始状态为:((0,0),(3,3),1),目标状态为:((3,3),(0,0),0);
当然,实际上是没有必要包括两个岸上的人数的,因为一个岸上的人数可以通过总人数减去另一岸上的人数来算出,不过这里写出两个岸上的人数便于理解。 -
描述可能的动作
船上所载人的方案就是可能的动作,这里用谓词move表示;
move(x,y),表示船上载x个传教士、y野人,x+y<2;
根据要求,共得出以下5中可能的动作:①. 渡2传教士 —— move(2,0)
②. 渡2野人 —— move(0,2)
③. 渡1野人1传教士 —— move(1,1)
④. 渡1传教士 —— move(1,0)
⑤. 渡1野人 —— move(0,1) -
判断合法状态
除了上面状态的数据结构以及移动的谓词move外,还需要判断一个状态是否合法的推理;
用表达式legal((X,Y,))来表示状态(X,Y,)是否合法,‘’表示匿名变量,即不考虑该参数的值,在我们定义的状态中,该参数表示船的位置,与合法性无关,因此我们不考虑它;

当legal_an(X),legal_an(Y)为真时,状态legal((X,Y,))为真;
而legal_an(X),表示对于某一岸X岸上传教士、野人的人数是否合法;
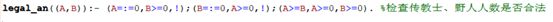
如代码所示,legal_an((A,B))为真的条件是,岸上全是传教士、岸上全是野人、或岸上传教士人数大于等于野人数;
左右两岸上的人数都合法,那么当前的状态合法,但是它并不判断左右两岸的人数之和是否正确,即((2,1),(1,1),0)对于legal来说也是为真的,不过在后面的程序中会避免这种情况出现,因此也不需要进行人数之和的检查; -
状态的转移
使用nextstatu(Statu,Statu1)表达式来进行Statu到Statu1的状态转移,它需要三个过程,

move谓词有5种取值使其为真,即五种渡河选择;
update(Statu,(X,Y),Statu1)就是根据move来进行状态的转移,它的推理方式如下:

注意:这里的if_then_else函数是自己实现的条件语句,其推理如下:
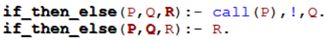
这里if__then_else有三个参数,当第一个参数P为真时,如果Q为真那么if_then_else表达式为真,否则第一个参数P不为真时,R为真时if_then_else表达式为真。
因此,update所做的就是根据Q是否为0(船的位置)以及move的选择,来进行左右两岸的(传教士,野人)的数目的增加或减少,新的状态计入Statu1中;
最后通过legal表达式来判断新的状态Statu1是否合法;
至此就完成了状态的转移,临近的新状态的生成。 -
深度优先搜索
主要依靠如下表达式实现深搜:
findroad(X,Y,L),X表示当前状态,Y表示目标状态,这里Y应该是不变的,L是从初始状态到达目标状态所保存的路径表。

同样用到了条件语句,如果X=Y,那么说明找到了目标状态,进行打印的操作,这里因为在深搜的过程中表中的顺序是反的因此需要先进行一个逆序的过程,建立一个表LN保存L的逆序,然后打印LN(通过show函数);

逆序的操作较为简单,直接调用reverse函数即可实现,但是这里需要注意不能改变原来的表L,因为表L变化会影响到回溯后的下一中方案的查询(可能有多种渡河方案);
如果X!=Y那么if_then_else第三个参数必须为真才能使表达式为真,第三个参数为:(nextstatu(X,Z),not(member(Z,L)),findroad(Z,Y,[Z|L])),即首先找到一个满足条件的下一状态Z,判断Z是否在L中,不在为真,则将Z加入到表L中,以Z为当前状态再次进行深搜;
- 过程的打印
上面提到对过程表LN的打印依靠show(LN)函数;

show(L)主要依靠了迭代的方式来顺序打印L表中的每一个元素;
首先找到L表中的第一个元素A(通过first函数)以及除去A后的表B(通过last函数);
将A打印出来后,对B表继续show(B)的过程;
first、last实现方法如下:

2.3. 编译程序,输出查询问题的结果或数据
将上述程序保存到’cjs.pl’文件中后,在SWI-Prolog的命令行中打开

为true表示成功;
接下来用?-语句进行查询,即
findroad(((0,0),(3,3),1),((3,3),(0,0),0),[((0,0),(3,3),1)])语句进行初始状态到目标状态的路径查询,L表初始化含有初始状态;
结果如下:

共找到四条路径;
3. 画出状态空间图:
(x,y,c)表示左岸的传教士人数、野人人数、船的位置(省略右岸状态)

即,有四条路径,与输出结果相同。
四、 问题与分析
1. 直接使用write打印表结构无法输出所有路径

如图,在找到路径时如果直接打印表,即write(L),会出现如下结果:

即,只打印了一条路径就返回了;
write()是打印命令。命令本身就是一个表达式,输出完成以后,返回值就是true。
因此,如果这里使用write的话在X=Y时(找到目标状态后),第二个参数所有语句为真,那么findroad(X,Y,L)就会为真,一层层回溯到最顶层的查询语句就是真,搜索直接结束,因此这里不能简单的使用write;
【解决方法】
如我的代码所示,使用迭代实现的show表达式:
![]()
show就是一个一个的打印表中的元素,在最后,它的第一个参数length一定会为假(表空),所以会迭代返回false,导致findroad中的show的返回值为false,因此会一直搜索直到搜索所有的情况,并且最后打印false(这里指的是findroad的三个参数全部都无法返回真值true)。
2. 逆序输出
在一开始,如果对得到的表L直接打印,那么会打印出一个逆序的过程(因为是逆序加入的表);

运行出来是逆序的;

【解决方法】
因此这里我加入了nx表达式,将L逆序得到新表LN,打印LN,这里nx直接调用prolog函数:
![]()
相对解决方法较为简单。
五、 总结
第一次接触prolog语言,不得不说这个语言十分有趣,能通过它进行一些推理,甚至可以实现递归、迭代、搜索算法等等操作。
在Prolog的程序的运行流程方面我有了如下的认识:规则的运行是通过Prolog内建的回溯功能实现的、我们可以使用内部谓词fail来强制实现回溯、我们也可以通过加入一条参数为伪变量(下划线)无Body部分的子句,来实现强制让谓词成功。数据库中的事实代替了一般语言中的数据结构。回溯功能能够完成一般语言中的循环操作。而通过模式匹配能够完成一般语言中的判断操作。规则能够被单独地调试,它和一般语言中的模块相对应。而规则之间的调用和一般语言中的函数的调用类似。
当然,这次实验也稍有一些不足,传教士与野人问题是可以进行一个扩展到一般性情况的问题,这里因时间原因只写出了它的传教士、野人数目确认的情况,后面尝试去求解它的一般性情况。
这次实验非常的有趣,受益匪浅。
六、 附录
1. 事实与规则
move(1,0).
move(0,1).
move(0,2).
move(2,0).
move(1,1).
legal((X,Y,_)):-
legal_an(X),
legal_an(Y).
legal_an((A,B)):- (A=:=0,B>=0,!);(B=:=0,A>=0,!);(A>=B,A>=0,B>=0).
update((X,Y,Q),Move,Statu):-(A,B)=X, (C,D)=Y,(E,F)=Move,
if_then_else(
Q=:=0, %Q == 0
(C1 is C+E, D1 is D+F, A1 is A-E, B1 is B-F, Statu=((A1,B1),(C1,D1),1)),
(C1 is C-E, D1 is D-F, A1 is A+E, B1 is B+F, Statu=((A1,B1),(C1,D1),0))
).
nextstatu(Statu,Statu1):- %
move(X,Y),
update(Statu,(X,Y),Statu1),
legal(Statu1).
if_then_else(P,Q,R):- call§,!,Q.
if_then_else(P,Q,R):- R.
nx(X,Y):- reverse(X,Y).
first(A,X):- append([A],_,X). %AX
last(B,X):- first(A,X),append([A],B,X). %
show(L):-if_then_else((length(L,X),X>0), %LX>0
(first(A,L),last(B,L),write(’[’),write(A),write(’]’),nl,show(B)),
fail). %
findroad(X,Y,L):-
if_then_else(X=Y,
(write(’------------’),nl,nx(L,LN),show(LN),nl), %nxL
(nextstatu(X,Z),not(member(Z,L)),findroad(Z,Y,[Z|L]))). %ZL
2. 查询语句
?- findroad(((0,0),(3,3),1),((3,3),(0,0),0),[((0,0),(3,3),1)]).
3. 查询结果
[(0,0),(3,3),1]
[(0,2),(3,1),0]
[(0,1),(3,2),1]
[(0,3),(3,0),0]
[(0,2),(3,1),1]
[(2,2),(1,1),0]
[(1,1),(2,2),1]
[(3,1),(0,2),0]
[(3,0),(0,3),1]
[(3,2),(0,1),0]
[(2,2),(1,1),1]
[(3,3),(0,0),0]
[(0,0),(3,3),1]
[(0,2),(3,1),0]
[(0,1),(3,2),1]
[(0,3),(3,0),0]
[(0,2),(3,1),1]
[(2,2),(1,1),0]
[(1,1),(2,2),1]
[(3,1),(0,2),0]
[(3,0),(0,3),1]
[(3,2),(0,1),0]
[(3,1),(0,2),1]
[(3,3),(0,0),0]
[(0,0),(3,3),1]
[(1,1),(2,2),0]
[(0,1),(3,2),1]
[(0,3),(3,0),0]
[(0,2),(3,1),1]
[(2,2),(1,1),0]
[(1,1),(2,2),1]
[(3,1),(0,2),0]
[(3,0),(0,3),1]
[(3,2),(0,1),0]
[(2,2),(1,1),1]
[(3,3),(0,0),0]
[(0,0),(3,3),1]
[(1,1),(2,2),0]
[(0,1),(3,2),1]
[(0,3),(3,0),0]
[(0,2),(3,1),1]
[(2,2),(1,1),0]
[(1,1),(2,2),1]
[(3,1),(0,2),0]
[(3,0),(0,3),1]
[(3,2),(0,1),0]
[(3,1),(0,2),1]
[(3,3),(0,0),0]
false.