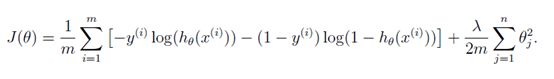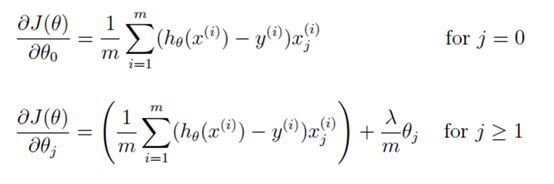非线性逻辑回归（2维至28维特征映射+正则化）及Python源码

一、问题引入

在上次的博文中说了二分类中的线性逻辑回归问题，我们可以将两类数据通过一条简单的直线进行“分割”。但实际上，逻辑回归中的数据并不一定是那么“规矩”的排列，也就是很多情况下两类数据的边界并不那么规整，我们无法通过一条简单的直线对数据进行分类，这类问题即为“非线性逻辑回归问题”。接下来，我将通过吴恩达课后题的例子为大家提供自己解决“非线性回归问题”的思路及源代码。其中包括特征映射、正则化、决策边界划分的概述。

题目要求如图1.1所示。

图1.1 问题描述

 

 

二、特征映射

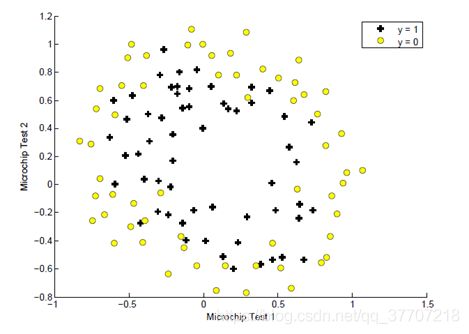
基于上述题目说一下自己对特征映射的浅见，首先我们先看一下数据集的分布及特征数量，如图2.1所示。

图 2.1 训练集分布图

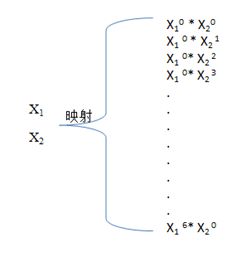
通过上图可以看出，两类数据的决策边界形状类似圆形，并且数据集中仅仅提供了两个特征（实际上，当特征数大于3时，训练集就不满足可视化了）。我们无法通过两个特征来训练出一条复杂的决策边界，这就用到了从低维到高维的“特征映射”。在本题目中，所谓特征映射就是将已知两个特征的各阶幂级数的乘积组合作为新的特征。在本题中，我们将2维度特征映射为了28维特征。具体映射方式如图2.2所示。

图2.2 特征映射

 

 

三、正则化

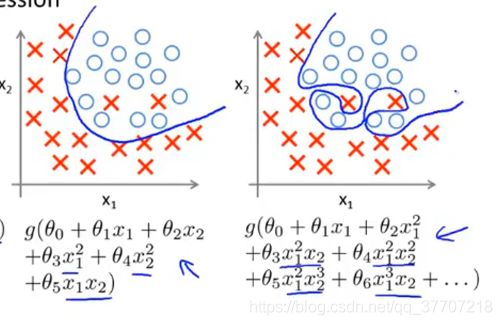
在进行特征映以后，新增特征中就出现了很多原始特征的高阶项，而高阶项的出现则可能导致“过拟合”问题。如图3.1所示。

图3.1 “过拟合”对比图

通过对比上述两图可以很明显看出，左图是对数据集更好的分界，而右图虽然决策边界将训练集完全的分为了两部分，但训练出的决策边界是明显不符合实际的，右图即为典型的“过拟合”。在过拟合中，假设函数会“不择手段”的去降低代价函数值，因此过拟合中，代价函数通常很低甚至为0。过拟合问题的是由假设函数中的高阶项导致的，而本题中恰好有很多高阶项，这也就是要在该题中运用正则化的原因。正则化的思路是，既然过拟合问题是由高阶项引起的，那么就让高阶项前面的参数尽可能的小，这样就可以减少高阶项对整个假设函数的影响，以抑制过拟合问题。控制高阶项前参数的方式为，给这些参数加“惩罚项”。加上惩罚项后的代价函数如图3.2所示。

图3.2 正则化后的代价函数

上图中，最后的那一项即为“惩罚项”，其中的lamd为正则化参数，它代表了“惩罚力度”。因为在很多例子中，我们实现无法事先知道哪一项是高阶项，因此只能对除theta0之外的所有theta进行无差别惩罚（在假设函数中，theta0是与1相乘的，因此对theta0惩罚作用不大）。因为惩罚项正是与各项相乘的参数组成的，在迭代中，代价函数值要想尽量小即必须使参数尽量小，这样一来也就减弱了高阶项对假设函数的影响，防止过拟合。

因为代价函数发生了变化，，因此其偏导随之变化，如图3.3所示。

图3.3 代价函数的偏导形式

 

 

四、等高线画决策边界

决策边界类似圆形，传统的“取点连线”的方式已经完全不适用，因为在圆形中，x与y并非“一一对应”，可能是1对0、1对1、1对多。因此，本题的决策边界采用等高线来画更为方便。在平面取一些点，然后算出每个点的等高值，最后画出等高值为0的那条等高线，那就是我们要求的决策边界。

 

 

五、Python源码

（本想讲一下代码实现思路，但由于矩阵操作用文字很难描述清楚，就不写了，可以留言讨论。对于“逻辑回归中假设函数的形式是咋来”的可以查看我的上一篇博文、对于“梯度下降算法的原里”可以查看我上上篇博文）

###1.导入需要的宏包
import pandas as pd
import numpy as np
import math
from sympy import *
import matplotlib.pyplot as plt



###2.数据预处理：读出数据并按列取出方便后续特征映射
data=pd.read_csv('E:\Exercises\code_myself\ex2\\ex2data2.txt',sep=',',header=None,names=['test1','test2','result']) #读出文件中的数据(默认为datdaframe数据帧)
x1=np.matrix(data.test1).T
x2=np.matrix(data.test2).T
Y=np.matrix(data.result).T



###3.特征映射(对矩阵)函数定义：进行特征映射并做相关处理
def Featuremapping(x1,x2):
	i=0
	j=0
	k=0 
	while i<=6:
		while j<=6-i: 
			data[format(k)]=np.multiply(np.power(x1,i),np.power(x2,j)) #特征映射过程中对dataframe的列名进行重命名，以方便引用
			j+=1
			k+=1
		j=0
		i+=1
	del data['test1'] #将原始的三列删除
	del data['test2']
	del data['result']
	return data

	

###4.计算代价函数
def Costfunction(X,Y,theta,lamd):
	Z=np.dot(X,theta.T)
	h=1/(1+np.exp(-Z)) #求出h矩阵
	first=sum(np.multiply(Y,np.log(h))) #求初始代价值J
	second=sum(np.multiply((1-Y),np.log(1-h)))
	reg=(lamd/(2*len(Y)))*sum(np.power(theta[1:,:],2))
	J=(-1/len(Y))*(first+second)+reg
	return J
	
	
###5.对数值(x,y)进行特征映射,以供计算等高线值
def Value_mapping(x,y):
	value=np.matrix(np.ones((1,28)))
	i=0
	j=0
	k=0 
	while i<=6:
		while j<=6-i: 
			value[0,k]=np.power(x,i)*np.power(y,j)
			j+=1
			k+=1
		j=0
		i+=1
	return value
	

	
###6.梯度下降算法
def Gradientdescent(X,Y,theta,alpha,lamd,iters):
	temp = np.matrix(np.zeros(theta.shape)) #构建零值矩阵
	parameters = int(theta.ravel().shape[1])# ravel计算需要求解的参数个数 功能将多维数组降至一维
	cost=np.zeros(iters) #构建iters个0的数组，用来储存代价值
	for i in range(iters):
		Z=np.dot(X,theta.T) 
		h=1/(1+np.exp(-Z)) 
		error=h-Y
		#先对“不惩罚项theta0进行更新”
		term=np.multiply(error,X[:,0])#计算两矩阵(hθ(x)-y)x
		temp[0,0] = theta[0,0]-((alpha/len(Y)) * np.sum(term))
		#对其他矩阵theta中的其他theta_i进行更新
		for j in range(1,parameters): #theta0已经单独更新，因此接下来的更新从theta1开始
			term=np.multiply(error,X[:,j])+ (lamd/len(Y))*theta[0,j]   #计算两矩阵(hθ(x)-y)x+(lamd/m)*theta_j
			temp[0,j]=theta[0,j]-((alpha/len(Y))*np.sum(term))   
		theta=temp
		cost[i]=Costfunction(X,Y,theta,lamd) 
	return theta, cost


	
###7.把原数据集记性特征映射，初始化X、theta、alpha、iters、lamd;执行梯度下降函数
data=Featuremapping(x1,x2) #特征映射
X=np.matrix(data) #初始化X
theta=np.matrix(np.ones((1,28))) 
alpha=5 #学习率
iters=100 #迭代次数
lamd=1 #正则化参数
g,cost=Gradientdescent(X,Y,theta,alpha,lamd,iters)



###8.画图
data2=pd.read_csv('E:\Exercises\code_myself\ex2\\ex2data2.txt',sep=',',header=None,names=['test1','test2','result']) #用作最后画点
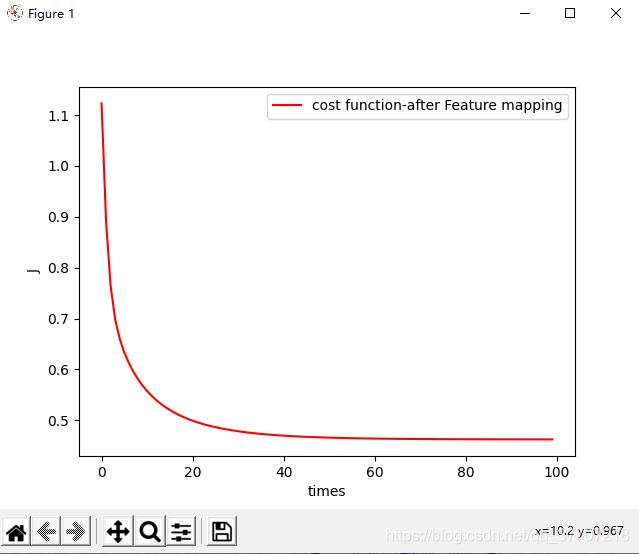
##(1)画代价函数图
plt.figure()
plt.xlabel('times')
plt.ylabel('J')
plt.plot(np.arange(iters),cost,'-r',label='cost function-after Feature mapping')
plt.legend()  #给图像加图例，图例格式默认

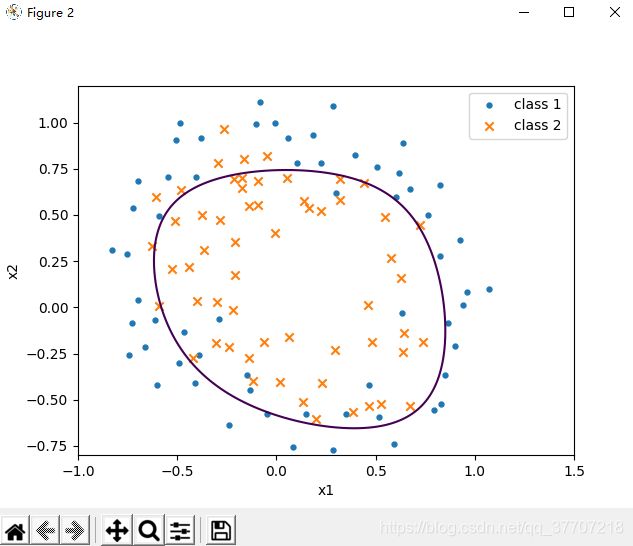
##(2)画训练集图与决策边界
plt.figure() #画训练集图
plt.xlabel('x1')
plt.ylabel('x2')
plt.xlim(-1,1.5)
plt.ylim(-0.8,1.2)
plt.scatter(data2.test1[data2.result==0],data2.test2[data2.result==0],s=np.pi*2**2,label='class 1') #画结果为0的点
plt.scatter(data2.test1[data2.result==1],data2.test2[data2.result==1],marker='x',label='class 2') #画结果为1的点 

i=0 #画决策边界图
j=0
l=np.matrix(np.zeros((200,200)))
m1=(np.linspace(-1,1,200)).reshape(200,1)
n1=(np.linspace(-1,1,200)).reshape(200,1)	
m,n= np.meshgrid(m1,n1)

while i<200:
	while j<200: 
		l[i,j]=np.dot(Value_mapping(m1[i],n1[j]),g.T)
		j+=1
	j=0
	i+=1	
	
plt.contour(m,n,l,[0])
plt.legend()  #给图像加图例，图例格式默认
plt.show()

 

 

六、运行结果

图6.1  代价函数

图6.2 决策边界

 

 

 

左肩理想右肩担当，君子不怨永远不会停下脚步！