LR-GCCF:让GCN更深
LR-GCCF:让GCN更深
1 一点点引入
在读 ‘Revisiting Graph based Collaborative Filtering: A Linear Residual Graph Convolutional Network Approach’ 摘要时,就感觉文中提出的LR-GCCF和LightGCN的思路有异曲同工之妙!于是查了查两篇文章的发表时间,都是2020年。只不过LightGCN专注于探讨简化之后的NGCF是不是会得到更好的表现,而LR-GCCF除了简化embedding更新机制外,还把注意放到了如何将GCN层堆地更深。
准备好了吗,下面我们来看看LR-GCCF是怎么样的吧!
不了解LightGCN小伙伴戳下面的链接简单过一遍呀~
LightGCN不相信非线性激活与特征转换
2 LR-GCCF一瞥
2.1 非线性激活是必要的吗?
LR-GCCF与LightGCN一样,都是属于基于图神经网络的协同过滤算法。熟悉LightGCN的小伙伴可能都有印象,LighGCN之所以敢把非线性激活函数和线性特征转换移除,是因为LightGCN的输入是user和item的ID,没有关于user和item的特征信息,因此非线性激活函数和线性特征转换是没有用武之地的。就好像让小汽车在狭窄的弄堂里穿梭,还不如用走的。
LR-GCCF移除非线性激活函数的原因其实和LightGCN类似。原因在于LR-GCCF的初始embedding也是要通过训练生成的,不包含额外的特征信息,这个看文章给出的源代码即可:
class BPR(nn.Module):
def __init__(self, user_num, item_num, factor_num,user_item_matrix,item_user_matrix,d_i_train,d_j_train):
super(BPR, self).__init__()
"""
user_num: number of users;
item_num: number of items;
factor_num: number of predictive factors.
"""
self.user_item_matrix = user_item_matrix
self.item_user_matrix = item_user_matrix
self.embed_user = nn.Embedding(user_num, factor_num)
self.embed_item = nn.Embedding(item_num, factor_num)
for i in range(len(d_i_train)):
d_i_train[i]=[d_i_train[i]]
for i in range(len(d_j_train)):
d_j_train[i]=[d_j_train[i]]
self.d_i_train=torch.cuda.FloatTensor(d_i_train)
self.d_j_train=torch.cuda.FloatTensor(d_j_train)
self.d_i_train=self.d_i_train.expand(-1,factor_num)
self.d_j_train=self.d_j_train.expand(-1,factor_num)
nn.init.normal_(self.embed_user.weight, std=0.01)
nn.init.normal_(self.embed_item.weight, std=0.01)
def forward(self, user, item_i, item_j):
users_embedding=self.embed_user.weight
items_embedding=self.embed_item.weight
gcn1_users_embedding = (torch.sparse.mm(self.user_item_matrix, items_embedding) + users_embedding.mul(self.d_i_train))#*2. #+ users_embedding
gcn1_items_embedding = (torch.sparse.mm(self.item_user_matrix, users_embedding) + items_embedding.mul(self.d_j_train))#*2. #+ items_embedding
gcn2_users_embedding = (torch.sparse.mm(self.user_item_matrix, gcn1_items_embedding) + gcn1_users_embedding.mul(self.d_i_train))#*2. + users_embedding
gcn2_items_embedding = (torch.sparse.mm(self.item_user_matrix, gcn1_users_embedding) + gcn1_items_embedding.mul(self.d_j_train))#*2. + items_embedding
gcn3_users_embedding = (torch.sparse.mm(self.user_item_matrix, gcn2_items_embedding) + gcn2_users_embedding.mul(self.d_i_train))#*2. + gcn1_users_embedding
gcn3_items_embedding = (torch.sparse.mm(self.item_user_matrix, gcn2_users_embedding) + gcn2_items_embedding.mul(self.d_j_train))#*2. + gcn1_items_embedding
# gcn4_users_embedding = (torch.sparse.mm(self.user_item_matrix, gcn3_items_embedding) + gcn3_users_embedding.mul(self.d_i_train))#*2. + gcn1_users_embedding
# gcn4_items_embedding = (torch.sparse.mm(self.item_user_matrix, gcn3_users_embedding) + gcn3_items_embedding.mul(self.d_j_train))#*2. + gcn1_items_embedding
gcn_users_embedding= torch.cat((users_embedding,gcn1_users_embedding,gcn2_users_embedding,gcn3_users_embedding),-1)#+gcn4_users_embedding
gcn_items_embedding= torch.cat((items_embedding,gcn1_items_embedding,gcn2_items_embedding,gcn3_items_embedding),-1)#+gcn4_items_embedding#
user = F.embedding(user,gcn_users_embedding)
item_i = F.embedding(item_i,gcn_items_embedding)
item_j = F.embedding(item_j,gcn_items_embedding)
# # pdb.set_trace()
prediction_i = (user * item_i).sum(dim=-1)
prediction_j = (user * item_j).sum(dim=-1)
# loss=-((rediction_i-prediction_j).sigmoid())**2#self.loss(prediction_i,prediction_j)#.sum()
l2_regulization = 0.01*(user**2+item_i**2+item_j**2).sum(dim=-1)
# l2_regulization = 0.01*((gcn1_users_embedding**2).sum(dim=-1).mean()+(gcn1_items_embedding**2).sum(dim=-1).mean())
loss2= -((prediction_i - prediction_j).sigmoid().log().mean())
# loss= loss2 + l2_regulization
loss= -((prediction_i - prediction_j)).sigmoid().log().mean() +l2_regulization.mean()
# pdb.set_trace()
return prediction_i, prediction_j,loss,loss2
因此,文章的作者认为非线性激活会让模型训练的复杂度增加,对于协同过滤推荐算法来说,非线性激活函数也许是可以去除的。
具体地,给定user-item矩阵 A = ( R 0 N × M 0 M × N R T ) A=\begin{pmatrix} {\bf R} & {\bf 0}^{N \times M} \\ {\bf 0}^{M \times N} & {\bf R}^T\end{pmatrix} A=(R0M×N0N×MRT),假设初始embedding为 E 0 ∈ R ( M + N ) × D {\bf E}^0 \in {\bf R}^{(M+N)\times D} E0∈R(M+N)×D,其中 E 0 [ 1 : M , : ] {\bf E}^0[1:M,:] E0[1:M,:]为user的embedding的矩阵块, E 0 [ M + 1 : M + N , : ] {\bf E}^0[M+1:M+N,:] E0[M+1:M+N,:]为item的embedding的矩阵块。
第 k k k层的embedding矩阵 E k {\bf E}^k Ek由以下公式得到:
E k = S E k W k {\bf E}^k = {\bf S} {\bf E}^k {\bf W}^k Ek=SEkWk
其中, S = D ^ − 0.5 A ^ D ^ − 0.5 {\bf S}={\bf \hat{D}^{-0.5} \hat{A} \hat{D}^{-0.5}} S=D^−0.5A^D^−0.5, A ^ = A + I \bf \hat{A} = A+I A^=A+I, D ^ \bf \hat{D} D^为矩阵 A ^ \bf \hat{A} A^的度矩阵, W k {\bf W}^k Wk为第 k k k层的参数。
2.2 GCN怎么做得更深
GCN通常堆两层,原因在于:两层的GCN其实就可以将网络中大部分节点的特征信息聚合到目标节点身上。如果再深一点,每个节点聚集特征的对象就会大量重复,导致训练出来的embedding区分能力比较弱。于是作者做了一个实验,见下图:
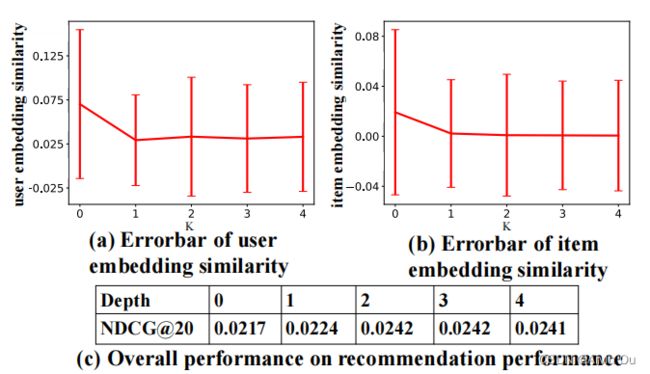
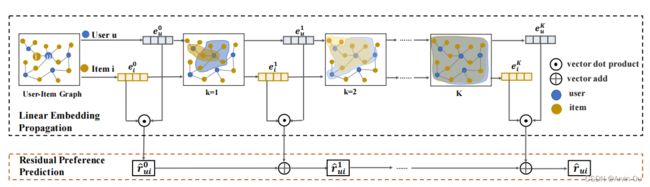
可以看到, k k k从0到2性能是提升的,但是超过2之后就没有任何提升了。为了突破这一瓶颈,LR-GCCF参考了ResNet,在模型中引入了跳连接。跳连接示意图如下:

其中, r ^ u i 0 = < e u 0 , e i 0 > \hat{r}^0_{ui}=
2.3 损失函数
LR-GCCF同样使用BPR损失,公式如下:
m i n Θ L B P R = ∑ a = 1 M ∑ ( i , j ) ∈ D a − l n ( s ( r ^ a i − r ^ a j ) ) + λ ∣ ∣ Θ 1 ∣ ∣ 2 {\bf min}_\Theta L_{BPR}=\sum_{a=1}^M\sum_{(i,j)\in D_a}-ln(s(\hat{r}_{ai}-\hat{r}_{aj}))+\lambda||\Theta_1||^2 minΘLBPR=a=1∑M(i,j)∈Da∑−ln(s(r^ai−r^aj))+λ∣∣Θ1∣∣2
其中, s ( x ) s(x) s(x)为sigmoid激活函数, Θ = [ Θ 1 , Θ 2 ] \Theta=[\Theta_1,\Theta_2] Θ=[Θ1,Θ2], Θ 1 = E 0 \Theta_1=\bf E^0 Θ1=E0, Θ 2 = { W k , k = 1 , 2... , K } \Theta_2=\{{\bf W}^k, k=1,2...,K\} Θ2={Wk,k=1,2...,K}。
3 效果如何
首先,作者对比了baseline模型,效果见下表: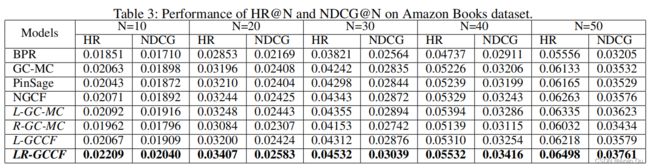
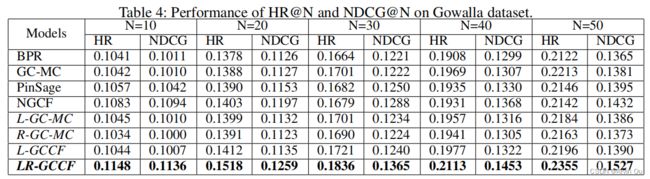
可以看到,在Amazon和Gowalla数据集上LR-GCCF的表现比所有baseline要好。其中L-GCCF为没有跳连接的LR-GCCF。
接着,测试了不同深度的LR-GCCF表现:
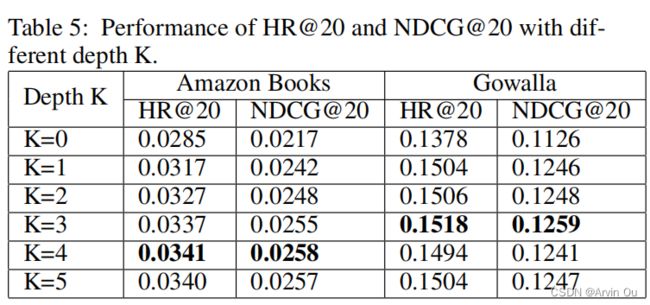
最后,对比了L-GCCF和LR-GCCF的表现:
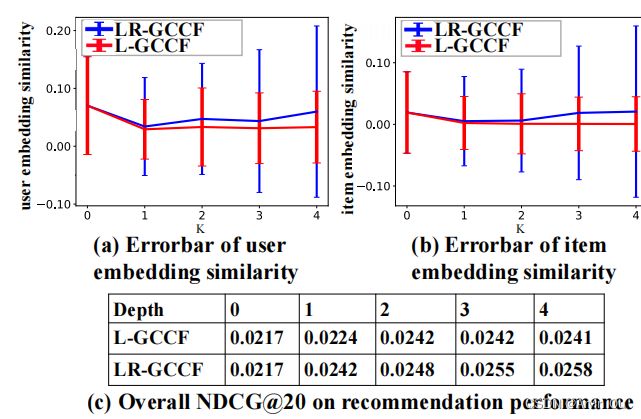
可以看到,GCN确实可以堆得更深了,但是具体还是要随数据集调整。
4 总结
读完LR-GCCF,个人有以下几点思考(不一定对):
- GCN之所以做不深,和网络的连边密度有关。比如,在连边比较稠密的网络中,每个节点的三阶邻居其实就已经有很多重复的邻居。此时,根据GCN的传播机制,每个节点聚合到的信息会存在大量的重复,从而导致生成的embedding表示能力较差。如果这个推断是正确的话,那么理论上来说我们通过把网络变得稀疏一点(比如删除冗余连边)就可以把GCN做得更深。但删边带来的信息损失和更深GCN带来的增益又该如何权衡?
- LR-GCCF和LightGCN之所以剔除非线性激活,是因为模型的输入没有包含节点特征,需要模型自己学到初始embedding。相对于Multi-GCCF,前两个算法的效率比较高,但可解释性方面我觉得看得还是有点云里雾里。
参考资料
- Revisiting Graph based Collaborative Filtering: A Linear Residual Graph Convolutional Network Approach
- LR-GCCF github