【记录】传统的医学图像增强方法

基于hessian矩阵的特定形状增强滤波器

hessian矩阵图像中表示当前点的二阶导矩阵；一阶导表示灰度的变化，二阶导是变化的变化，即灰度的曲率。

求解出hessian矩阵的特征向量，可以将该点的曲率进行分解。特征值最大对应的特征向量方向表示该点的主曲率方向。不同形状的物体，其有着不同的曲率特征，比如：

（1）3D管状结构，两个垂直的方向上曲率很大（横切血管的平面上的两个正交方向），沿着血管方向的曲率小；特征值中，两个很大，一个约为0；（vesselness filter）

（2）3D片状结构，片面内的两个垂直方向曲率很小（~=0），垂直于片的方向曲率很大。特征值中，一个很大，两个约为0；（sheetness filter）

（3）3D球状结构，三个垂直方向曲率都大，三个特征值应该都挺大；（blobness filter）

（4）其他…

利用以上的特征值的，就可以针对不同的形状进行增强。

另外，还要考虑物体的不同尺度，通常会采用多尺度的思想，就是对图像先做一个高斯滤波，滤波器的方差，表示尺度，从而实现可以检测不同尺度的物体，如不同粗细的血管、不同薄厚的板子，不同大小的球等等。

这一类增强处理，放在深度学习之前，或者和原图并一起输入，对于目标的检测或分割应该只有好处没有坏处。

直方图均衡 Histogram equalization

概述

直方图均衡是在方法的图像处理的对比度使用调整图像的直方图。直方图均衡是增强图像的最佳方法。它提供了更好的图像质量，而不会丢失任何信息。

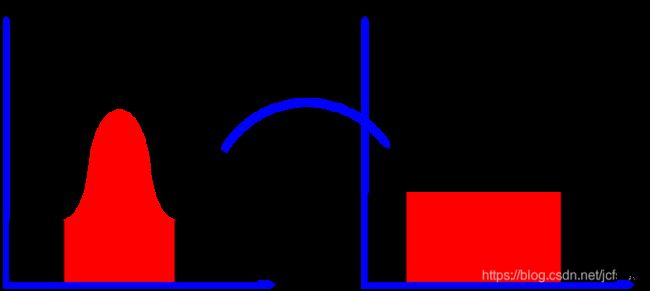
这种方法通常会提高许多图像的整体对比度，尤其是当图像的可用数据由接近的对比度值表示时。通过此调整，强度可以更好地分布在直方图上。这允许较低局部对比度的区域获得较高对比度。直方图均衡通过有效分散最频繁的强度值来实现。

该方法在背景和前景都亮或都暗的图像中很有用。特别地，该方法可以导致在X射线图像中更好地查看骨骼结构，并在曝光过度或曝光不足的照片中获得更好的细节。该方法的主要优点是它是一种相当简单的技术，并且是可逆的运算符。因此，从理论上讲，如果已知直方图均衡函数，则可以恢复原始直方图。该计算不是计算密集型的。该方法的缺点是它是不加区别的。可能会增加背景噪音的对比度 ，同时减少可用信号。

在科学成像中，空间相关性比信号强度（例如，分离量化长度的DNA片段）更重要，通常较小的信噪比会妨碍视觉检测。

直方图均衡化经常在照片中产生不切实际的效果；但是，对于科学图像（例如热图像，卫星图像或X射线图像），通常是与伪色相同的图像类别，它非常有用。当应用于低色彩深度的图像时，直方图均衡化也会产生不良影响（例如可见图像梯度）。例如，如果应用于以8 位灰度调色板显示的8位图像，它将进一步减小图像的色深（唯一的灰色阴影数量）。当应用于色深更高的图像时，直方图均衡化效果最佳而不是调色板大小，例如连续数据或16位灰度图像。

有两种方法可以考虑和实现直方图均衡化，即图像更改或调色板更改。该操作可以表示为P（M（I）），其中I是原始图像，M是直方图均衡映射操作，P是调色板。如果我们将新调色板定义为P’= P（M）并保持图像I不变，则直方图均衡化将作为调色板更改来实现。另一方面，如果调色板P保持不变，并且图像被修改为I’= M（I），则实现方式是通过图像更改。在大多数情况下，调色板更改会更好，因为它可以保留原始数据。

此方法的修改使用多个直方图（称为子直方图）来强调局部对比度，而不是整体对比度。这种方法的示例包括自适应直方图均衡，对比度限制自适应直方图均衡或CLAHE，多峰直方图均衡（MPHE）和多用途Beta优化双直方图均衡（MBOBHE）。这些方法（尤其是MBOBHE）的目标是通过修改HE算法来提高对比度，而不会产生亮度均值偏移和细节损失伪像。

在生物神经网络中似乎也发生了与直方图均衡等效的信号变换，以便根据输入统计量最大化神经元的输出触发率。这已在飞行果蝇 视网膜中得到了证明。

直方图均衡化是直方图重映射方法中更为通用的一类。这些方法试图调整图像以使其更易于分析或改善视觉质量（例如retinex）

实现

考虑一个离散的灰度图像 { x }，令n i为灰度i的出现次数。图像中出现第i级像素的概率为

$$p_x(i)=p(x=i)=\frac{n_i}{n},0\le i<L$$

L是图像中灰度的总数（通常为256），n是图像中像素的总数，并且{\ displaystyle p_ {x}（i）}p_ {x}（i） 实际上是像素值i的图像直方图，已标准化为[0,1]。

我们还定义了累积分布函数对应p X为

$$cd{f}_x(i)=\sum _{j=0}^i{p}_x(x=j)$$

这也是图像的累积归一化直方图。

我们想创建一个形式为y = T（x）的转换，以生成具有平坦直方图的新图像{ y }。这样的图像将在整个值范围内具有线性化的累积分布函数（CDF），即

$$cd{f}_y(i)=iK$$

对于某一常数ķ。CDF的属性使我们能够执行这样的变换（请参阅逆分布函数）；它被定义为

$$cd{f}_y(y^{\prime })=cd{f}_y(T(k))=cd{f}_x(k)$$

其中k在[0，L]范围内）。注意，由于我们使用归一化的直方图{x}，因此T将级别映射到[0,1]范围内。为了将值映射回到其原始范围，需要对结果应用以下简单转换：

$$y^{\prime }=y\cdot (max\{x\}-min\{x\})+min\{x\}$$

这里提供了更详细的推导。

例子

为了与统计用法保持一致，应将“ CDF”（即累积分布函数）替换为“累积直方图”，尤其是因为该文章链接到通过将累积直方图中的值除以像素总数而得出的累积分布函数。均衡CDF的等级定义为rank/pixelcount.

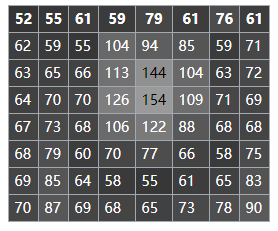
所示的8位灰度图像具有以下值：

以8位灰度显示的8×8子图像

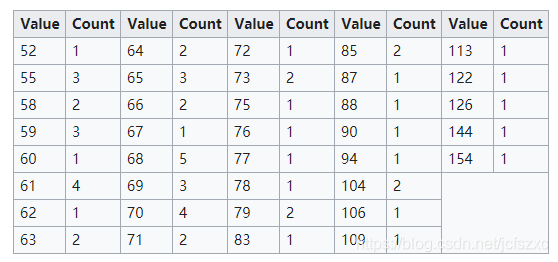
下表中显示了该图像的直方图。为了简洁起见，排除了具有零计数的像素值。

所述累积分布函数（CDF）如下所示。再次，为简洁起见，排除了不会增加cdf的像素值。

此cdf显示子图像中的最小值为52，最大值为154。值154的cdf为64，与图像中的像素数一致。CDF必须标准化为[0,255]。直方图的一般均衡公式为：

$$h(v)=round(\frac{cdf(v)-cd{f}_{min}}{(M\times N)-cd{f}_{min}}\times (L-2)+1)$$

其中cdf（v）>0。从1缩放到255保留最小值的非零值。

示例比例数据从0到255（包括0和255）的均衡公式为：

$$h(v)=round(\frac{cdf(v)-1}{63}\times 255)$$

例如，78的cdf为46。（第7列的下一行使用78的值。）标准化后的值变为

$$h(78)=round(\frac{46-1}{63}\times 255)=round(0.714286\times 255)=182$$

完成此操作后，将直接从归一化的cdf中获取均衡图像的值以产生均衡值：

请注意，最小值（52）现在为0，最大值（154）现在为255。

应用于图片：

自适应直方图均衡 Adaptive histogram equalization

概述

直方图均衡虽然可以显著改善图像质量，但是它是一个全局修改的方法——图像的每一个像素值都用完全相同的变换函数来修改。这样做的弊端在于图像局部的细节很可能因为受到其他区域的属性的影响而丢失。例如在下图的高亮度区域，全局直方图均衡调整之后，由于亮度过高而呈现一片亮白，很难再看清楚海豹的细节纹理。

原图：

直方图均衡后

既然全局调整效果不太理想，一个直接的想法就是进行局部调整。将图片分成若干区域，每个区域单独进行直方图均衡操作，这样各个区域就不会受到其他区域的影响而导致细节丢失了。显然，这个方法的也不是完美的。由于各个区域采用了不同的变换函数，在相邻区域的边界处的像素值在处理后几乎不可能保持连续性——只有在每个区域各自的直方图都完全一致的情况下才有可能保持连续性，而这显然和实际情况不符。

解决这个问题的办法其实也很简单，既然是由于采用了不同的变换函数而导致的不连续性，那就对变换函数插值使得最终的变换函数在整个图像上是连续的就好了(Wiki)。插值的方法跟图像双线性插值是一样的，只要将变换函数想象成一个图像就好了。把每个小区域内的变换函数想象成一个像素点，这些变换函数共同构成了一副小图像，而原图像的像素点则相当于这个小图像内的亚像素元素(sub-pixel elements)。在进行直方图均衡操作时，原图的每个像素点的变换函数由它所在的区域以及周围三个相邻区域的变换函数插值得到。插值的时候考虑该像素点离这四个区域中心的距离并以此为权重进行线性插值。如下图所示，红色像素点的变换函数T由T1, T2, T3和T4插值得到：

T = T1 * (1-fx) * (1-fy) + T2 * fx * (1-fy) + T3 * (1-fx) * fy + T4 * fx * fy

因为直方图均衡的变换函数本身也是线性的,所以上面的公式可以直接改写成：

k = 255 / n * [ c1(I) * (1-fx) * (1-fy) + c2(I) * fx * (1-fy) + c3(I) * (1-fx) * fy + c4(I) * fx * fy ]

其中c1, c2, c3, c4分别为这四个区域的累积分布函数, I是红色像素点的亮度值。

处理完之后效果如下，相比于全局直方图均衡来说，自适应直方图均衡的很好地保留了局部的细节信息，而且还增强了图像的纹理。但是也可以看到图像中的背景噪声相应的被放大了。

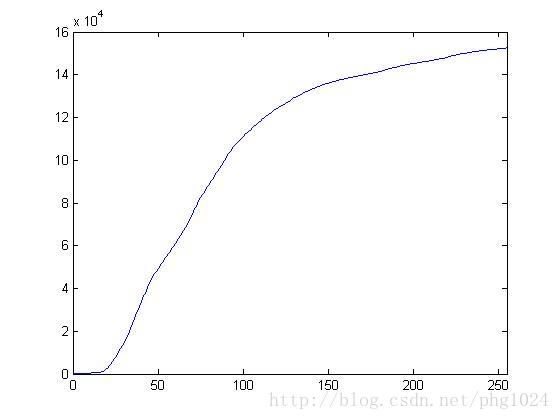
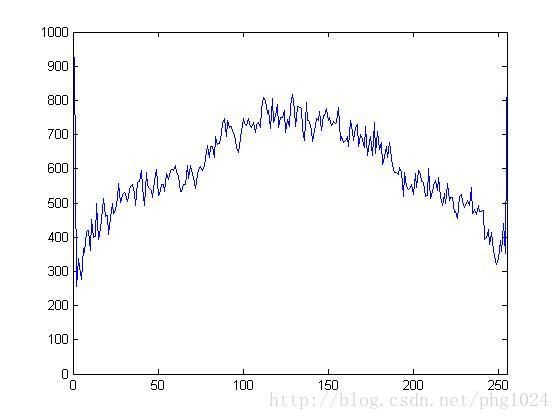
这个方法处理过后的图像直方图也是近似线性的，但是因为考虑了图像的局部特性，一部分高亮度的像素点并没有映射到很高的亮度上，而且有一部分低亮度的像素点也没有映射到很低的亮度值，所以整个曲线呈现轻微的S形。

原图	直方图均衡	自适应直方图均衡
		)

而图像的亮度分布则显著的变均匀了

原图	直方图均衡	自适应直方图均衡

再来看看其他图片的效果

原图	直方图均衡	自适应直方图均衡

参考博客1

参考博客2

CLAHE

概述

普通的AHE往往会放大图像近恒定区域中的对比度，因为此类区域中的直方图高度集中。结果，AHE可能导致噪声在近恒定区域中被放大。对比度受限AHE（CLAHE）是自适应直方图均衡的一种变体，其中对比度放大受到限制，从而减少了这种噪声放大问题。

在CLAHE中，给定像素值附近的对比度放大由变换函数的斜率给出。这与邻域累积分布函数（CDF）的斜率成比例，因此与该像素值处的直方图的值成比例。CLAHE通过在计算CDF之前将直方图裁剪为预定值来限制放大。这限制了CDF的斜率，从而限制了转换函数的斜率。直方图被裁剪的值，即所谓的裁剪极限，取决于直方图的规格化，并因此取决于邻域的大小。公共值将结果放大倍数限制在3到4之间。

有利的是，不丢弃直方图超出裁剪限制的部分，而是在所有直方图块中平均分配它。

重新分配将使某些容器再次超过剪辑限制（图中绿色阴影区域），从而导致有效的剪辑限制大于规定的限制，其确切值取决于图像。如果这是不希望的，则可以递归地重复重新分配过程，直到可以忽略不计。

paper链接

参考博客

混合空间增强

鸡尾酒疗法。

嗯，我觉得这一节是轻松娱乐的一节。因为不用引入新的知识，知识把我们之前讲的内容杂糅一下就可以了。

比如，我们之前学过了高斯模糊、梯度锐化、拉普拉斯锐化，所有的这些都是作为单一的知识点介绍的。但是在成人的世界里，哪有这么多的完美模型可以用一种方法解决？这就需要集中方法顺序地使用，这样才能达到最优的效果。

举个例子：

从左到右，从上到下依次为a) b) c) d)

从左到右，从上到下依次为e) f) g) h)

a) 原图：全身骨骼扫描图像

b) 图a经过拉普拉斯变化后的结果

c) 将a图 + b图的锐化结果

d) 图a经过Sobel锐化后的结果

e) 对d进行5*5 均值滤波器平滑后的结果

f) c和e相乘得到的掩蔽图像

g) a和f求和后得到的锐化图像

h) 对图g进行幂变换得到的最终结果

参考知乎

非锐化掩模 Unsharp masking

锐化遮罩（USM）是一种图像锐化技术，通常在数字图像处理软件中可用。其名称源于以下事实：该技术使用模糊的或“不清晰”的负像来创建原始图像的蒙版。[1] 然后，将不清晰的蒙版与原始的正像合并，以创建比原始的模糊少的图像。生成的图像虽然更清晰，但可能无法准确表示图像的对象。在信号处理的上下文中，不清晰的蒙版通常是线性的或非线性的 放大信号高频分量的滤波器。

降噪+自适应权重retinex+灰度映射

在混合空间增强的步骤中，加入了USM的方法，效果提升明显。

锐化蒙版应用于图像的下部

对于照相暗室处理，将大幅面玻璃底片底片接触复印到低对比度的胶片或底片上以产生正像。但是，使用与复印件背面接触的复印材料进行正复印，而不是使用乳剂对乳剂进行复印，因此它变得模糊不清。处理后，该模糊的正片将与原始负片的背面接触而被替换。当光线同时通过负片和套准正片（例如在放大仪中）通过时，正片会部分抵消负片中的某些信息。

由于正值已被故意模糊，因此仅低频（模糊）信息被消除。此外，遮罩可有效减小原始负片的动态范围。因此，如果将得到的放大图像记录在对比相纸上，则部分消除会强调原稿中的高空间频率信息（精细细节），而不会丢失高光或阴影细节。所得到的印刷品看起来比没有钝化面具的印刷品更加锐利：其敏锐度得到了提高。

在摄影过程中，可以通过更改用于初始不清晰掩模曝光的光源的“柔度”或“硬度”（从点光源到完全漫射）来控制模糊量，而效果的强度可以是通过更改不清晰蒙版的对比度和密度（即曝光和显影）来控制。

对于传统摄影，通常在单色材料上使用不清晰的蒙版。特殊的全色软加工黑白胶片可用于掩盖照相彩色透明胶片。这对于控制用于光机械复制的透明胶片的密度范围特别有用。

锐化蒙版的简化原理

参考知乎链接