【论文笔记】(DGCN-HN) Deep Graph Convolutional Networks with Hybrid Normalization for Accurate and …

本文发表在KDD 2021上

在LR-GCCF和LightGCN的基础上，同时结合了 left normalization (给不同的邻居分配相等的归一化，PinSAGE)和 symmetric normalization （degree大的邻居分配小权重，LightCGN）

1. Intro

1.1 层数不够

基于GCN的模型在浅层就达到了最佳性能，这就没有使用到高阶信号

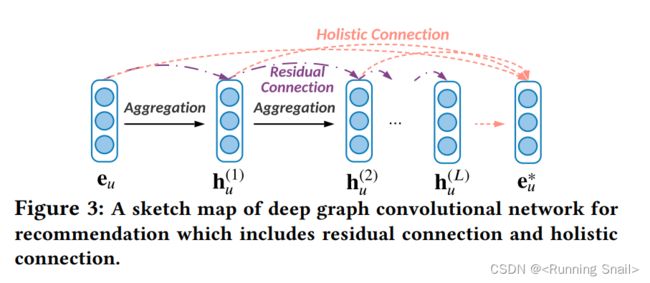
加入残差连接和整体连接（holistic connection）。

提出的模型能将图卷积加深至8层。

1.2 使用固定的归一化规则

基于GCN的模型，对于聚合邻域信息使用的是一样的归一化规则，使得邻居的重要性变得同等重要

• left normalization（左归一化），给不同的邻居分配相同的归一化
• symmetric normalization（对称归一化），给流行的邻居分配较小的权重，给不流行的邻居分配较大的权重

1. 使用固定的归一化规则会导致次优的结果，文章从准确度和多样性的角度探索了左归一化和对称归一化的效果。
2. 节点之间有内在的差异，需要使用不同的归一化来聚合邻域信息。提出了一个新的模型：混合归一化的深度卷积网络(DGCN-HN)。
   混合归一化层和简化的注意力网络，通过自适应地融合来自不同归一化规则的信息，更灵活地建模邻居重要性

• 浅层GCN不能利用高阶信号，给喜欢电子产品的$u_2$推荐无人机就需要高阶信号。
• 给所有节点使用 left normalization ，流行度很高的IPhone就会严重影响$u_1$的兴趣，$u_1$买IPhone只是刚需，兴趣并不在电子产品，因为$u_1$经常购买纸质文具。
• 给所有节点使用 symmetric normalization，流行度很高的IPhone就无法提供”电子产品“这一兴趣，$u_2$和$u_3$的兴趣就难以被刻画出来。

2. METHOD

包括三个主要组成：

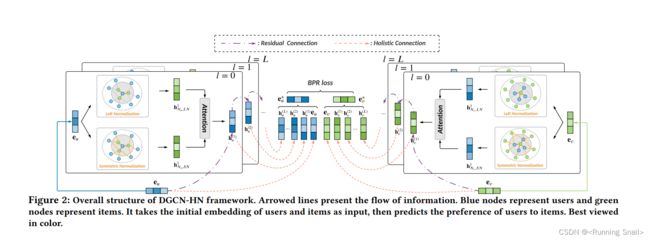
• 设计了带有残差和整体连接的深度图卷积网络推荐
• 引入混合归一化层对邻居重要性进行灵活建模，将左归一化和对称归一化相结合
• 提出一种简化的注意力网络，自适应融合不同归一化方法表示信息

2.1 Deep Graph Convolutional Network for Recommendation

每层的线性聚合可以表示为残差连接，公式如下：
$$h_u^{(l+1)}=\sum _{v\in N_u}{\tilde{A}}_{uv}{h}_v^{(l)}+h_u^{(l)},h_u^{(0)}=e_u$$

$$h_v^{(l+1)}=\sum _{u\in N_v}{\tilde{A}}_{vu}{h}_u^{(l)}+h_v^l,h_v^{(0)}=e_v$$

在经过L层的聚合后，使用整体连接把所有层的表示进行整合，模型使用基于元素的平均聚合作为最后一层的融合策略。公式如下：
$$e_u^{\ast }=\frac{1}{L+1}\sum _{i=0}^L{h}_u^{(i)}$$
$$e_v^{\ast }=\frac{1}{L+1}\sum _{j=0}^L{h}_v^{(j)}$$

（这一部分的作用有待商讨，见最后实验）

2.2 Hybrid Normalization for Flexible Modeling of Neighbor Importance

以user节点为例，对称归一化的公式如下：

$${\mathbf{h}}_u^{(l+1)}=\sum _{v\in N_u}\frac{1}{\sqrt{\left|N_u\right|}\sqrt{\left|N_v\right|}}{\mathbf{h}}_v^{(l)}+{\mathbf{h}}_u^{(l)}$$
左归一化的公式如下：
$$h_u^{(l+1)}=\sum _{v\in N_u}\frac{1}{\left|N_u\right|}{h}_v^{(l)}+h_u^{(l)}$$

2.3 Simplified Attention Network for Adaptive Combination

为结合两种归一化的优点，最简单就是平均加和，复杂一点，加权平均，加上Attention

${\mathbf{h}}_{N_u,LN}^{(l)}$和 ${\mathbf{h}}_{N_u,SN}^{(l)}$，表示左归一化和对称归一化，以用户节点为例，节点更新公式如下：
$$h_{N_u,LN}^{(l+1)}=\sum _{v\in N_u}\frac{1}{\left|N_u\right|}{h}_v^{(l)}$$

$${\mathbf{h}}_{N_u,SN}^{(l+1)}=\sum _{v\in N_u}\frac{1}{\sqrt{\left|N_u\right|}\sqrt{\left|N_v\right|}}{\mathbf{h}}_v^{(l)}$$

$${\mathbf{h}}_u^{(l+1)}={\mathbf{h}}_u^{(l)}+{\alpha }_{u,LN}^{(l+1)}{\mathbf{h}}_{N_u,LN}^{(l+1)}+{\alpha }_{u,SN}^{(l+1)}{\mathbf{h}}_{N_u,SN}^{(l+1)}$$

其中，${\alpha }_{u,\ast }^l$表示不同层的归一化注意力分数。

计算注意分数时，考虑了两个方面：

• 邻居的自信息
• 中心表示和邻居表示之间的相似性

注意力网络的公式如下：
$$z_{u,\ast }^{(l+1)}={\mathbf{W}}_1^{(l)}\sigma \left({\mathbf{W}}_2^{(l)}\left({\mathbf{h}}_{N_{u,\ast }}^{(l+1)}+{\mathbf{h}}_{N_u,\ast }^{(l+1)}\odot {\mathbf{h}}_u^{(l)}\right)\right)$$

其中，$z_{u,\ast }^{(l+1)}$是归一化之前的注意力评分，$W_1^{(l)}\in {\mathbb{R}}^{1\times d^t},W_2^{(l)}\in {\mathbb{R}}^{d^t\times d^l}$是特征变换矩阵，$\sigma$是激活函数，$d^t$是注意力网络的隐藏层的维数。$\odot$表示哈达玛积，对应位置的元素相乘。

结果实验上训不起来无法收敛，换了一个简单的，去除了特征变换矩阵和激活函数，使用平均聚合，得到简化的注意力网络如下：
$$z_{u,\ast }^{(l+1)}=\mathrm{ave}\left({\mathbf{h}}_{N_u,\ast }^{(l+1)}+{\mathbf{h}}_{N_u,\ast }^{(l+1)}\odot {\mathbf{h}}_u^{(l)}\right)$$
之后使用Softmax函数得到$\alpha$，公式如下：
$${\alpha }_{u,\ast }^{(l)}=\frac{exp(z_{u,\ast }^{(l)})}{{\sum }_{k\in LN,SN}exp(z_{u,k}^{(l)})}$$
损失函数为BPR loss

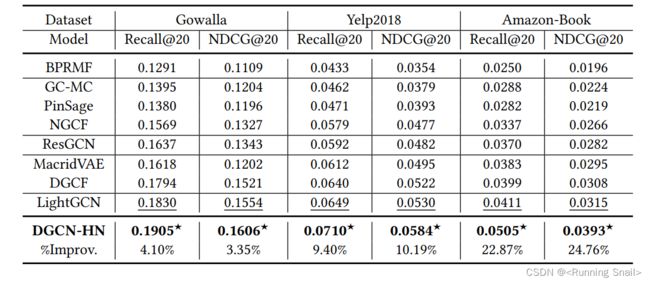
3. EXPERIMENTS

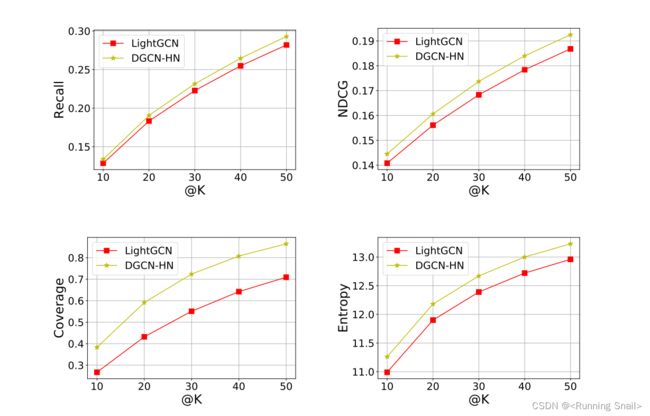
• 覆盖率（Coverage）最简单的定义是，推荐系统能够推荐出来的物品占总物品的比例。覆盖率越高表明模型能够针对更多的item产生推荐，从而促进长尾效应的挖掘。
  Coverage@k的上界为1越大越好，推荐给用户的项目越多。
• Entropy@K侧重于不同项目的分配推荐。它根据不同轮次的推荐次数计算熵值。熵值越大，说明多样性越好，说明的异质性推荐项目高。

文章还考虑到了推荐结果的多样性，结果如下图：

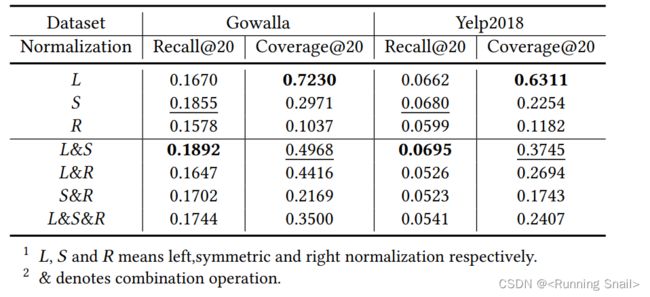
不同归一化方案在GCN上的效果：

可以看出

• 使用单一归一化时，左归一化获得最佳分集，对称归一化获得最佳精度，右归一化在各方面表现最差
• 混合归一化中，左归一化和对称归一化的结合获得了最好的精度和多样性

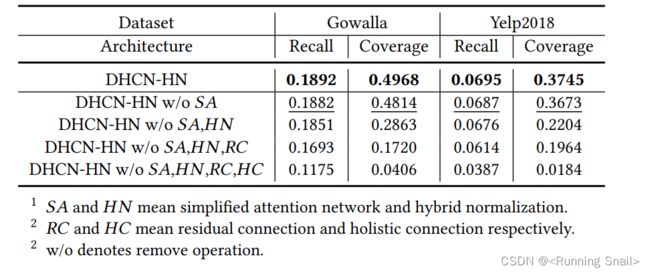
消融实验：

• 引入的简化注意力网络提高了准确率，增加了多样性
• 混合归一化在两个数据集上有显著的性能改善，特别是对于Coverage的提升

总结：

1. 文章从准确度和多样性的角度探索了左归一化和对称归一化的效果。作者能提出这种想法，是跳出了GCN模型本身，考虑了推荐与其他任务的差异，与实际相联系。

2. 按照作者的实验，即使只加入残差，效果也有较大的提升，但这与我们之前自己的实验是相反的。