数据结构与算法学习⑧(自平衡二叉搜索树旋转和实现 手撕红黑树插入与删除)
数据结构与算法学习⑧
- 数据结构与算法学习⑧
-
- 1、AVL树
-
- 1.1、定义及特点
- 1.2、四种失衡及旋转
- 1.3、AVL的实现
- 2、红黑树
-
- 2.1红黑树的定义及特点
- 2.2红黑树的实现-添加
-
- 实现之前讲讲旋转
- 开始实现
- 2.3红黑树的实现-删除
-
- 删除的所有情况
-
- 删除度为1的黑色节点
- 删除度为0的黑色节点
- 删除总结
- 删除代码
数据结构与算法学习⑧
1、AVL树
在前面的课程中,我们学习了二叉搜索树(BST),它的插入、删除、查找操作时间复杂度在最好情况下才是 O(log n),不过在二叉查找树频繁的动态更新过程中,会逐渐退化直至最坏的情况变为链表,
时间复杂度退化为O(n),所以我们要解决这种复杂度退化的问题就要找到一种平衡二叉树,平衡二叉查找树中“平衡”的意思,其实就是让整棵树左右看起来比较“对称”、比较“平衡”,不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些,相应的插入、删除、查找等操作的效率高一些。
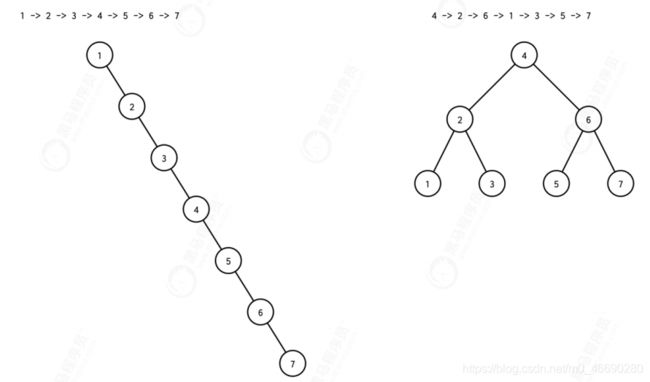
在根据输入的数据构建 BST 树时,特别依赖输入数据是否有序,如果输入数据相对有序那产生的树的结构会非常的不平衡,那查询等相关操作的效率会受到影响。
平衡二叉查找树:简称平衡二叉树,发明平衡二叉查找树这类数据结构的初衷是,解决普通二叉查找树在频繁的插入、删除等动态更新的情况下,出现时间复杂度退化的问题。
也就是说这类二叉搜索树在插入,删除操作后,如果树失去了平衡,它能通过一些操作自平衡。常见的有 AVL 树,红黑树等。
1.1、定义及特点
AVL树是最早发明的自平衡二叉搜索树之一,由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962年提出的高度平衡的二叉树,根据科学家的英文名也称为 AVL 树。它的定义如下:
1:它是一棵 BST 树
2:它的每个节点左右子树高度之差(简称平衡因子/Balance Factor)绝对值不超过1
3:可以是空树,如果不是空树,任何一个结点的左子树与右子树都是平衡
二叉树的高度有两种定义:
- 从根节点到最深节点的最长路径的节点数。
- 从根到最深节点的最长路径的边数。
如果采用第一种定义:空树的高度为0,叶子节点的高度为1
如果采用第二种定义:空树的高度为-1,叶子节点的高度为0
两种均可,为了便于理解我们取第一种定义(因为只需要数节点数即可)
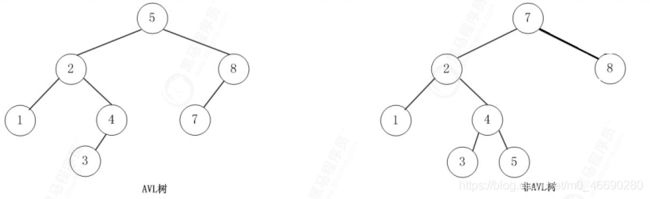
图二中:7的左子树是一棵avl树,但是整体并非avl树
AVL树具备以下的一些特点:
1、对于给定结点数为n的AVL树,最大高度为O(log2 n),也就说,从n个数中,查找一个特定值的时间复杂度是O(log n)。因此,AVL 是一种特别适合进行查找操作的树,,此外在AVL树中插入,删除操作的时间复杂度均为O(n)
2、在平衡二叉树中,当我们插入新元素或删除某元素时,为了保证二叉搜索树的特性,很容易导致某些结点失衡,即该结点的平衡因子大于1,而平衡二叉树的平衡二字体现了它可以自动恢复平衡,这个自动平衡的过程是通过旋转来完成的。
1.2、四种失衡及旋转
在平衡二叉树的插入和删除操作中,某些节点会失去平衡,我们先来看插入的情况,如果A是一颗平衡二叉树,如果新插入一个元素,会有两个结果
- 平衡没有被打破,不用调整
- 平衡被打破,需要调整
对于任意一次插入所造成的不平衡,都可以简化为下列4中情况
情况1-RR:插入节点在失衡节点右子树的右边,我们要对失衡节点进行左旋
图解如下:失衡节点的平衡因子为 -2
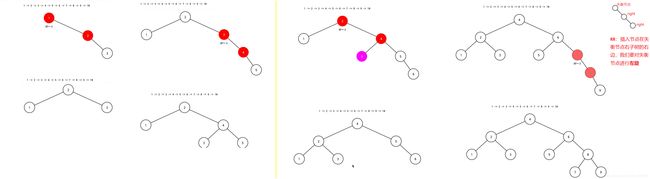
情况2-LL:插入节点在失衡节点左子树的左边,我们需要对失衡节点进行右旋

与此同时,我们发现,左旋和右旋操作其实是成镜像关系的。
情况3-LR:插入节点在失衡节点左子树的右边,先对失衡节点的左子树左旋(左子树为RR情况),再对失衡节点右旋(失衡节点为LL情况)

情况4-RL:插入节点在失衡节点右子树的左边,先对失衡节点右子树右旋(右子树为LL情况),再对失衡节点左旋(失衡节点为RR情况)

总结:
RR左旋失衡结点
LL右旋失衡节点
LR左旋失衡节点的左子树,然后再对失衡节点右旋
RL右旋失衡结点的右子树,然后再对失衡节点左旋
旋转有点像跷跷板,左旋,左边下去了。右旋,右边下去了
1.3、AVL的实现
1、创建AVL树,定义树的节点 AvlNode
public class AvlTree {
AvlNode root;
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("该树的前序遍历结果为:");
preOrder(root,sb);
sb.append("该树的中序遍历结果为:");
inOrder(root,sb);
sb.append("该树的后序遍历结构为:");
postOrder(root,sb);
return sb.toString();
}
private void inOrder(AvlNode node, StringBuilder sb) {
if (node == null) {
return;
}
inOrder(node.left,sb);
sb.append(node.key).append("->");
inOrder(node.right,sb);
}
private void preOrder(AvlNode node, StringBuilder sb) {
if (node == null) {
return;
}
sb.append(node.key).append("->");
preOrder(node.left,sb); preOrder(node.right,sb);
}
private void postOrder(AvlNode node, StringBuilder sb) {
if (node == null) {
return;
}
postOrder(node.left,sb);
postOrder(node.right,sb);
sb.append(node.key).append("->");
}
public static class AvlNode{
int key;
AvlNode left;
AvlNode right;
/*** 我们取第一种高度定义:从根节点到最深节点的最长路径的节点数
* * 故:空树高度记为0,叶子节点高度记为1 */
int height =1; public AvlNode(int key) {
this.key = key; }
}
}
2、定义一个方法用以获取节点的高度
/** 获取节点的高度
* 这里高度的定义是:从根节点到最深节点的最长路径的节点数。
* @param node * @return */
public int getHeight(AvlNode node){
return node == null ? 0 : node.height;// 空树的高度为0
}
3、编写一个函数针对 RR 情况进行旋转 public AvlNode RRrotate(AvlNode unbalance) {
/** * RR旋转:对失衡节点进行左旋 *
* 20 30
* / \ / \
* 10 30 20 40
* / \ --RR旋转- / \ \
* 25 40 10 25 50
* \
* 50
* @param unbalance 失衡节点
* @return 调整后的根节点 */
public AvlNode RRrotate(AvlNode unbalance) {// 20为失衡点
AvlNode root = unbalance.right;//失衡点的右子树的根结点30作为新的根结点
unbalance.right = root.left;//将新的根结点的左子树25成为失衡点20的右子树
root.left = unbalance; // 将失衡点20作为新的根结点的左子树
/**
* 重新设置失衡点20和新节点30的高度 其他节点的高度不变
* 节点高度如何确定?
* 节点的高度= Math.max(左子树的高度,右子树的高度) +1 */
unbalance.height = Math.max(getHeight(unbalance.left),getHeight(unbalance.right)) +1;
root.height = Math.max(getHeight(root.left),getHeight(root.right)) +1;
return root;// 新的根节点取代原失衡点的位置 }
4、编写一个函数针对 LL 情况进行旋转: public AvlNode LLrotate(AvlNode unbalance) {
/** * LL旋转:对失衡节点进行右旋 *
* 30 20
* / \ / \
* 20 40 10 30
* / \ --LL旋转- / / \
*10 25 5 25 40
5、编写两个函数分别针对 LR,RL 两种情况进行旋转
6、编写插入操作,插入操作要注意几点
AVL 树也是一棵 BST 树,插入要符合 BST 树的特征
插入操作涉及到从根节点开始依次进行比较,直到插入。插入完成后要从原路回溯查找失衡节
点,并且进行旋转调整,故相对较好的实现方式是基于递归来完成。
* / * 5 * @param unbalance 失衡节点 * @return 调整后的根节点 */
public AvlNode LLrotate(AvlNode unbalance) { // 30为失衡点
AvlNode root = unbalance.left;//失衡点的左子树的根结点20作为新的根结点
unbalance.left = root.right;//将新的根结点的右子树25成为失衡点30的左子树
root.right = unbalance;// 将失衡点30作为新的根结点的右子树
// 重新设置失衡点30和新节点20的高度
unbalance.height = Math.max(getHeight(unbalance.left),getHeight(unbalance.right)) +1;
root.height = Math.max(getHeight(root.left),getHeight(root.right)) +1;
return root;
}
5、编写两个函数分别针对 LR,RL 两种情况进行旋转
/** *
* LR旋转:先对失衡节点的左子树按RR情况处理,再对失衡节点按LL处理
* * @param unbalance
* * @return */
public AvlNode LRrotate(AvlNode unbalance) {
unbalance.left = RRrotate(unbalance.left); // 先将失衡点的左子树进行RR旋转
return LLrotate(unbalance);// 再将失衡点进行LL平衡旋转并返回新节点代替原失衡点
}
/** * RL旋转:先对失衡节点的右子树按LL情况处理,再对失衡节点按RR情况处理
* @param unbalance
* @return */
public AvlNode RLrotate(AvlNode unbalance) {
unbalance.right = LLrotate(unbalance.right);// 先将失衡点的右子树进行LL平衡 旋转
return RRrotate(unbalance);// 再将失衡点进行RR平衡旋转并返回新节点代替原失衡点
}
6、编写插入操作,插入操作要注意几点
- AVL 树也是一棵 BST 树,插入要符合 BST 树的特征
- 插入操作涉及到从根节点开始依次进行比较,直到插入。插入完成后要从原路回溯查找失衡节
点,并且进行旋转调整,故相对较好的实现方式是基于递归来完成。
public void insert(int key) {
this.root = insert(this.root, key);
}
/**
* 针对一棵二叉搜索树,通过递归的方式去插入
* 同时在回溯的过程中找到失衡节点,判断属于RR,LL,LR,RL中的哪种情况,进行旋转调整,
* 最后插入路线上的每个节点需要重新调整高度
* 7、编写测试代码进行测试:
**/
public AvlNode insert(AvlNode tree, int key) {
//terminal
if (tree == null) {
tree = new AvlNode(key);
return tree;
}
//current logic
/**
* 判断 key是插入到tree的左子树还是右子树
* 回溯的过程中判断该节点是否失衡
* 如果失衡判断属于哪种情况,根据情况进行调整 */
if (key > tree.key) { //插入到右子树
//drill down 插入到右子树
tree.right = insert(tree.right, key);
//判断当前节点tree是否失衡
if (Math.abs(getHeight(tree.left) - getHeight(tree.right)) > 1) {
//判断属于RR 还是RL
if (key > tree.right.key) {
//RR情况
tree = RRrotate(tree);
} else {
//RL情况
tree = RLrotate(tree);
}
}
} else if (key < tree.key) { //插入到左子树
//drill down 插入到左子树
tree.left = insert(tree.left, key);
//判断当前节点tree是否失衡
if (Math.abs(getHeight(tree.left) - getHeight(tree.right)) > 1) {
//判断属于LL,还是LR
if (key < tree.left.key) {
//LL情况
tree = LLrotate(tree);
} else {
//LR情况
tree = LRrotate(tree);
}
}
} else {
//根据情况,不做操作或者更新该节点
}
tree.height = Math.max(getHeight(tree.left),getHeight(tree.right)) +1;
return tree;
}
7、编写测试代码进行测试
比对RR,RL,LR,RL的四张图片测试理解。
public static void main(String[] args) {
//testRR();
// testLL();
// testLR();
// testRL();
}
//测试RR情况
public static void testRR(){
AvlTree avlTree = new AvlTree();
avlTree.insert(1);
avlTree.insert(2);
avlTree.insert(3);
System.out.println(avlTree);
avlTree.insert(4);
avlTree.insert(5);
System.out.println(avlTree);
avlTree.insert(6);
System.out.println(avlTree);
avlTree.insert(7);
avlTree.insert(8);
avlTree.insert(9);
System.out.println(avlTree);
avlTree.insert(10);
}
public static void testLL(){
AvlTree avlTree = new AvlTree();
avlTree.insert(10);
avlTree.insert(9);
avlTree.insert(8);
System.out.println(avlTree);
avlTree.insert(7);
avlTree.insert(6);
System.out.println(avlTree);
avlTree.insert(5);
System.out.println(avlTree);
avlTree.insert(4);
avlTree.insert(3);
avlTree.insert(2);
avlTree.insert(1);
System.out.println(avlTree);
}
public static void testLR(){
AvlTree avlTree = new AvlTree();
avlTree.insert(10);
avlTree.insert(7);
avlTree.insert(9);
System.out.println(avlTree);
avlTree.insert(2);
avlTree.insert(5);
avlTree.insert(6);
System.out.println(avlTree);
avlTree.insert(3);
avlTree.insert(1);
avlTree.insert(4);
System.out.println(avlTree);
}
public static void testRL(){
AvlTree avlTree = new AvlTree();
avlTree.insert(1);
avlTree.insert(4);
avlTree.insert(2);
System.out.println(avlTree);
avlTree.insert(9);
avlTree.insert(6);
System.out.println(avlTree);
avlTree.insert(5);
System.out.println(avlTree);
avlTree.insert(8);
avlTree.insert(10);
avlTree.insert(7);
System.out.println(avlTree);
}
9、面试实战题目
1382. 将二叉搜索树变平衡
进阶:对于AVL树的查询操作和删除操作应该如何来完成呢?
1、对于查询,AVL树也是一棵BST树,所以查询操作跟BST的查询操作一样,比较简单,复杂
度O(log n)
2、对于删除,删除情况跟BST树一样,只不过删除之后也需要查找失衡节点并进行自平衡操
作。
2、红黑树
2.1红黑树的定义及特点
在前面的章节中我们讲到了AVL树这样一个平衡二叉查找树数据结构,它能够做到插入,删除,查询的时间复杂度为O(log n),AVL树是一种非常严格的平衡二叉树并且它也是自平衡的,AVL树有很多好处但也有弊端,AVL 树为了维持这种高度的平衡,就要付出更多的代价。每次插入、删除都要做调整,就比较复杂、耗时。所以,对于有频繁的插入、删除操作的数据集合,使用 AVL 树的代价就有点高了。
其实平衡二叉查找树有很多,接下来我们学习一种数据结构叫红黑树,红黑树是一种比较难的数据结构,但是又由于红黑树是一种性能非常稳定的二叉查找树,所以,在工程中,但凡是用到动态插入、删除、查找数据的场景,都可以用到它。红黑树也是为了解决普通二叉查找树在数据更新的过程中,复杂度退化的问题而产生的。
红黑树(Red Black Tree):也是一种自平衡的二叉搜索树,之前叫做平衡二叉B树(SymmetricBinary B-Tree)。

首先,红黑树也是一棵二叉搜索树 BST ,因此它也满足 BST 树的所有特征。除此之外,它必须满足
以下5条性质:
- 性质1:节点具备颜色,要么是红色(RED),要么是黑色(BLACK)。
- 性质2:根节点是黑色(BLACK)。
- 性质3:叶子节点都是黑色(BLACK)的空节点,也不存数据。
注意:
1、红黑树中的叶子节点并非我们之前所讲的叶子节点,红黑树中的叶子节点是假想出来的,是为了配合它的一些性质而产生的(在java中就是为null的空节点)。
2、红黑树这样定义叶子节点,会让原来度为0及度为1的节点都变成度为2的节点。另外:在后续讲解过程中,我们将叶子节点省略,但要认识到它的存在! - 性质4:红黑树中,红色(RED)节点的子节点都是黑色(BLACK)
注意:由红黑树的这一性质可推导出两个结论
1、红色节点的父节点都是黑色
2、从根节点到叶子节点的所有路径上不能有2个连续的红色(RED)节点 - 性质5:从任一节点到叶子节点的所有路径都包含相同数目的黑色(BLACK)节点
总之:在这些规则的约束下,红黑树能够保证平衡。
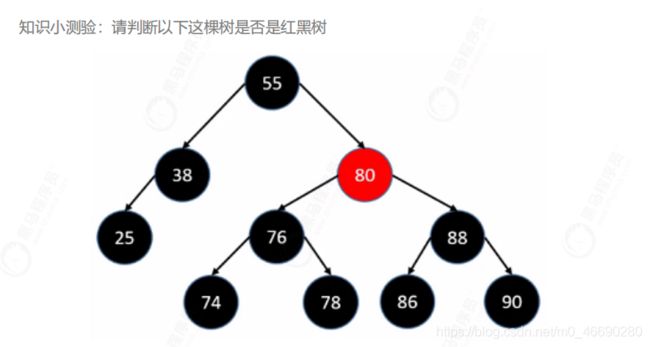
这不是一颗红黑树,性质3的关系,每个节点都伸出两个叶子节点null,38这个节点右拉出个叶子节点(假想),从叶子节点出发,只有3个黑色节点,而其他的都是4个节点,所以违反了性质5
2.2红黑树的实现-添加
实现之前讲讲旋转
新添加的节点应该是什么颜色?

第一类:有4种情况
父节点为黑色:此时仍然满足红黑树的所有性质,无需处理
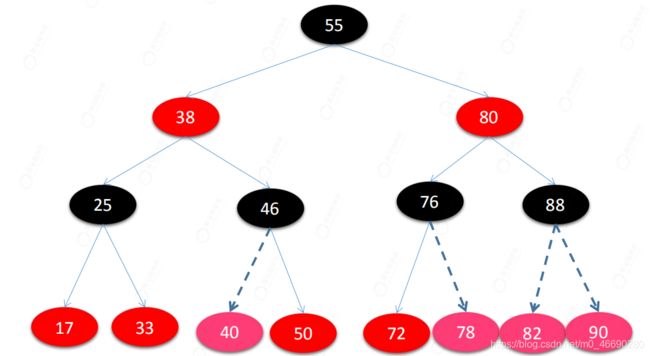
第二类:有8种情况
父节点为红色 , 违反了性质4,出现Double Red,我们需要针对这8种情况进行调整

判断条件:叔父节点不是红色(这句是重点,叔父不是红色说明右边或者左边缺失了,也就是不平衡得情况,需要旋转来维持平衡)
修复性质4-RR/LL
RR
父节点为红色
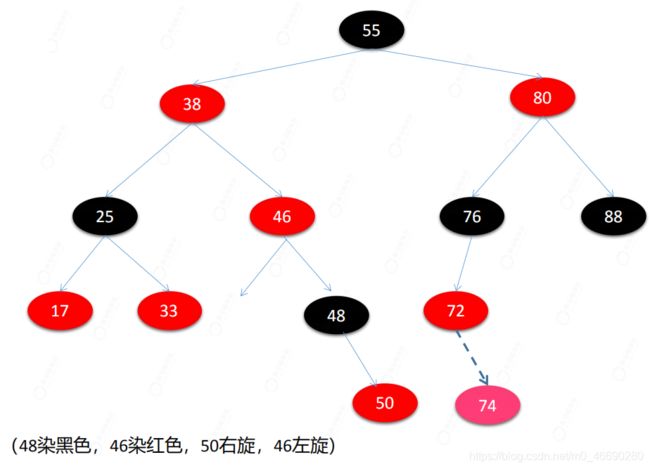
38->46->50->52
因为52插入导致违反了性质4,插入默认为红色,需要的操作是:
父节点染黑,祖父节点染红,也就是说50染黑,46染红,46左旋操作,
LL
80->76->72->60
因为60插入导致违反了性质4,
父节点染黑,祖父节点染红,72黑76红,76右旋操作
1、染色:自己染成黑色, 祖父节点染成红色
判断条件:叔父节点不是红色(这句是重点,叔父不是红色说明右边或者左边缺失了,也就是不平衡得情况,需要旋转来维持平衡)
添加-修复性质4-LR/RL
一样得染色操作
自己变黑,祖父变黑
RL
只是旋转这一块,先右父节点,再左旋祖父节点
LR:父节点左旋,祖父右旋
RL:父节点右旋,祖父左旋
修复性质4-LL/RR/LR/RL
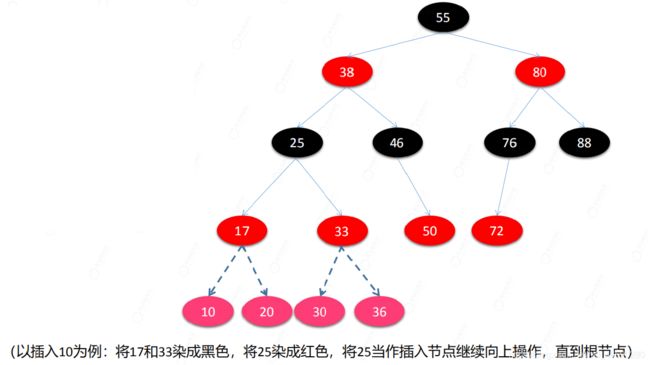
判断条件:叔父节点是红色(叔父是红色节点说明是平衡的,只需要染色即可,递归染色)
父节点和叔父节点染成黑色,祖父节点染成红色,这样就红黑红了,递归,最终到根节点,根节点是终止条件染成黑色

注意:
1.父节点为红色,祖父节点是黑色,这个黑色是假象的,脑补出来的null,也就是性质3中的(性质3:叶子节点都是黑色(BLACK)的空节点,也不存数据),这种情况需要RR,LL,RL,LR旋转的,其他只需要染色或者不操作即可
2.这里有别于AVL(自平衡树),自平衡拿失衡节点做操作的,而这个红黑树是根据插入节点操作的。所以需要存父节点
开始实现
先构造一些实用的方法
public class RBTree {
private static final boolean RED = false;
private static final boolean BLACK = true;
Node root;//
//给节点node染色并返回该节点
private Node color(Node node, boolean color) {
if (node == null) {
return node;
}
node.color = color;
return node;
}
//将节点染成红色
public Node red(Node node) {
return color(node, RED);
}
//将节点染成黑色
public Node black(Node node) {
return color(node, BLACK);
}
//返回节点的颜色
public boolean colorOf(Node node) {
return node == null ? BLACK : node.color;
}
//判断是否是黑色
public boolean isBlack(Node node) {
return colorOf(node) == BLACK;
}
//判断是否是红色
public boolean isRed(Node node) {
return colorOf(node) == RED;
}
@Override
public Object root() {
return root;
}
@Override
public Object left(Object node) {
return ((Node) node).left;
}
@Override
public Object right(Object node) {
return ((Node) node).right;
}
@Override
public Object string(Object node) {
return node;
}
public static class Node {
int key;
boolean color = RED;//代表节点的颜色 RED=false BLACK=true
Node left;
Node right;
Node parent;
public Node(int key, Node parent) {
this.key = key;
this.parent = parent;
}
//判断当前节点是否是最后一层的叶子
public boolean isLeaf() {
return left == null && right == null;
}
//判断是否有两个节点
public boolean hasTwoChildren() {
return left != null && right != null;
}
//判断当前节点是否是其父节点的左子节点
public boolean isLeftChild() {
return parent != null && this == parent.left;
}
//判断当前节点是否是其父节点的右子节点
public boolean isRightChild() {
return parent != null && this == parent.right;
}
//获取当前节点的兄弟节点
public Node sibling() {
if (isLeftChild()) {
return parent.right;
}
if (isRightChild()) {
return parent.left;
}
return null;
}
@Override
public String toString() {
String str = "";
if (color == RED) {
str = "R_";
}
return str + key;
}
}
添加
public void add(int key) {
//判断传入元素
//判断root是否为空元素
if (root == null) {
root = new Node(key, null);
afterAdd(root);
return;
}
//找到新节点应插入到哪个位置
Node parent = null;
Node curr = root;
while (curr != null) {
parent = curr;
//插入的元素大了,右
if (key > curr.key) {
curr = curr.right;
} else if (key < curr.key) {
curr = curr.left;
}
}
//完毕之后跑到要添加的节点位置了
Node newNode = new Node(key, parent);
//父节点指针先指向子节点
if (key > parent.key) {
parent.right = newNode;
} else if (key < parent.key) {
parent.left = newNode;
}
afterAdd(newNode);
}
public void afterAdd(Node node) {
Node parent = node.parent;
//判断父节点是否为空,空说明是根节点,染成黑色
if (parent == null) {
black(node);
return;
}
//如果父节点是黑色,那就不用操作了
if (isBlack(parent)) {
return;
}
//如果父节点是红色的话又要分两种情况了(叔父是红色和叔父是黑色)
// 叔父是黑色的话说明不平衡需要旋转,叔父是红色只需要递归染色即可
//拿到叔父节点和祖父节点
Node uncle = parent.sibling();
//祖父节点,后续几个情况都需要祖父节点变成红色,那就先变色吧
Node grand = red(parent.parent);
//如果叔父节点是红色的话,平衡递归染色
if (isRed(uncle)) {
black(uncle);
black(parent);
//染成黑色,递归
afterAdd(grand);
return;
}
//接下来就是LL RR LR RL的情况
//LL RR 父染成黑色,祖父红色,旋转祖父节点
//LR RL自己黑,祖父红
//LR:父节点左旋,祖父右旋 RL:父节点右旋,祖父左旋
if (parent.isLeftChild()) {
if (node.isLeftChild()) {
//左左
black(parent);
// red(grand);
LLroate(grand);
} else {
//LR
black(node);
LRroate(grand);
}
} else {
if (node.isRightChild()) {
//右右
black(parent);
RRroate(grand);
} else {
//RL
black(node);
RLroate(grand);
}
}
}
重点讲一下RR的插入旋转过程
建议截图代码,然后跟着图过,非常有帮助。
private Node RRroate(Node node) {
//RR左旋的操作
Node newParent = node.right;
//newParent的左节点指向node的右节点
node.right = newParent.left;
if (newParent.left != null) {
//newParent的左子树认爸爸,指针相互指对方
newParent.left.parent = node;
}
//node接到newParent上,并且把node的parent让newParent去接,
newParent.left = node;
newParent.parent = node.parent;
//头去判断是放左还是放右
if (node.isLeftChild()) {
node.parent.left = newParent;
} else if (node.isRightChild()) {
node.parent.right = newParent;
} else {
root = newParent;
}
node.parent = newParent;
return newParent;
}
LL情况类似不画图了,建议拿个插入之前的树想过程
private Node LLroate(Node node) {
Node newParent = node.left;
node.left = newParent.right;
if (newParent.right != null) {
newParent.right.parent = node;
}
newParent.right = node;
newParent.parent = node.parent;
if (node.isLeftChild()) {
node.parent.left = newParent;
} else if (node.isRightChild()) {
node.parent.right = newParent;
} else {
root = newParent;
}
node.parent = newParent;
return newParent;
}
LR RL拿子节点转,然后自己转即可
private Node LRroate(Node node) {
RRroate(node.left);
return LLroate(node);
}
private Node RLroate(Node node) {
LLroate(node.right);
return RRroate(node);
}
2.3红黑树的实现-删除
首先,红黑树也是一棵二叉搜索树,对于二叉搜索树的删除,总共可以分为3中情况:
1、删除度为0的节点:直接删除
2、删除度为1的节点:父节点指向其子节点
3、删除度为2的节点:用前驱节点或后继节点替换删除节点,真正被删除的是用以替换的前驱或者后继节点,即回到了前两种情况。
前驱:左子树最大值
后继:右子树最小值

结论:真正被删除的是那些度为0和度为1的节点
删除的所有情况
通过对 BST 树删除情况的分析,红黑树的删除总共有如下几种情况:
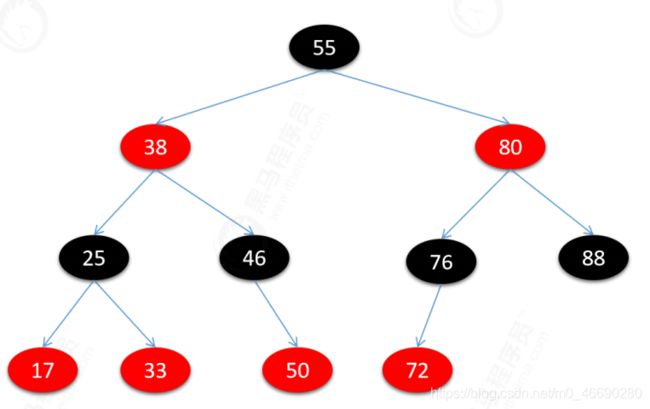
删除的节点是红色节点
直接删除
删除的节点是黑色节点
1.拥有一个黑色子节点
2.最后一层黑色叶子节点(这里不是指想象出来的null)
结论:需要针对删除黑色节点的两种情况进行调整,如果只剩根节点直接删除即可
删除度为1的黑色节点
删除度为0的黑色节点
1.如果被删除节点度为0,且是根节点,则直接删除即可,无需做任何调整。
度为0的非根节点
这个时候需要看兄弟节点了
前提
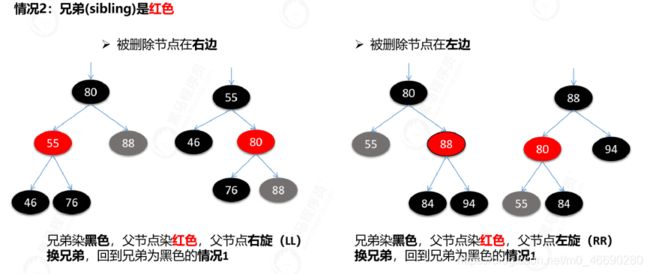
兄弟节点是黑色,并且有红色子节点
被删除节点在左边:父节点RR/RL旋转,旋转后根节点继承父节点颜色,且根节点左右子节点染黑色

注:(二)72的值应改为82
被删除节点在右边:父节点LL/LR旋转,旋转后根节点继承父节点颜色,且根节点左右子节点染黑色
(三)的情况可以看成RL或者RR,建议看成RR,少一次旋转

前提
黑兄弟无红色子节点

没的旋转了,只能染色,父节点是红色的话,会违背性质5,所以向上染色;
父节点是黑色的情况,兄弟染红,父染黑,递归处理.
前提
兄弟节点是红色
删除总结
删除代码
public void remove(int key) {
remove(node(key));
}
private Node node(int key) {
//先找到要删除的节点位置
Node node = root;
while (node != null) {
if (node.key > key) {
node = node.left;
} else if (node.key < key) {
node = node.right;
} else {
return node;
}
}
return null;
}
private void remove(Node node) {
if (node == null) {
return;
}
//如果是度2的节点,也就是有两个子孩子
if (node.hasTwoChildren()) {
//可以采用前驱或者后继节点来代替被删除节点
//这里采用前驱
Node p = node.left;
while (p.right != null) {
p = p.right;
}
//找到后
node.key = p.key;
//接下来真正要删除的是前驱节点了
node = p;
//删除度为1和度为0的节点node
//找到其代替节点
Node replacement = node.left != null ? node.left : node.right;
//父节点认儿子的过程
if (node.parent == null) {
root = replacement;
//判断左右节点
} else if (node.isLeftChild()) {
node.parent.left = replacement;
} else if (node.isRightChild()) {
node.parent.right = replacement;
}
afterRemove(node, replacement);
node.parent = null;
node.left = null;
node.right = null;
}
}
private void afterRemove(Node beRemoved, Node replacement) {
//如果删除的是红色节点,无需调整
if (isRed(beRemoved)) {
return;
}
//被删除的是黑色节点
//如果被删除节点有一个红色的代替子节点(度为1),染色
if (isRed(replacement)) {
black(replacement);
return;
}
//要删除的是度为0的黑色叶子节点
Node parent = beRemoved.parent;
if (parent == null) {
return;
}
//黑色的叶子(且是非根节点)
//获取左边还是右边 前面一段判断左还是右,后面一段为了递归 兄弟黑父也为黑的情况
boolean left = parent.left == null || beRemoved.isLeftChild();
//获取兄弟节点 被删除在左边,那就右边
Node sibling = left ? parent.right : parent.left;
//分左右 删除节点在左边
if (left) {
//判断是否是情况2
if (isRed(sibling)) {
//兄弟为红色
black(sibling);
red(parent);
RRroate(parent);
//换兄弟
sibling = parent.right;
}
//情况1的代码,兄弟为黑色
if (isBlack(sibling.left) && isBlack(sibling.right)) {
boolean parentBlack = isBlack(parent);
red(sibling);
black(parent);
if (parentBlack) {
afterRemove(parent, null);
}
} else {
//黑兄弟有红色子节点
Node newParent;
if (isRed(sibling.right)) {
//rr
newParent = RRroate(parent);
} else {
//rl
newParent = RLroate(parent);
}
//旋转后染色
color(newParent, colorOf(parent));
black(newParent.left);
black(newParent.right);
}
} else {
//判断是否是情况2
if (isRed(sibling)) {
//兄弟为红色
black(sibling);
red(parent);
LLroate(parent);
//换兄弟
sibling = parent.left;
}
//情况1的代码 兄弟为黑色
if (isBlack(sibling.left) && isBlack(sibling.right)) {
//黑兄弟无红色子节点
boolean parentBlack = isBlack(parent);
red(sibling);
black(parent);
if (parentBlack) {
afterRemove(parent, null);
}
} else {
//黑兄弟有红色子节点
Node newParent;
if (isRed(sibling.left)) {
// ll
newParent = LLroate(parent);
} else { // lr
newParent = LRroate(parent);
}
//旋转后的根节点继承父节点的颜色
color(newParent, colorOf(parent));
black(newParent.left);
black(newParent.right);
}
}
}
4、可借助链接进行测试
注意:删除的结果不唯一,该网站在删除度为2的节点时,采用的是用其前驱节点替代,同时
删除逻辑中也有一处可采用不同的逻辑。