十三、聚类算法

六、聚类算法实战

一、聚类

聚类是一种无监督的机器学习任务，可以自动将数据划分为类cluster，因此聚类分组不需要提前被告知所划分的组应该是什么样子的。因为我们甚至可能都不知道我们在寻找什么，所以聚类是用于知识发现而不是预测。
聚类原则是一个组内的记录彼此必须非常相似，而与该组之外的记录截然不同，所有聚类做的就是遍历所有的数据然后找到这些相似性。

二、K-Means(均值)

①选择K个初始的簇中心，该点可以是随机的，也可以是人为的
②某一个样本和某一个聚类中心的距离
③计算所属聚类的样本均值


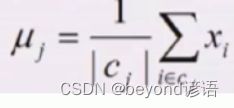
②③循环往复迭代，直到不发生任何变化就停止

三、K-Mediods(中位数)

数组1，2，3，4，100的均值为22，要是通过K-Means求均值的话，离里面大多数的数值还是比较远的
取中位数3的话，更好一些，因为100是个噪声点

四、二分K-Means

两个簇里面的样本数量都很小，两个簇中心很近，两个MSE很小，合并，簇中心离得很远，MSE很大，分开
若发现两个簇中心比较近，就把这两个簇进行合并
若发现某个簇离其他簇都比较远，而且该簇里面点又特别多，那就把这个簇分成两部分

五、K-Means++

选择初始化簇中心稍微远一点
随机选择第一个
算每个样本到第一个样本距离，样本距离可以算成概率
概率化选择

六、Mini Batch K-Means

本质上，以上用的是BGD批量梯度下降，而Mini Batch K-Means使用的是SGD随机梯度下降
从每个簇中不选择全部求均值，而是选择一部分求均值
速度快，数据量大的时候可以选择

七、如何确定K聚类数

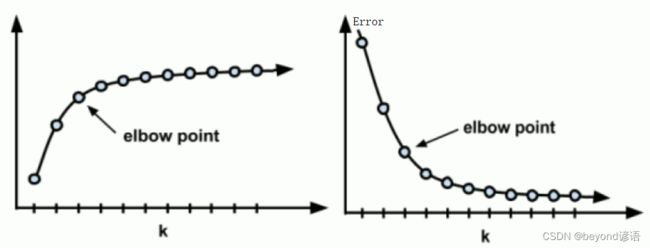
Ⅰ，肘部法

也就是找拐点位置

Ⅱ，K均值损失函数

假定数据点分布符合高斯分布

K个高斯分布混合得到得样本数据分布为
最大似然估计

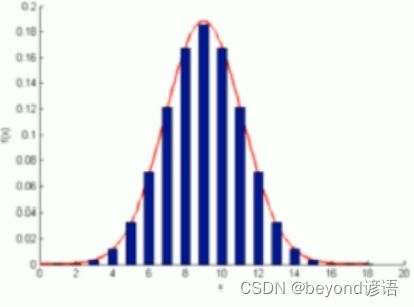
似然函数取最大值
概率密度相乘再各个族似然相乘，找到哪些个μ可以使得取最大值，这个就是K均值得损失函数(从机器学习角度重新看待平方误差)

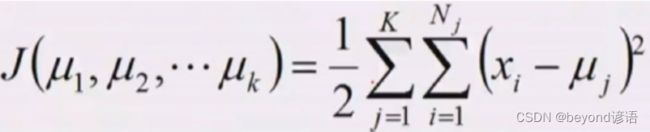
Ⅲ，求偏导

公式化解释K均值
所以K均值假设了高斯混合模型，GMM，并且假设了方差sigma是一样的
K均值是在给定损失函数的情况下，梯度下降的一个应用
高斯混合分布不是线性回归凸函数，有多个极小值
K-Means++或者多算几次
淬火法或遗传算法来计算全局最优解

八，不同的K聚类情况

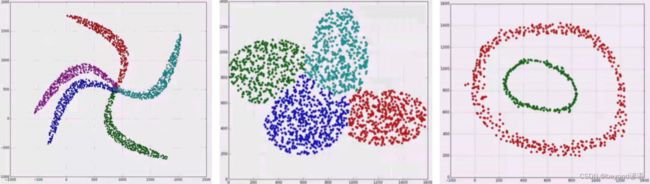
K-Means适用于拿圈来绘制类别，并不适合不规则形状的划分

九、数据分布对K-Means的影响

代码实现

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import KMeans
from sklearn.cluster import MiniBatchKMeans


def expand(a, b):
    d = (b - a) * 0.1
    return a-d, b+d


if __name__ == "__main__":
    N = 400#创建400个样本
    centers = 4#有4个类别
    data, y = ds.make_blobs(N, n_features=2, centers=centers, random_state=2)#创建一些聚类的模拟数据
    data2, y2 = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=(1, 2.5, 0.5, 2), random_state=2)
    data3 = np.vstack((data[y == 0][:], data[y == 1][:50], data[y == 2][:20], data[y == 3][:5]))
    y3 = np.array([0] * 100 + [1] * 50 + [2] * 20 + [3] * 5)

    cls = KMeans(n_clusters=4, init='k-means++')
    y_hat = cls.fit_predict(data)
    y2_hat = cls.fit_predict(data2)
    y3_hat = cls.fit_predict(data3)

    m = np.array(((1, 1), (1, 3)))
    data_r = data.dot(m)
    y_r_hat = cls.fit_predict(data_r)

    matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
    matplotlib.rcParams['axes.unicode_minus'] = False
    cm = matplotlib.colors.ListedColormap(list('rgbm'))

    plt.figure(figsize=(9, 10), facecolor='w')
    plt.subplot(421)
    plt.title(u'原始数据')
    plt.scatter(data[:, 0], data[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
    x1_min, x2_min = np.min(data, axis=0)
    x1_max, x2_max = np.max(data, axis=0)
    x1_min, x1_max = expand(x1_min, x1_max)
    x2_min, x2_max = expand(x2_min, x2_max)
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.grid(True)

    plt.subplot(422)
    plt.title(u'KMeans++聚类')
    plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none')
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.grid(True)

    plt.subplot(423)
    plt.title(u'旋转后数据')
    plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
    x1_min, x2_min = np.min(data_r, axis=0)
    x1_max, x2_max = np.max(data_r, axis=0)
    x1_min, x1_max = expand(x1_min, x1_max)
    x2_min, x2_max = expand(x2_min, x2_max)
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.grid(True)

    plt.subplot(424)
    plt.title(u'旋转后KMeans++聚类')
    plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none')
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.grid(True)

    plt.subplot(425)
    plt.title(u'方差不相等数据')
    plt.scatter(data2[:, 0], data2[:, 1], c=y2, s=30, cmap=cm, edgecolors='none')
    x1_min, x2_min = np.min(data2, axis=0)
    x1_max, x2_max = np.max(data2, axis=0)
    x1_min, x1_max = expand(x1_min, x1_max)
    x2_min, x2_max = expand(x2_min, x2_max)
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.grid(True)

    plt.subplot(426)
    plt.title(u'方差不相等KMeans++聚类')
    plt.scatter(data2[:, 0], data2[:, 1], c=y2_hat, s=30, cmap=cm, edgecolors='none')
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.grid(True)

    plt.subplot(427)
    plt.title(u'数量不相等数据')
    plt.scatter(data3[:, 0], data3[:, 1], s=30, c=y3, cmap=cm, edgecolors='none')
    x1_min, x2_min = np.min(data3, axis=0)
    x1_max, x2_max = np.max(data3, axis=0)
    x1_min, x1_max = expand(x1_min, x1_max)
    x2_min, x2_max = expand(x2_min, x2_max)
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.grid(True)

    plt.subplot(428)
    plt.title(u'数量不相等KMeans++聚类')
    plt.scatter(data3[:, 0], data3[:, 1], c=y3_hat, s=30, cmap=cm, edgecolors='none')
    plt.xlim((x1_min, x1_max))
    plt.ylim((x2_min, x2_max))
    plt.grid(True)

    #plt.tight_layout(2, rect=(0, 0, 1, 0.97))
    plt.tight_layout()
    plt.suptitle(u'数据分布对KMeans聚类的影响', fontsize=18)
    # https://github.com/matplotlib/matplotlib/issues/829
    # plt.subplots_adjust(top=0.92)
    plt.show()
    # plt.savefig('cluster_kmeans')

十、Canopy算法

K-Means聚类都是多次的迭代进行划分，而Canopy仅进行一次迭代出结果
一次迭代很多情况下对机器学习并不是特别的适用
Canopy一次迭代的主要目的是：找到初始的K个中心点！有两个超参数T1和T2

聚类流程：①找初始的中心点 ②进行相对于的隶属关系点的划分

Canopy与K-Means区别：
①Canopy会让周围的点不再可能成为新的中心点，这样使得划分的比较均匀
②K-Means中的类别K需要指定，但Canopy算法中不需要指定K，有多少的类别就看所有点都归结为某类时，停止迭代之后有系统划分为多少类
③Canopy中的点可能会被划分为多个类别中去
④Canopy是一次迭代，一般一次迭代的东西并不是特别好
⑤K-Means难点在于K个中心点的选取，一般人们普遍通过Canopy来选出中心点，然后人为的把中心点给传给K-Means，Canopy常用作先验知识。

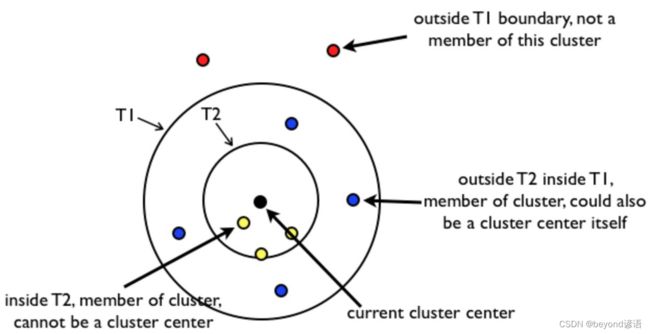
首先随机找到一个中心点，黑色的点
以T2为半径画圈，再这个圈内都的点，也就是黄色的点，和黑色点为同一个类别，这些黄色的点将来不会被随机选择为中心点
以T1为半径，再这个圈内且在T2圈外，也就是蓝色的点，和黑色的点也为同一个类别，这些蓝色的点将来可能会被随机选择为其他簇的中心点
另外在T1全外的红色的点，就和黑色的点不属于同一个类别

例如K=3时，随机选择黑色点为中心点，其中黄色的点和蓝色的点都归结为和黑色点为同一个类别
区分第二个类别时，黄色的不会再动了，随机再从蓝色点和红色点选取一个中心点，以该中心点T1和T2圈内进行划分新的类别，以此类推进行划分新的类别，最后实现类别划分。
收敛条件为所有的点都已经被划分到其中任意一个类别中了

很显然，有的点会被划分为多个类别

十一、层次聚类

与无监督的决策树类似
常用于存在包含关系的数据分类，例如：省市县等

Ⅰ分裂的层次聚类：DIANA

把原始数据集去不断的分裂，然后去计算每个子数据集里面的相似性，然后不断的分裂，把数据集分为很多的类别

Ⅱ凝聚的层次聚类：AGNES

把一个个样本，不断的自底向上的聚类，然后一层一层的来聚，最后聚成一个完整的数据集，这种用的更多一些

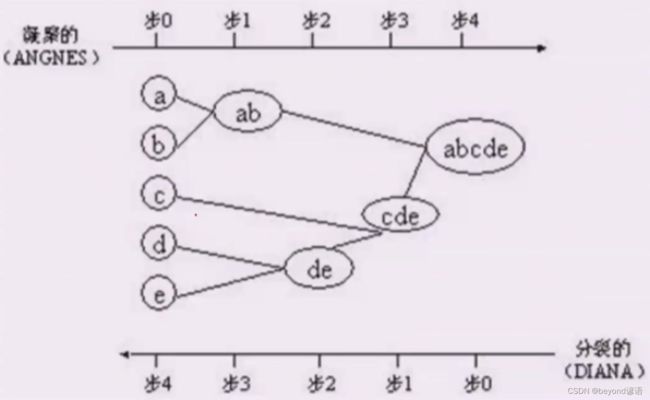
Ⅲ如何凝聚

如果两个样本，可以很好的度量距离，如果已经聚了一层，如何度量簇之间的相似性
①最小距离：两个簇中，最接近样本的距离，城市和城市边界最短距离，成链状一条线了
②最大距离：两个簇中，最远的样本的距离，某一个簇存在异常值就很麻烦，簇本身比较狭长
③平均距离：两两样本距离的平均、两两样本距离的平方和

十二、密度聚类

统计样本周边的密度，把密度给定一个阈值，不断的把样本添加到最近的簇
应用场景：人口密度，根据密度，聚类出城市
解决类似圆形的K-Means聚类的缺点，密度聚类缺点计算复杂度大，空间索引来降低计算时间，查找速度会有所降低
密度聚类可能会使得某个点没有任何类别

K-Means聚类针对的是圆形的，对于一些不规则的数据不好聚类，此时就可以通过密度聚类来进行弥补

Ⅰ，DBSCAN

Density Based Spatial Clustering of Applications with Noise
对象邻域：给定对象在半径内的区域

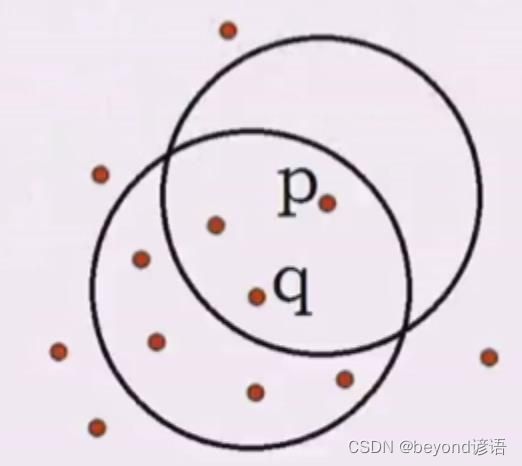
如果给定5为阈值，那么q是7，p是3，那么q是核心对象
而p是在q这个范围(制定一个半径)内的，那么说q到p是核心密度可达
q密度可达p1，p1密度可达p，那么q到p是密度可达

举例子，层次聚类
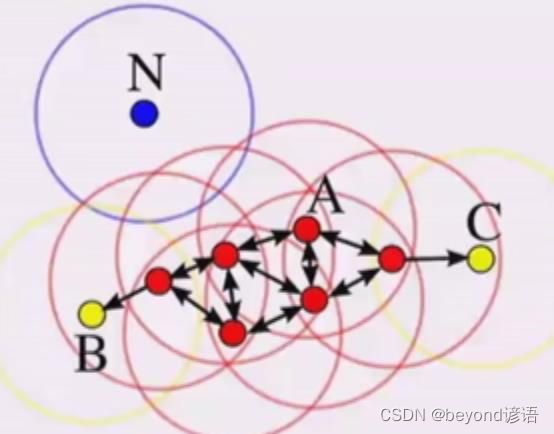
如果P密度可达A，B，C，那就把它们连接在一起
A可达E，F，B不是核心对象，C可达G
所有点都要进行是否是核心对象的判定
那么这些点同属于一个簇，最后没有更多样本可以加进来，这个时候扫描结束
不位于簇中的点就是噪声
K不需要给定，只给m个阈值，和半径r
一般常用作划分不规则区域，即非圆形

Ⅱ，密度可达

从o点能密度可达q，也能密度可达p，p和q叫密度相连

簇就是密度相连的最大的点的集合，即最大的密度相连构成的集合就是簇
如何一个点不是核心对象，也不能被别的点密度可达，就是噪声

Ⅲ，传入参数

给定的m个数不够，簇会变多，一般发生在边缘处

r=0.1，半径为0.1
m=5，一个圈内有5个点才算可以形成一个簇

r=0.1，半径为0.1
m=3，一个圈内有3个点才算可以形成一个簇

r=0.1，半径为0.1
m=2，一个圈内有2个点才算可以形成一个簇

不同的半径，r的值不同，太大就都聚到一块了

代码实现

# !/usr/bin/python
# -*- coding:utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler


def expand(a, b):
    d = (b - a) * 0.1
    return a-d, b+d


if __name__ == "__main__":
    N = 1000#1000个点
    centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]#人为给出聚类的中心点
    data, y = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=[0.5, 0.25, 0.7, 0.5], random_state=0)#y为类别号
    data = StandardScaler().fit_transform(data)#归一化(把数据进行相对应的缩放)，常见的有最大值最小值归一化、方差归一化、均值归一化
    # 数据的参数：(epsilon, min_sample)
    params = ((0.2, 5), (0.2, 10), (0.2, 15), (0.3, 5), (0.3, 10), (0.3, 15))

    matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
    matplotlib.rcParams['axes.unicode_minus'] = False

    plt.figure(figsize=(12, 8), facecolor='w')
    plt.suptitle(u'DBSCAN聚类', fontsize=20)

    for i in range(6):
        eps, min_samples = params[i]
        model = DBSCAN(eps=eps, min_samples=min_samples)
        model.fit(data)
        y_hat = model.labels_

        core_indices = np.zeros_like(y_hat, dtype=bool)
        core_indices[model.core_sample_indices_] = True

        y_unique = np.unique(y_hat)
        n_clusters = y_unique.size - (1 if -1 in y_hat else 0)
        print(y_unique, '聚类簇的个数为：', n_clusters)

        plt.subplot(2, 3, i+1)
        clrs = plt.cm.Spectral(np.linspace(0, 0.8, y_unique.size))
        print(clrs)
        for k, clr in zip(y_unique, clrs):
            cur = (y_hat == k)
            if k == -1:
                plt.scatter(data[cur, 0], data[cur, 1], s=20, c='k')
                continue
            plt.scatter(data[cur, 0], data[cur, 1], s=30, c=clr, edgecolors='k')
            plt.scatter(data[cur & core_indices][:, 0], data[cur & core_indices][:, 1], s=60, c=clr, marker='o', edgecolors='k')
        x1_min, x2_min = np.min(data, axis=0)
        x1_max, x2_max = np.max(data, axis=0)
        x1_min, x1_max = expand(x1_min, x1_max)
        x2_min, x2_max = expand(x2_min, x2_max)
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.grid(True)
        plt.title(u'epsilon = %.1f  m = %d，聚类数目：%d' % (eps, min_samples, n_clusters), fontsize=16)
    plt.tight_layout()
    plt.subplots_adjust(top=0.9)
    plt.show()

十三、谱和谱聚类

谱，通俗一点就是换个角度进行观察数据样本，例如从时域角度进行分析，其实就是多个正弦函数构成，这就相当于谱。

Ⅰ，谱

谱：Y=A*X，矩阵X乘以A等于对矩阵X做了空间线性变换，那么Y=map(X)，A就是map这个线性算
子，它的所有特征值的全体，称之为方阵的谱
方阵的谱半径为最大的特征值

Ⅱ，谱聚类

谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据进行聚类的目的

解决区域重叠问题，密度聚类对应区域重叠问题不太好办
有一堆个样本，可以构建成全连接图，并且两两样本之间总是可以去求相似度的
两两样本之间构建邻接矩阵来表示图

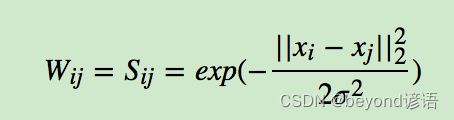
邻接矩阵上面的值，是用高斯相似度计算得来
然后对角线都是0，可以根据高斯相似度看出来，这样有了矩阵W
除了对角线都有相似度的值，然后把它们按行或列加和得对角阵D


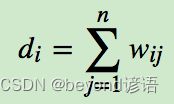
L=D-W，这样的L矩阵叫做Laplace矩阵
L矩阵是NN的，N是样本个数，实数形成的对数矩阵，求特征值和特征向量
Lui = lambda i*ui，lambda是特征值，ui是特征向量，一组lambda有从大到小可以排序
每个对应的lambda都对应一个ui，每个ui是一个个的列向量，比如u11,u21,u31,un1

根据排序默认从小到大，逆序之后我们就取前面的几个ui列向量就可以了，其实这是一种降维！
然后，前面的这几个列向量ui就成了新的对应每个样本的几个重要的特征！
最后，用K-Means聚类算法对样本进行聚类即可

代码实现

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors
from sklearn.cluster import spectral_clustering
from sklearn.metrics import euclidean_distances


def expand(a, b):
    d = (b - a) * 0.1
    return a-d, b+d


if __name__ == "__main__":
    matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
    matplotlib.rcParams['axes.unicode_minus'] = False

    t = np.arange(0, 2*np.pi, 0.1)
    data1 = np.vstack((np.cos(t), np.sin(t))).T
    data2 = np.vstack((2*np.cos(t), 2*np.sin(t))).T
    data3 = np.vstack((3*np.cos(t), 3*np.sin(t))).T
    data = np.vstack((data1, data2, data3))

    n_clusters = 3
    m = euclidean_distances(data, squared=True)
    sigma = np.median(m)

    plt.figure(figsize=(12, 8), facecolor='w')
    plt.suptitle(u'谱聚类', fontsize=20)
    clrs = plt.cm.Spectral(np.linspace(0, 0.8, n_clusters))
    for i, s in enumerate(np.logspace(-2, 0, 6)):
        print(s)
        af = np.exp(-m ** 2 / (s ** 2)) + 1e-6
        y_hat = spectral_clustering(af, n_clusters=n_clusters, assign_labels='kmeans', random_state=1)
        plt.subplot(2, 3, i+1)
        for k, clr in enumerate(clrs):
            cur = (y_hat == k)
            plt.scatter(data[cur, 0], data[cur, 1], s=40, c=clr, edgecolors='k')
        x1_min, x2_min = np.min(data, axis=0)
        x1_max, x2_max = np.max(data, axis=0)
        x1_min, x1_max = expand(x1_min, x1_max)
        x2_min, x2_max = expand(x2_min, x2_max)
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.grid(True)
        plt.title(u'sigma = %.2f' % s, fontsize=16)
    plt.tight_layout()
    plt.subplots_adjust(top=0.9)
    plt.show()