ccf-csp 2015秋季真题题解
- 数列分段
问题描述
给定一个整数数列,数列中连续相同的最长整数序列算成一段,问数列中共有多少段?
输入格式
输入的第一行包含一个整数n,表示数列中整数的个数。
第二行包含n个整数a1, a2, …, an,表示给定的数列,相邻的整数之间用一个空格分隔。
输出格式
输出一个整数,表示给定的数列有多个段。
样例输入
8
8 8 8 0 12 12 8 0
样例输出
5
样例说明
8 8 8是第一段,0是第二段,12 12是第三段,倒数第二个整数8是第四段,最后一个0是第五段。
评测用例规模与约定
1 ≤ n ≤ 1000,0 ≤ ai ≤ 1000。
代码:
#include - 日期计算
问题描述
给定一个年份y和一个整数d,问这一年的第d天是几月几日?
注意闰年的2月有29天。满足下面条件之一的是闰年:
1) 年份是4的整数倍,而且不是100的整数倍;
2) 年份是400的整数倍。
输入格式
输入的第一行包含一个整数y,表示年份,年份在1900到2015之间(包含1900和2015)。
输入的第二行包含一个整数d,d在1至365之间。
输出格式
输出两行,每行一个整数,分别表示答案的月份和日期。
样例输入
2015
80
样例输出
3
21
样例输入
2000
40
样例输出
2
9
题解:
和上一次考试 节日 那题一样,需要模拟日历,熟悉做法即可。
代码:
#include - 模板生成系统
问题描述
成成最近在搭建一个网站,其中一些页面的部分内容来自数据库中不同的数据记录,但是页面的基本结构是相同的。例如,对于展示用户信息的页面,当用户为 Tom 时,网页的源代码是

而当用户为 Jerry 时,网页的源代码是
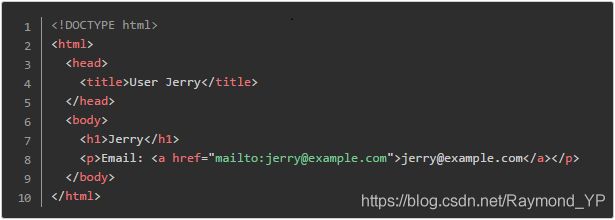
这样的例子在包含动态内容的网站中还有很多。为了简化生成网页的工作,成成觉得他需要引入一套模板生成系统。
模板是包含特殊标记的文本。成成用到的模板只包含一种特殊标记,格式为
,其中 VAR 是一个变量。该标记在模板生成时会被变量 VAR 的值所替代。例如,如果变量 name = “Tom”,则
会生成 Tom。具体的规则如下:
·变量名由大小写字母、数字和下划线 (_) 构成,且第一个字符不是数字,长度不超过 16 个字符。
·变量名是大小写敏感的,Name 和 name 是两个不同的变量。
·变量的值是字符串。
·如果标记中的变量没有定义,则生成空串,相当于把标记从模板中删除。
·模板不递归生成。也就是说,如果变量的值中包含形如
的内容,不再做进一步的替换。
输入格式
输入的第一行包含两个整数 m, n,分别表示模板的行数和模板生成时给出的变量个数。
接下来 m 行,每行是一个字符串,表示模板。
接下来 n 行,每行表示一个变量和它的值,中间用一个空格分隔。值是字符串,用双引号 (") 括起来,内容可包含除双引号以外的任意可打印 ASCII 字符(ASCII 码范围 32, 33, 35-126)。
输出格式
输出包含若干行,表示模板生成的结果。
样例输入
11 2
<html>
<head>
<title>User {{ name }}title>
head>
<body>
<h1>{{ name }}h1>
<p>Email: <a href="mailto:{{ email }}">{{ email }}a>p>
<p>Address:{{ address }}p>
body>
html>
name "David Beckham"
email "[email protected]"
样例输出
<html>
<head>
<title>User David Beckhamtitle>
head>
<body>
<h1>David Beckhamh1>
<p>Email: <a href="mailto:[email protected]">[email protected]a>p>
<p>Address: p>
body>
html>
评测用例规模与约定
0 ≤ m ≤ 100
0 ≤ n ≤ 100
输入的模板每行长度不超过 80 个字符(不包含换行符)。
输入保证模板中所有以 {{ 开始的子串都是合法的标记,开始是两个左大括号和一个空格,然后是变量名,结尾是一个空格和两个右大括号。
输入中所有变量的值字符串长度不超过 100 个字符(不包括双引号)。
保证输入的所有变量的名字各不相同。
题解:
首先把每一行句子存到vector
代码:
#include - 高速公路
问题描述
某国有n个城市,为了使得城市间的交通更便利,该国国王打算在城市之间修一些高速公路,由于经费限制,国王打算第一阶段先在部分城市之间修一些单向的高速公路。
现在,大臣们帮国王拟了一个修高速公路的计划。看了计划后,国王发现,有些城市之间可以通过高速公路直接(不经过其他城市)或间接(经过一个或多个其他城市)到达,而有的却不能。如果城市A可以通过高速公路到达城市B,而且城市B也可以通过高速公路到达城市A,则这两个城市被称为便利城市对。
国王想知道,在大臣们给他的计划中,有多少个便利城市对。
输入格式
输入的第一行包含两个整数n, m,分别表示城市和单向高速公路的数量。
接下来m行,每行两个整数a, b,表示城市a有一条单向的高速公路连向城市b。
输出格式
输出一行,包含一个整数,表示便利城市对的数量。
样例输入
5 5
1 2
2 3
3 4
4 2
3 5
样例输出
3
样例说明
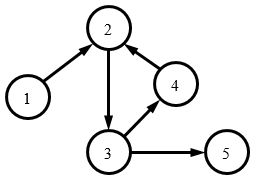
城市间的连接如图所示。有3个便利城市对,它们分别是(2, 3), (2, 4), (3, 4),请注意(2, 3)和(3, 2)看成同一个便利城市对。
评测用例规模与约定
前30%的评测用例满足1 ≤ n ≤ 100, 1 ≤ m ≤ 1000;
前60%的评测用例满足1 ≤ n ≤ 1000, 1 ≤ m ≤ 10000;
所有评测用例满足1 ≤ n ≤ 10000, 1 ≤ m ≤ 100000。
题解:
题目就是要求得有向图中的强连通分量,在每个强连通分量中,如果有 m 个城市,便利城市就对有 Cm2个。使用Tarjin算法来计算有向图中的强连通分量,关于tarjin算法的理解可以百度一下。
代码:
#include - 最佳文章
问题描述
小明最近在研究一门新的语言,叫做Q语言。Q语言单词和文章都可以用且仅用只含有小写英文字母的字符串表示,任何由这些字母组成的字符串也都是一篇合法的Q语言文章。
在Q语言的所有单词中,小明选出了他认为最重要的n个。使用这些单词,小明可以评价一篇Q语言文章的“重要度”。
文章“重要度”的定义为:在该文章中,所有重要的Q语言单词出现次数的总和。其中多次出现的单词,不论是否发生包含、重叠等情况,每次出现均计算在内。
例如,假设n = 2,小明选出的单词是gvagv和agva。在文章gvagvagvagv中,gvagv出现了3次,agva出现了2次,因此这篇文章的重要度为3+2=5。
现在,小明想知道,一篇由m个字母组成的Q语言文章,重要度最高能达到多少。
输入格式
输入的第一行包含两个整数n, m,表示小明选出的单词个数和最终文章包含的字母个数。
接下来n行,每行包含一个仅由英文小写字母构成的字符串,表示小明选出的这n个单词。
输出格式
输出一行一个整数,表示由m个字母组成的Q语言文章中,重要度最高的文章的重要度。
样例输入
3 15
agva
agvagva
gvagva
样例输出
11
样例说明
15个字母组成的重要度最高的文章为gvagvagvagvagva。
在这篇文章中,agva出现4次,agvagva出现3次,gvagva出现4次,共计4+3+4=11次。
评测用例规模与约定
在评测时将使用10个评测用例对你的程序进行评测。
设s为构成n个重要单词字母的总个数,例如在样例中,s=4+7+6=17;a为构成n个重要单词字母的种类数,例如在样例中,共有3中字母’a’,‘g’,‘v’,因此a=3。
评测用例1和2满足2 ≤ n ≤ 3,1500 ≤ m ≤ 2000,s = 40;
评测用例3和4满足m = 20,2 ≤ a ≤ 3;
评测用例5、6和7满足2000 ≤ m ≤ 100000;
评测用例8满足n = 2;
所有的评测用例满足1 ≤ s ≤ 100,1 ≤ m ≤ 1015,每个单词至少包含1个字母,保证单词中仅出现英文小写字母,输入中不含多余字符,不会出现重复的单词。
题解:
贴一道AC代码,源代码戳这里
代码:
#include