模式识别与机器学习课程笔记——决策树和贝叶斯估计

前言

    创新不是天马星空，无复盘不学习。

1 eager learner

1.1 Desicion Trees

1.1.1 第一个决策树：ID3算法

1.1.1.2 熵

熵：ID3决策树选择属性的依据；在热力学中，对于孤立的系统，任何自发进行的过程都不能使得系统的状态函数熵的总值减少（熵恒增定律）。

熵的含义：熵代表一个系统的混乱程度，对于一个孤立的系统，当发生可逆的过程的时候，熵增为零，当发生不可逆的过程的时候，熵增为正。

麦克斯韦妖（Maxwell’s demon）：1867年，麦克斯韦提出一个假说，就是在一个系统旁边有一个小妖怪，它知道所有粒子的运动状态和属性，而且这个系统中间插了一个带有一个小门孔的挡板。当这个小妖怪看准时机，打开小孔，“人”为的将系统两边的状态变的热的更热，冷的更冷。此时熵就减少了，因为热与冷统一了，混乱减少了。

负熵：上述麦克斯韦妖获得了分子的信息才使得系统的熵减少，我们称信息为负熵，信息的获取需要能量。

1.1.1.3 ID3实现举例

信息熵公式。

天气预报举例：根据天气判断能不能出去玩。

分支选择：

1. 首先是我们能够根据“规则”来判断哪些天气能够出去玩，yes or no。
   在任何初始树创建之前，我们是知道训练样本由9个yes和5个no。
   初始的信息熵为：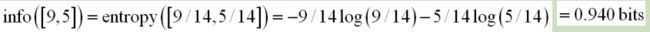

2. 再算出训练样本中各个天气属性的熵，这里以outlook为例：
   

3. 选择熵减少最多（初始熵-各个各个天气属性的熵）的属性作为第一个分支，因为我们的目的是熵减，熵减少越多我们得到的信息就越多，我们最后就能得到一个比较好的判断系统。
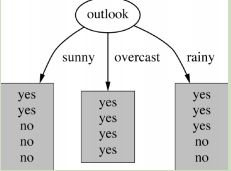
   这里以熵减少最多的outlook为例：
   
   

4. 建立分支
   

5. 继续分裂，我们现在要在sunny，overcast，rainy下继续分支，依然按照第一个分支所遵循的熵减最多规则。这里以sunny为例：就是所以天气属性为sunny的样本为一个数据集，对其进行如1-3步骤的处理。
   

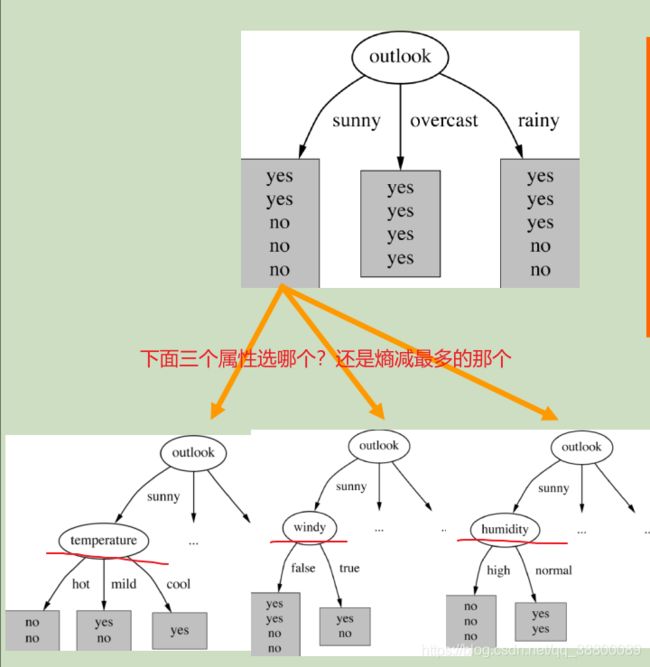
1.1.1.4 剪枝问题

在ID3算法中，计算信息增益时，由于信息增益存在一个内在偏置，它偏袒具有较多值的属性，太多的属性值把训练样例分割成非常小的空间。因此，这个属性可能会有非常高的信息增益，而且被选作树的根结点的决策属性，并形成一棵深度只为一级但却非常宽的树，这棵树可以理想地分类训练数据。但是这个决策树对于测试数据的分类性能可能会相当差（泛化能力较差），因为它过分地完美地分割了训练数据，不是一个好的分类器。

1.1.2 决策树的特点

1. 不需要特定领域的知识和参数设置，适合与探测式知识发现。
2. 大数据无法放入内存

1.1.3 其他决策树算法

1.1.4 决策树特点

1. 能充分利用领域知识和其它先验信息
2. 能进行增量学习，能处理不完整数据
3. 处理对象的属性一般是离散的

1.2 Bayesian

     话说贝叶斯是个牧师，这号人是相信上帝的，所以他的理论里会有一个先验概率。

1.2.1 朴素贝叶斯

它与贝叶斯网络的区别就是假定各个属性之间是独立的。

1.2.2 朴素贝叶斯举例Naïve Bayes Classifier (NB)

贝叶斯分类器的思路：就是用贝叶斯公式计算出测试样本属于各个类别的概率，然后选出概率最大的那个类别作为该测试样本的类别。

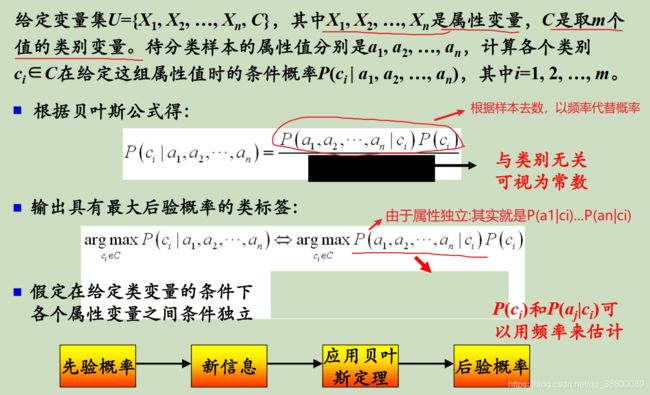
一个实例：

1.2.3 朴素贝叶斯举例Bayesian Decision

贝叶斯决策的前提：

1. 决策问题可以以概率分布的形式描述
2. 与决策有关的概率分布均是可计算的
   贝叶斯决策是要事先知道我决策类型的概率分布的（例如正态分布，平均分布，指数分布）。

1.2.3.1 最小错误率贝叶斯决策

最小错误率贝叶斯决策的目标是希望决策的平均错误率尽可能小。

定义错误率：

举例：假设一组训练数据符合正态分布，即满足贝叶斯决策的前提条件。

选择xc为决策边界（x>xc归为1类，反之归为2类，下同）的平均错误率：B+D+E+C
选择xb为决策边界的平均错误率：E+D+C
选择xa为决策边界的平均错误率：A+D+C+E
可以看到我们选择xb为决策边界比较合适。

1.2.3.2 最小风险贝叶斯决策

目的是希望平均损失最小，我们首先定义当判断错误了之后的风险函数，风险函数的定义是至关重要的，这也是和最小错误率贝叶斯决策的区别。比如将有病误判成无病的风险远远大于将无病误判成有病，因为前者是人的生命健康，后者是钱。

决策函数：决策函数就是根据风险最小来选择x的类别。
显然，最小风险贝叶斯决策选取使得条件风险最小的决策，同时该决策也会使得总体风险最小。

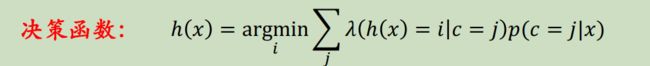
1.2.4 朴素贝叶斯举例Parameter Estimation

贝叶斯网络也可以用于参数估计，首先数据符合的模型是已知的，只是其中的参数需要进一步估计确定。

最大似然估计的方法：

最大后验估计的方法

贝叶斯参数估计：

1.3 Linear Regression

1.3.1 为何叫线性的

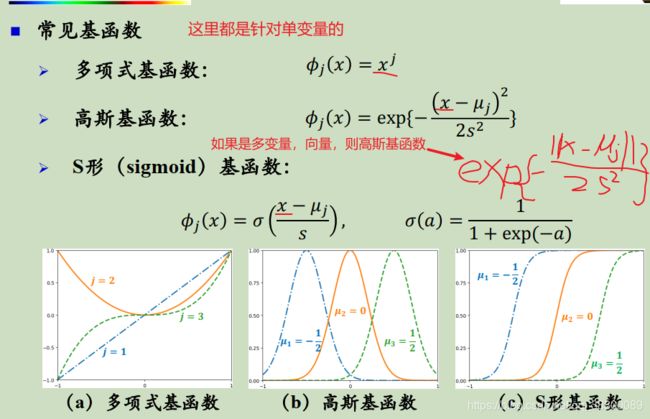
1.3.2 常见的基函数

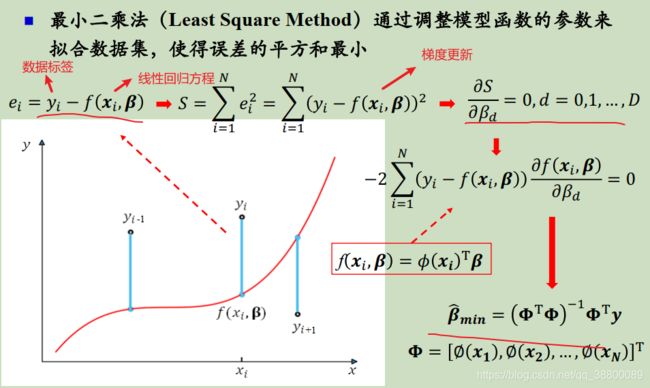
1.3.3训练方式：最小二乘法

1.3.4 解决过拟合

1.3 Logistic Regression（只有两种类别）

逻辑回归使用逻辑函数（两种类别输入进去得到的函数值相加等于1）和回归模型将分类目标转换成一个线性模型，返回值用于表示二分类问题中的概率。

这里我们用逻辑函数$\sigma (x)=\frac{e^x}{e^x+1}$

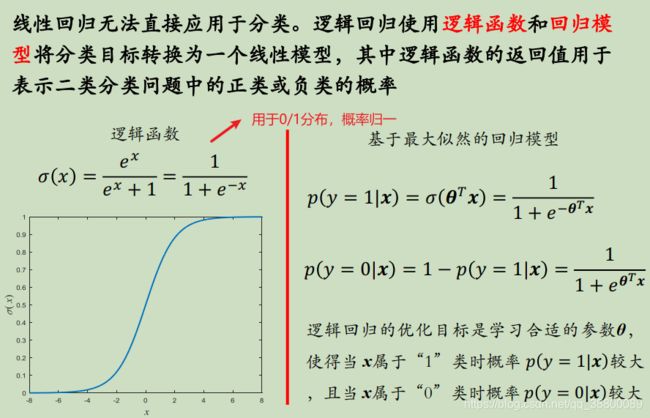
对于逻辑回归这种二分类问题，我们使用最大似然函数来进行参数的更新


线性回归是拟合输入向量 x 的分布，而逻辑回归中的线性函数是在拟合决策边界，它们的目标不一样，但同属于广义线性模型 GLM(Generalized Linear Models)，通过输入值 x 结合线性权重来预测输出值