Word2vec
链接:https://zhuanlan.zhihu.com/p/26306795
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1. 引子
大家好
我叫数据挖掘机
皇家布鲁斯特大学肄业
我喝最烈的果粒橙,钻最深的牛角尖
——执着如我
今天我要揭开Word2vec的神秘面纱
直窥其本质
相信我,这绝对是你看到的
最浅白易懂的 Word2vec 中文总结
(蛤?你问我为啥有这个底气?
且看下面,我的踩坑血泪史。。。)
2. Word2vec参考资料总结
(以下都是我踩过的坑,建议先跳过本节,阅读正文部分,读完全文回头再来看)
先大概说下我深挖 word2vec 的过程:先是按照惯例,看了 Mikolov 关于 Word2vec 的两篇原始论文,然而发现看完依然是一头雾水,似懂非懂,主要原因是这两篇文章省略了太多理论背景和推导细节;然后翻出 Bengio 03年那篇JMLR和 Ronan 11年那篇JMLR,看完对语言模型、用CNN处理NLP任务有所了解,但依然无法完全吃透 word2vec;这时候我开始大量阅读中英文博客,其中 北漂浪子 的一篇阅读量很多的博客吸引了我的注意,里面非常系统地讲解了 Word2vec 的前因后果,最难得的是深入剖析了代码的实现细节,看完之后细节方面了解了很多,不过还是觉得有些迷雾;终于,我在 quora 上看到有人推荐 Xin Rong 的那篇英文paper,看完之后只觉醍醐灌顶,酣畅淋漓,相见恨晚,成为我首推的 Word2vec 参考资料。下面我将详细列出我阅读过的所有 Word2vec 相关的参考资料,并给出评价
- Mikolov 两篇原论文:
- 『Distributed Representations of Sentences and Documents』
- 在前人基础上提出更精简的语言模型(language model)框架并用于生成词向量,这个框架就是 Word2vec
- 专门讲训练 Word2vec 中的两个trick:hierarchical softmax 和 negative sampling
- 北漂浪子的博客:『深度学习word2vec 笔记之基础篇』
- 优点:非常系统,结合源码剖析,语言平实易懂
- 缺点:太啰嗦,有点抓不住精髓
- Yoav Goldberg 的论文:『word2vec Explained- Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method』
- 优点:对 negative-sampling 的公式推导非常完备
- 缺点:不够全面,而且都是公式,没有图示,略显干枯
- Xin Rong 的论文:『word2vec Parameter Learning Explained』:
- !重点推荐!
- 理论完备由浅入深非常好懂,且直击要害,既有 high-level 的 intuition 的解释,也有细节的推导过程
- 一定要看这篇paper!一定要看这篇paper!一定要看这篇paper!
评论区告知了一条 沉重的信息,Rong Xin 于2017年驾驶飞机失事,永远离开了我们。缅怀,R.I.P,愿他能在天堂继续开心地科研@huichan
- 来斯惟的博士论文『基于神经网络的词和文档语义向量表示方法研究』以及他的博客(网名:licstar)
- 可以作为更深入全面的扩展阅读,这里不仅仅有 word2vec,而是把词嵌入的所有主流方法通通梳理了一遍
- 几位大牛在知乎的回答:『word2vec 相比之前的 Word Embedding 方法好在什么地方?』
- 刘知远、邱锡鹏、李韶华等知名学者从不同角度发表对 Word2vec 的看法,非常值得一看
- Sebastian 的博客:『On word embeddings - Part 2: Approximating the Softmax』
- 详细讲解了 softmax 的近似方法,Word2vec 的 hierarchical softmax 只是其中一种
3. 正文
你会在本文看到:
- 提纲挈领地讲解 word2vec 的理论精髓
- 学会用gensim训练词向量,并寻找相似词
你不会在本文看到
- 神经网络训练过程的推导
- hierarchical softmax/negative sampling 等 trick 的理论和实现细节
3.1. 什么是 Word2vec?
在聊 Word2vec 之前,先聊聊 NLP (自然语言处理)。NLP 里面,最细粒度的是 词语,词语组成句子,句子再组成段落、篇章、文档。所以处理 NLP 的问题,首先就要拿词语开刀。
举个简单例子,判断一个词的词性,是动词还是名词。用机器学习的思路,我们有一系列样本(x,y),这里 x 是词语,y 是它们的词性,我们要构建 f(x)->y 的映射,但这里的数学模型 f(比如神经网络、SVM)只接受数值型输入,而 NLP 里的词语,是人类的抽象总结,是符号形式的(比如中文、英文、拉丁文等等),所以需要把他们转换成数值形式,或者说——嵌入到一个数学空间里,这种嵌入方式,就叫词嵌入(word embedding),而 Word2vec,就是词嵌入( word embedding) 的一种
我在前作『都是套路: 从上帝视角看透时间序列和数据挖掘』提到,大部分的有监督机器学习模型,都可以归结为:
f(x)->y
在 NLP 中,把 x 看做一个句子里的一个词语,y 是这个词语的上下文词语,那么这里的 f,便是 NLP 中经常出现的『语言模型』(language model),这个模型的目的,就是判断 (x,y) 这个样本,是否符合自然语言的法则,更通俗点说就是:词语x和词语y放在一起,是不是人话。
Word2vec 正是来源于这个思想,但它的最终目的,不是要把 f 训练得多么完美,而是只关心模型训练完后的副产物——模型参数(这里特指神经网络的权重),并将这些参数,作为输入 x 的某种向量化的表示,这个向量便叫做——词向量(这里看不懂没关系,下一节我们详细剖析)。
我们来看个例子,如何用 Word2vec 寻找相似词:
- 对于一句话:『她们 夸 吴彦祖 帅 到 没朋友』,如果输入 x 是『吴彦祖』,那么 y 可以是『她们』、『夸』、『帅』、『没朋友』这些词
- 现有另一句话:『她们 夸 我 帅 到 没朋友』,如果输入 x 是『我』,那么不难发现,这里的上下文 y 跟上面一句话一样
- 从而 f(吴彦祖) = f(我) = y,所以大数据告诉我们:我 = 吴彦祖(完美的结论)
3.2. Skip-gram 和 CBOW 模型
上面我们提到了语言模型
- 如果是用一个词语作为输入,来预测它周围的上下文,那这个模型叫做『Skip-gram 模型』
- 而如果是拿一个词语的上下文作为输入,来预测这个词语本身,则是 『CBOW 模型』
3.2.1 Skip-gram 和 CBOW 的简单情形
我们先来看个最简单的例子。上面说到, y 是 x 的上下文,所以 y 只取上下文里一个词语的时候,语言模型就变成:
用当前词 x 预测它的下一个词 y
但如上面所说,一般的数学模型只接受数值型输入,这里的 x 该怎么表示呢? 显然不能用 Word2vec,因为这是我们训练完模型的产物,现在我们想要的是 x 的一个原始输入形式。
答案是:one-hot encoder
所谓 one-hot encoder,其思想跟特征工程里处理类别变量的 one-hot 一样(参考我的前作『数据挖掘比赛通用框架』、『深挖One-hot和Dummy背后的玄机』)。本质上是用一个只含一个 1、其他都是 0 的向量来唯一表示词语。
我举个例子,假设全世界所有的词语总共有 V 个,这 V 个词语有自己的先后顺序,假设『吴彦祖』这个词是第1个词,『我』这个单词是第2个词,那么『吴彦祖』就可以表示为一个 V 维全零向量、把第1个位置的0变成1,而『我』同样表示为 V 维全零向量、把第2个位置的0变成1。这样,每个词语都可以找到属于自己的唯一表示。
OK,那我们接下来就可以看看 Skip-gram 的网络结构了,x 就是上面提到的 one-hot encoder 形式的输入,y 是在这 V 个词上输出的概率,我们希望跟真实的 y 的 one-hot encoder 一样。

首先说明一点:隐层的激活函数其实是线性的,相当于没做任何处理(这也是 Word2vec 简化之前语言模型的独到之处),我们要训练这个神经网络,用反向传播算法,本质上是链式求导,在此不展开说明了,
当模型训练完后,最后得到的其实是神经网络的权重,比如现在输入一个 x 的 one-hot encoder: [1,0,0,…,0],对应刚说的那个词语『吴彦祖』,则在输入层到隐含层的权重里,只有对应 1 这个位置的权重被激活,这些权重的个数,跟隐含层节点数是一致的,从而这些权重组成一个向量 vx 来表示x,而因为每个词语的 one-hot encoder 里面 1 的位置是不同的,所以,这个向量 vx 就可以用来唯一表示 x。
注意:上面这段话说的就是 Word2vec 的精髓!!
此外,我们刚说了,输出 y 也是用 V 个节点表示的,对应V个词语,所以其实,我们把输出节点置成 [1,0,0,…,0],它也能表示『吴彦祖』这个单词,但是激活的是隐含层到输出层的权重,这些权重的个数,跟隐含层一样,也可以组成一个向量 vy,跟上面提到的 vx 维度一样,并且可以看做是词语『吴彦祖』的另一种词向量。而这两种词向量 vx 和 vy,正是 Mikolov 在论文里所提到的,『输入向量』和『输出向量』,一般我们用『输入向量』。
需要提到一点的是,这个词向量的维度(与隐含层节点数一致)一般情况下要远远小于词语总数 V 的大小,所以 Word2vec 本质上是一种降维操作——把词语从 one-hot encoder 形式的表示降维到 Word2vec 形式的表示。
3.2.2. Skip-gram 更一般的情形
上面讨论的是最简单情形,即 y 只有一个词,当 y 有多个词时,网络结构如下:
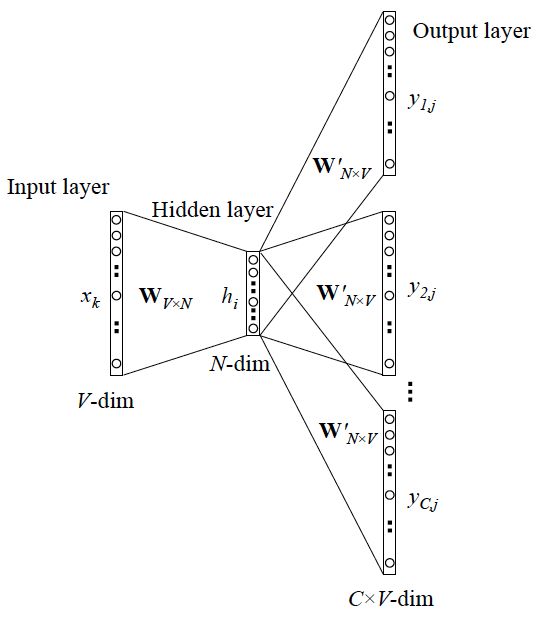
可以看成是 单个x->单个y 模型的并联,cost function 是单个 cost function 的累加(取log之后)
如果你想深入探究这些模型是如何并联、 cost function 的形式怎样,不妨仔细阅读参考资料4. 在此我们不展开。
3.2.3 CBOW 更一般的情形
跟 Skip-gram 相似,只不过:
Skip-gram 是预测一个词的上下文,而 CBOW 是用上下文预测这个词
网络结构如下
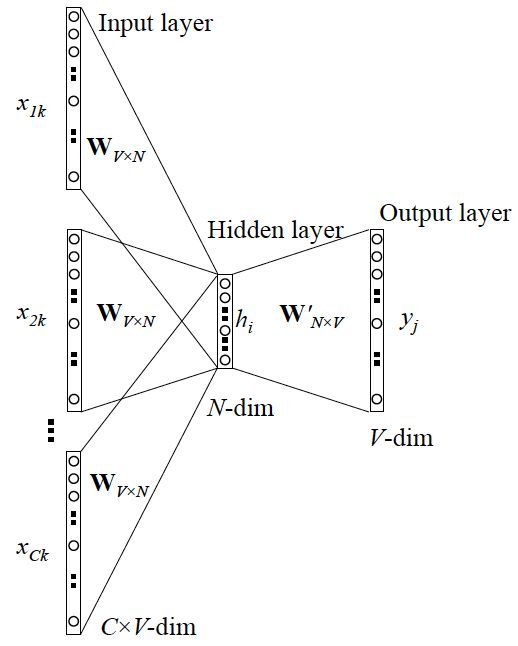
更 Skip-gram 的模型并联不同,这里是输入变成了多个单词,所以要对输入处理下(一般是求和然后平均),输出的 cost function 不变,在此依然不展开,建议你阅读参考资料4.
3.3. Word2vec 的训练trick
相信很多初次踩坑的同学,会跟我一样陷入 Mikolov 那篇论文(参考资料1.)里提到的 hierarchical softmax 和 negative sampling 里不能自拔,但其实,它们并不是 Word2vec 的精髓,只是它的训练技巧,但也不是它独有的训练技巧。 Hierarchical softmax 只是 softmax 的一种近似形式(详见参考资料7.),而 negative sampling 也是从其他方法借鉴而来。
为什么要用训练技巧呢? 如我们刚提到的,Word2vec 本质上是一个语言模型,它的输出节点数是 V 个,对应了 V 个词语,本质上是一个多分类问题,但实际当中,词语的个数非常非常多,会给计算造成很大困难,所以需要用技巧来加速训练。
这里我总结了一下这两个 trick 的本质,有助于大家更好地理解,在此也不做过多展开,有兴趣的同学可以深入阅读参考资料1.~7.
- hierarchical softmax
- 本质是把 N 分类问题变成 log(N)次二分类
- negative sampling
- 本质是预测总体类别的一个子集
3.4. 扩展
很多时候,当我们面对林林总总的模型、方法时,我们总希望总结出一些本质的、共性的东西,以构建我们的知识体系,比如我在前作『分类和回归的本质』里,原创性地梳理了分类模型和回归模型的本质联系,比如在词嵌入领域,除了 Word2vec之外,还有基于共现矩阵分解的 GloVe 等等词嵌入方法。
深入进去我们会发现,神经网络形式表示的模型(如 Word2vec),跟共现矩阵分解模型(如 GloVe),有理论上的相通性,这里我推荐大家阅读参考资料5. ——来斯惟博士在它的博士论文附录部分,证明了 Skip-gram 模型和 GloVe 的 cost fucntion 本质上是一样的。是不是一个很有意思的结论? 所以在实际应用当中,这两者的差别并不算很大,尤其在很多 high-level 的 NLP 任务(如句子表示、命名体识别、文档表示)当中,经常把词向量作为原始输入,而到了 high-level 层面,差别就更小了。
鉴于词语是 NLP 里最细粒度的表达,所以词向量的应用很广泛,既可以执行词语层面的任务,也可以作为很多模型的输入,执行 high-level 如句子、文档层面的任务,包括但不限于:
- 计算相似度
- 寻找相似词
- 信息检索
- 作为 SVM/LSTM 等模型的输入
- 中文分词
- 命名体识别
- 句子表示
- 情感分析
- 文档表示
- 文档主题判别
4. 实战
上面讲了这么多理论细节,其实在真正应用的时候,只需要调用 Gensim (一个 Python 第三方库)的接口就可以。但对理论的探究仍然有必要,你能更好地知道参数的意义、模型结果受哪些因素影响,以及举一反三地应用到其他问题当中,甚至更改源码以实现自己定制化的需求。
这里我们将使用 Gensim 和 NLTK 这两个库,来完成对生物领域的相似词挖掘,将涉及:
- 解读 Gensim 里 Word2vec 模型的参数含义
- 基于相应语料训练 Word2vec 模型,并评估结果
- 对模型结果调优
语料我已经放出来了,可以关注我的公众号『数据挖掘机养成记』,并回复 Sherlocked 获取语料,包含5000行生物医学领域相关文献的摘要(英文)
我将在下一篇文章里详细讲解实战步骤,敬请关注本人公众号。友情建议:请先自行安装 Gensim 和 NLTK 两个库,并建议使用 jupyter notebook 作为代码运行环境
欢迎各路大神猛烈拍砖,共同交流
====评论区答疑节选====
Q1. gensim 和 google的 word2vec 里面并没有用到onehot encoder,而是初始化的时候直接为每个词随机生成一个N维的向量,并且把这个N维向量作为模型参数学习;所以word2vec结构中不存在文章图中显示的将V维映射到N维的隐藏层。
A1. 其实,本质是一样的,加上 one-hot encoder 层,是为了方便理解,因为这里的 N 维随机向量,就可以理解为是 V 维 one-hot encoder 输入层到 N 维隐层的权重,或者说隐层的输出(因为隐层是线性的)。每个 one-hot encoder 里值是 1 的那个位置,对应的 V 个权重被激活,其实就是『从一个V*N的随机词向量矩阵里,抽取某一行』。学习 N 维向量的过程,也就是优化 one-hot encoder 层到隐含层权重的过程
Q2. hierarchical softmax 获取词向量的方式和原先的其实基本完全不一样,我初始化输入的也不是一个onehot,同时我是直接通过优化输入向量的形式来获取词向量?如果用了hierarchical 结构我应该就没有输出向量了吧?
A2. 初始化输入依然可以理解为是 one-hot,同上面的回答;确实是只能优化输入向量,没有输出向量了。具体原因,我们可以梳理一下不用 hierarchical (即原始的 softmax) 的情形:
隐含层输出一个 N 维向量 x, 每个x 被一个 N 维权重 w 连接到输出节点上,有 V 个这样的输出节点,就有 V 个权重 w,再套用 softmax 的公式,变成 V 分类问题。这里的类别就是词表里的 V 个词,所以一个词就对应了一个权重 w,从而可以用 w 作为该词的词向量,即文中的输出词向量。
PS. 这里的 softmax 其实多了一个『自由度』,因为 V 分类只需要 V-1 个权重即可
我们再看看 hierarchical softmax 的情形:
隐含层输出一个 N 维向量 x, 但这里要预测的目标输出词,不再是用 one-hot 形式表示,而是用 huffman tree 的编码,所以跟上面 V 个权重同时存在的原始 softmax 不一样, 这里 x 可以理解为先接一个输出节点,即只有一个权重 w1 ,输出节点输出 1/1+exp(-w*x),变成一个二分类的 LR,输出一个概率值 P1,然后根据目标词的 huffman tree 编码,将 x 再输出到下一个 LR,对应权重 w2,输出 P2,总共遇到的 LR 个数(或者说权重个数)跟 huffman tree 编码长度一致,大概有 log(V) 个,最后将这 log(V) 个 P 相乘,得到属于目标词的概率。但注意因为只有 log(V) 个权重 w 了,所以跟 V 个词并不是一一对应关系,就不能用 w 表征某个词,从而失去了词向量的意义
PS. 但我个人理解,这 log(V) 个权重的组合,可以表示某一个词。因为 huffman tree 寻找叶子节点的时候,可以理解成是一个不断『二分』的过程,不断二分到只剩一个词为止。而每一次二分,都有一个 LR 权重,这个权重可以表征该类词,所以这些权重拼接在一起,就表示了『二分』这个过程,以及最后分到的这个词的『输出词向量』。
我举个例子:
假设现在总共有 (A,B,C)三个词,huffman tree 这么构建:
第一次二分: (A,B), (C)
假如我们用的 LR 是二分类 softmax 的情形(比常见 LR 多了一个自由度),这样 LR 就有俩权重,权重 w1_1 是属于 (A,B) 这一类的,w1_2 是属于 (C) 的, 而 C 已经到最后一个了,所以 C 可以表示为 w1_2
第二次二分: (A), (B)
假设权重分别对应 w2_1 和 w2_2,那么 A 就可以表示为 [w1_1, w2_1], B 可以表示为 [w1_1, w2_2]
这样, A,B,C 每个词都有了一个唯一表示的词向量(此时他们长度不一样,不过可以用 padding 的思路,即在最后补0)
当然了,一般没人这么干。。。开个脑洞而已
Q3. 是否一定要用Huffman tree?
A3. 未必,比如用完全二叉树也能达到O(log(N))复杂度。但 Huffman tree 被证明是更高效、更节省内存的编码形式,所以相应的权重更新寻优也更快。 举个简单例子,高频词在Huffman tree中的节点深度比完全二叉树更浅,比如在Huffman tree中深度为3,完全二叉树中深度为5,则更新权重时,Huffmantree只需更新3个w,而完全二叉树要更新5个,当高频词频率很高时,算法效率高下立判