电机系列(1) - foc最基本原理、clark变换 、park变换、附代码
本文章更多的是,阅读别人的文章,再加上自己的理解和实践凑起来的
什么是FOC?
FOC(Field-Oriented Control),直译是磁场定向控制,也被称作矢量控制 (VC,Vector Control) ,是目前无刷直流电机(BLDC)和永磁同步电机(PMSM)高效控制的最优方法之一。FOC旨在通过精确地控制磁场大小与方向,使得电机的运动转矩平稳、噪声小、效率高,并且具有高速的动态响应。
简单来说就是,FOC是一种对无刷电机的驱动控制方法,它可以让我们对无刷电机进行 “像素级” 控制,实现很多传统电机控制方法所无法达到的效果。
因为所谓的“矢量控制”其实就是在做 解耦 ,把相互耦合的三相磁链解耦为容易控制的交轴 I q I_q Iq 和直轴 I d I_d Id 。整个过程就好比我们在做信号处理的时候,通过FFT把信号变换到频域进行处理之后再IFFT反变换回时域是一个道理。
FOC驱动器和无刷电调的区别
玩过航模的同学可能对无刷电机很熟悉,也应该知道航模中对于无刷电机的驱动使用的是 电子调速器(ESC) 也就是我们常说的电调,那么这个FOC驱动器和普通的电调有什么区别呢?
FOC的优势:
- 低转速下控制
由于控制原理的区别,无刷电调只能控制电机工作在高转速下,低速下无法控制;而FOC控制器则完全没有这个限制,不论在什么转速下都可以实现精确控制。 - 电机换向
同上面的理由,由于电调无法反馈转子位置,因此很难实现电机正反转的换向(当然有感电调可以实现);而FOC驱动器的换向性能极其优秀,最高转速下正反转切换可以非常顺畅;此外FOC还可以以能量回收的形式进行刹车控制。 - 力矩控制
普通电调都只能控制电机转速,而FOC可以进行电流(力矩)、速度、位置三个闭环控制。 - 噪音
FOC驱动器的噪音会比电调小很多,原因是普通电调采用方波驱动,而FOC是正弦波。
电调的优势:
- 兼容性
电调驱动不同的BLDC不需要进行参数整定,而FOC需要。 - 算法复杂度
电调的算法实现更简单,运算量少,很适合需要提高带宽的超高转速电机。 - 成本
电调的成本比FOC低很多。
综上大家应该可以看出来,FOC驱动器在控制性能上是要比电调强大得多的,其优异的性能和 磁场定向控制 的原理是密不可分的。
电机原理概述
基本物理知识准备
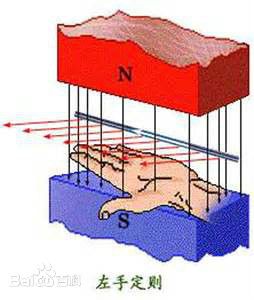
左手定则
百度百科
左手定则常用于判断通电导体在磁场中受力方向,由英国电机学工程师弗莱明提出。
导体受力 F ( N ) F(N) F(N) 为
F = I L B \LARGE F=ILB F=ILB
式中, B B B 为磁通量密度 ( W b / m 2 ) (Wb/m^2) (Wb/m2) ; I I I 为电流 ( A ) (A) (A) ; L L L 为处于磁场中的导体的长度 ( m ) (m) (m) 。
弗莱明右手定则 (又称发电机定则)
- 如右圖所示,右手三根手指互相垂直,大拇指的方向是 a / x / I \mathbf{a}/\mathbf{x}/\mathbf{I} a/x/I 的方向、食指的方向是 b / y / B \mathbf{b}/\mathbf{y}/\mathbf{B} b/y/B 的方向、中指的方向則為 c / z / F \mathbf{c}/\mathbf{z}/\mathbf{F} c/z/F 的方向。
右手定則可以用來找到力矩的方向。将右手掌张开,将四根手指从参考点朝着作用力的位置 r r r 指去,然后将大拇指伸开垂直于四根手指,再找到这四根手指与作用力 F F F 之间角度最小的夹角,将这四根手指弯扫过这夹角,则力矩矢量的方向是大拇指所指的方向。
-
拇指的方向是导体移动方向
-
食指的是磁场方向
-
中指的则为生成的电流方向
维基百科:中国教科书中的右手定则实为弗莱明右手定则的变体,而将这个定则叫做“右手螺旋定则”。
这个其实就是上面的 “左手定则” ,在国外可能是用“右手”表示。
右手定则
伸开右手,使大拇指跟其余四个手指垂直并且都跟手掌在一个平面内,把右手放入磁场中,让磁感线垂直穿入手心,大拇指指向导体运动方向,则其余四指指向感生电动势的方向。也就是切割磁感线的导体会产生反电动势,实际上通过反电动势定位转子位置也是普通无感电调工作的基础原理之一
右手螺旋定则 (又称安培定则)
百度百科
右手定则可以用于安培定律的两种互补应用方法:
-
螺线管载有的电流,会产生磁场。使用右手定则,可以判断磁场方向。将右手握住螺线管,四根手指朝着电流方向指去,然后将大拇指沿着螺线管的中心轴伸直,则磁场的方向即为大拇指所指的方向。

-
右手定则也可以用来辨明一条电线四周磁场的方向。对于这用法,右手定则称为“安培右手定则”,或“安培定则”。如右图所示,假若将右手的大拇指朝着电线的电流方向指去,再将其它四根手指握紧电线,则四根手指弯曲的方向为磁场的方向。

有刷、无刷电机
直流有刷电机简介
直流有刷电机通过换向器来改变电流方向,进而改变绕组的受力方向。由于其是机械换向,因此就带来一系列缺点,例如摩擦大,发热大,效率低等缺点
直流无刷电机简介
直流无刷电机通过使用电子器件代替机械换向,解决了直流有刷电机的缺点。为了便于分析我们将直流无刷电机抽象出上图模式,定子由三个线圈组成,转子由一对磁极组成。通过改变ABC三者电流方向来改变定子产生的磁场方向,从而使磁铁转动起来。
FOC控制原理
有感FOC步骤框图:
概括一下,FOC控制的整个过程是这样的:
- 对电机三相电流进行采样得到 I a , I b , I c I_{a}, I_{b}, I_{c} Ia,Ib,Ic
- 将 I a , I b , I c I_{a}, I_{b}, I_{c} Ia,Ib,Ic 经过
Clark变换得到 I α , I β I_{\alpha}, I_{\beta} Iα,Iβ - 将 I α , I β I_{\alpha}, I_{\beta} Iα,Iβ 经过
Park变换得到 I q , I d I_{q}, I_{d} Iq,Id - 计算 I q , I d I_{q}, I_{d} Iq,Id 和其设定值 I q − r e f , I d − r e f I_{q_{-}} r e f, I_{d_{-}} r e f Iq−ref,Id−ref 的误差
- 将上述误差输入两个PID(只用到PI)控制器,得到输出的控制电压 U q , U d U_q,U_d Uq,Ud
- 将 U q , U d U_q,U_d Uq,Ud 进行
反Park变换得到 U α , U β U_{\alpha}, U_{\beta} Uα,Uβ - 用 U α , U β U_{\alpha}, U_{\beta} Uα,Uβ 合成电压空间矢量,输入
SVPWM模块进行调制,输出该时刻三个半桥的状态编码值(前文有提到) - 按照前面输出的编码值控制三相逆变器的 MOS 管开关,驱动电机
- 循环上述步骤
变换
Clarke变换
clark变换:将 a b c \large abc abc 变换到 静止 的 α β \large \alpha \beta αβ 坐标系下。
三相对称正弦电流的大小可以这样表示:
{ I a = I m cos ( ω t ) I b = I m cos ( ω t − 2 π 3 ) I c = I m cos ( ω t + 2 π 3 ) \large \left\{\begin{matrix} I_a =& I_m \cos( \omega t) \\ I_b =& I_m \cos( \omega t - \frac{2\pi}{3}) \\ I_c =& I_m \cos( \omega t + \frac{2\pi}{3}) \\ \end{matrix}\right. ⎩⎪⎨⎪⎧Ia=Ib=Ic=Imcos(ωt)Imcos(ωt−32π)Imcos(ωt+32π)
其中, I m \large I_m Im 标识赋值; ω = 2 π f \large \omega = 2\pi f ω=2πf 标识角速度,三项电流在空间上互差120° 。
三相电流的矢量表达和合成矢量可以这样表达:
{ I a → = I a ⋅ e 0 I b → = I b ⋅ e − j 2 π 3 I c → = I c ⋅ e j 2 π 3 I s → = I a → + I b → + I c → \large \left\{\begin{matrix} \overrightarrow{I_a} =& I_a \cdot e^0 \\ \overrightarrow{I_b} =& I_b \cdot e^{-j \frac{2\pi}{3}} \\ \overrightarrow{I_c} =& I_c \cdot e^{j \frac{2\pi}{3}} \\ \end{matrix}\right. \\\\ \large \overrightarrow{I_s} = \overrightarrow{I_a} + \overrightarrow{I_b} + \overrightarrow{I_c} ⎩⎪⎪⎪⎨⎪⎪⎪⎧Ia=Ib=Ic=Ia⋅e0Ib⋅e−j32πIc⋅ej32πIs=Ia+Ib+Ic
所以 I s → \large \overrightarrow{I_s} Is 就等于
I s → = I m cos ( ω t ) + I m cos ( ω t − 2 π 3 ) ⋅ e − j 2 π 3 + I m cos ( ω t + 2 π 3 ) ⋅ e j 2 π 3 \large \overrightarrow{I_s} = I_m \cos( \omega t) + I_m \cos( \omega t - \frac{2\pi}{3}) \cdot e^{-j \frac{2\pi}{3}} + I_m \cos( \omega t + \frac{2\pi}{3}) \cdot e^{j \frac{2\pi}{3}} Is=Imcos(ωt)+Imcos(ωt−32π)⋅e−j32π+Imcos(ωt+32π)⋅ej32π
根据 欧拉公式 e j x = cos x + j sin x \large e^{jx} = \cos x+j\sin x ejx=cosx+jsinx ,可以推出:
I s → = I m cos ( ω t ) + I m cos ( ω t − 2 π 3 ) ( cos ( 2 π 3 ) + j sin ( 2 π 3 ) ) + I m cos ( ω t + 2 π 3 ) ( cos ( 2 π 3 ) − j sin ( 2 π 3 ) ) \large \begin{array}{rc} \overrightarrow{I_{s}}=\quad & I_{m} \cos (\omega t)+\\ & I_{m} \cos \left(\omega t-\frac{2 \pi}{3}\right)\left(\cos \left(\frac{2 \pi}{3}\right)+j \sin \left(\frac{2 \pi}{3}\right)\right)+\\ & I_{m} \cos \left(\omega t+\frac{2 \pi}{3}\right)\left(\cos \left(\frac{2 \pi}{3}\right)-j \sin \left(\frac{2 \pi}{3}\right)\right) \end{array} Is=Imcos(ωt)+Imcos(ωt−32π)(cos(32π)+jsin(32π))+Imcos(ωt+32π)(cos(32π)−jsin(32π))
进一步化简可得:
I s → = I m cos ( ω t ) + I m [ cos ( ω t ) cos ( 2 π 3 ) + sin ( ω t ) sin ( 2 π 3 ) ] ( − 1 2 + j 3 2 ) + I m [ cos ( ω t ) cos ( 2 π 3 ) − sin ( ω t ) sin ( 2 π 3 ) ] ( − 1 2 − j 3 2 ) \large \begin{array}{rc} \overrightarrow{I_{s}}= & I_{m} \cos (\omega t)+ \\ & I_{m}\left[\cos (\omega t) \cos \left(\frac{2 \pi}{3}\right)+\sin (\omega t) \sin \left(\frac{2 \pi}{3}\right)\right]\left(-\frac{1}{2}+j \frac{\sqrt{3}}{2}\right)+ \\ & I_{m}\left[\cos (\omega t) \cos \left(\frac{2 \pi}{3}\right)-\sin (\omega t) \sin \left(\frac{2 \pi}{3}\right)\right]\left(-\frac{1}{2}-j \frac{\sqrt{3}}{2}\right) \end{array} Is=Imcos(ωt)+Im[cos(ωt)cos(32π)+sin(ωt)sin(32π)](−21+j23)+Im[cos(ωt)cos(32π)−sin(ωt)sin(32π)](−21−j23)
代入三角函数值可得:
I s → = I m cos ( ω t ) + I m [ − 1 2 cos ( ω t ) + 3 2 sin ( ω t ) ] ( − 1 2 + j 3 2 ) + I m [ − 1 2 cos ( ω t ) − 3 2 sin ( ω t ) ] ( − 1 2 − j 3 2 ) \large \begin{array}{rc} \overrightarrow{I_{s}}= & I_{m} \cos (\omega t)+ \\ & I_{m}\left[-\frac{1}{2} \cos (\omega t)+\frac{\sqrt{3}}{2} \sin (\omega t)\right]\left(-\frac{1}{2}+j \frac{\sqrt{3}}{2}\right)+ \\ & I_{m}\left[-\frac{1}{2} \cos (\omega t)-\frac{\sqrt{3}}{2} \sin (\omega t)\right]\left(-\frac{1}{2}-j \frac{\sqrt{3}}{2}\right) \end{array} Is=Imcos(ωt)+Im[−21cos(ωt)+23sin(ωt)](−21+j23)+Im[−21cos(ωt)−23sin(ωt)](−21−j23)
最后化简得到:
I s → = 3 2 I m cos ( ω t ) + j 3 2 I m sin ( ω t ) \large \overrightarrow{I_s} = \frac{3}{2}I_m\cos(\omega t ) + j\frac{3}{2}I_m \sin(\omega t) Is=23Imcos(ωt)+j23Imsin(ωt)
既:
I s → = 3 2 I m e − j ω t \large \overrightarrow{I_s} = \frac{3}{2}I_m e^{-j \omega t} Is=23Ime−jωt
可以看出,三相对称正弦电流的合成矢量的一个角速度为 ω \large \omega ω ,绕中心点旋转的矢量,因此能形成旋转磁场。它的幅值为单相幅值的 3 2 \large \frac{3}{2} 23 倍。
进一步,我们将 a b c abc abc 变换到 静止 的 α − β \large \alpha - \beta α−β 坐标系下,我们可以得到
{ I α = I a − I b cos π 3 − I c cos π 3 I β = I b cos π 6 − I c cos π 6 \large \left\{\begin{array}{rc} I_{\alpha}= & I_{a}-I_{b} \cos \frac{\pi}{3}-I_{c} \cos \frac{\pi}{3} \\ I_{\beta} = & I_{b} \cos \frac{\pi}{6}-I_{c} \cos \frac{\pi}{6} \end{array}\right. {Iα=Iβ=Ia−Ibcos3π−Iccos3πIbcos6π−Iccos6π
将上式写为矩阵形式:
[ I α I β ] = k [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ I a I b I c ] \large \begin{bmatrix} I_{\alpha }\\ I_{\beta } \end{bmatrix} =k\begin{bmatrix} 1 &-\frac{1}{2} &-\frac{1}{2} \\ 0&\frac{\sqrt{3}}{2} &-\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} I_{a}\\ I_{b}\\ I_{c} \end{bmatrix} [IαIβ]=k[10−2123−21−23]⎣⎢⎡IaIbIc⎦⎥⎤
-
若 k = 2 3 \large k=\sqrt\frac{2}{3} k=32 ,变换前后,功率不变。又称为: Concordia变换
-
若 k = 2 3 \large k=\frac{2}{3} k=32 ,变换前后,幅值不变,(既合成矢量的大小和方向相等)。
⭐️根据基尔霍夫电流定律 I a + I b + I c = 0 \large I_a + I_b + I_c = 0 Ia+Ib+Ic=0 ,然后为了保证幅值不变把 k = 2 3 \large k=\frac{2}{3} k=32 带入,上述式子继续化简,最后可以得到
{ I α = I a I β = 1 3 I a + 2 3 I b \large \left\{\begin{matrix} I_{\alpha } &=& I_a \\ I_{\beta } &=& \frac{1}{\sqrt{3}}I_a + \frac{2}{\sqrt{3}}I_b \end{matrix}\right. {IαIβ==Ia31Ia+32Ib
然后我们再来看看 功率不变 情况,也就是 k = 2 3 \large k=\sqrt\frac{2}{3} k=32 时,假设变换前的功率为 P 0 \large P_0 P0 ,变换后的功率为 P 1 \large P_1 P1 ,那么有
P 0 = U m × I m × 3 P 1 = 2 3 U m × k × 2 3 I m × k × 2 \large \begin{array}{rlc} P_{0} & = U_{m} \times I_{m} \times 3 \\ P_{1} & =\frac{2}{3} U_{m} \times k \times \frac{2}{3} I_{m} \times k \times 2 \end{array} P0P1=Um×Im×3=32Um×k×32Im×k×2
但 k = 2 3 \large k=\sqrt\frac{2}{3} k=32 时, P 0 = P 1 \large P_0 = P_1 P0=P1 ,也就是功率不变
Park变换
这一步中我们接着Clark变换将 α − β \large \alpha - \beta α−β 坐标系旋转 θ 度,其中 θ 是转子当前的角度,如下图:
变换公式如下:
{ I d = I α cos ( θ ) + I β sin ( θ ) I q = − I α sin ( θ ) + I β cos ( θ ) \large \left\{\begin{array}{l} I_{d}=I_{\alpha} \cos (\theta)+I_{\beta} \sin (\theta) \\ I_{q}=-I_{\alpha} \sin (\theta)+I_{\beta} \cos (\theta) \end{array}\right. {Id=Iαcos(θ)+Iβsin(θ)Iq=−Iαsin(θ)+Iβcos(θ)
⭐️也很简单,就是作用了一个旋转矩阵 ,写成矩阵形式:
[ I d I q ] = [ cos θ sin θ − sin θ cos θ ] [ I α I β ] \large \left[\begin{array}{c} I_{d} \\ I_{q} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c} I_{\alpha} \\ I_{\beta} \end{array}\right] [IdIq]=[cosθ−sinθsinθcosθ][IαIβ]
也就是说,这个 d − q d-q d−q 坐标系是始终跟着转子旋转的!
- d d d 轴方向与转子磁链方向重合,又叫直轴
- q q q 轴方向与转子磁链方向垂直,又叫交轴
这个操作是可行的,因为我们会通过编码器输入转子的实时旋转角度,所以这个角度始终是一个已知数。经过这一步的变换,我们会发现,一个匀速旋转向量在这个坐标系下变成了一个定值!(显然的嘛,因为参考系相对于该向量静止了),这个坐标系下两个控制变量都被线性化了!
接下来如果我们以 I q , I d I_q, I_d Iq,Id 这两个值作为反馈控制的对象,那么显然就可以使用一些线性控制器来进行控制了,比如PID(是的,尽管学术界有很多炫酷的高级控制方法, 但是工业界还是偏爱PID)。
至此我们已经理解完上面FOC控制过程9个步骤的前3步了。
Clarke Park 变换测试
上位机用的是 “VOFA+”
模拟三相电流(红色、绿色和蓝色)
经过 Clarke变换 的波形(紫色和橙色)
经过 Park 变换 的波形(粉色和黄色)
说明
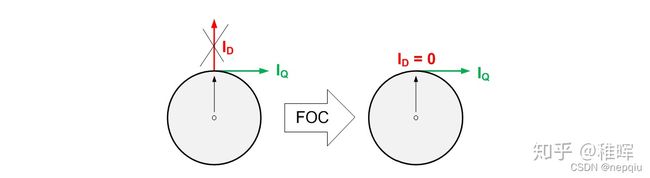
特别说明一下其中的 I q , I d , I q _ r e f , I d _ r e f \LARGE I_q,I_d, I_{q\_ref}, I_{d\_ref} Iq,Id,Iq_ref,Id_ref ,前两者大家知道是通过Clark变换和Park变换得到的,而后两者是我们预期希望前两者达到的值,这个值具体代表了什么物理量呢?参考一下下图:
也就是说我们一通操作将转子磁链进行了解耦,分解为了转子旋转的径向和切向这两个方向的变量:
- 其中 I q \LARGE I_q Iq 是我们需要的,代表了期望的力矩输出
- 而 I d \LARGE I_d Id 是我们不需要的,一般我们希望尽可能把它控制为0
FOC的控制目标通过PID控制器使用上述输入(电流采样值、编码器位置)和输出(MOS管开关状态)完成对电机电流的闭环控制。
代码
clark
/*-----------------------------------------------------------------------------
CLARKE 变换 宏
-----------------------------------------------------------------------------*/
#define CLARKE_DEFAULTS \
{ 0, 0, 0, 0, 0 }
#define CLARK_ONEbySQRT3 0.57735026918963f /* 1/sqrt(3) */
#define CLARK_ONEbyTHREE 0.33333333333333f /* 1/3 */
/* 为1的话是虚假的三电流输入,本质上还是两电流,为0的话是不用电流相加为0这个公式来计算clark */
#define CLARK_3_current 1
/*-----------------------------------------------------------------------------
CLARKE 变换 结构体
-----------------------------------------------------------------------------*/
typedef struct {
fp32 As; //!< Input: phase-a stator variable
fp32 Bs; //!< Input: phase-b stator variable
fp32 Cs; //!< Input: phase-c stator variable
fp32 Alpha; //!< Output: stationary d-axis stator variable
fp32 Beta; //!< Output: stationary q-axis stator variable
} clarke_t;
/*------------------------------------------------------------------------------
CLARKE 变换 变量
------------------------------------------------------------------------------*/
static const fp32 _onebysqrt3 = (CLARK_ONEbySQRT3);
static const fp32 _onebythree = (CLARK_ONEbyTHREE);
/*------------------------------------------------------------------------------
CLARKE 变换 函数实体
------------------------------------------------------------------------------*/
/**
* @brief clarke变换
* @param[in] *v: clarke_t结构体
* @param[in] _A: ABC坐标系下的电流a
* @param[in] _B: ABC坐标系下的电流b
* @param[out] v->Alpha: Alpha Beta坐标系下的电流Alpha
* v->Beta: Alpha Beta坐标系下的电流Beta
* @retval none
* @attention 输入两电流
*/
static inline void clarke_calc_2(clarke_t* v, fp32 _A, fp32 _B) {
v->As = _A;
v->Bs = _B;
v->Alpha = v->As;
v->Beta = (v->As + (v->Bs * 2.0f)) * _onebysqrt3;
}
/**
* @brief clarke变换
* @param[in] *v: clarke_t结构体
* @param[in] _A: ABC坐标系下的电流a
* @param[in] _B: ABC坐标系下的电流b
* @param[in] _C: ABC坐标系下的电流c
* @param[out] v->Alpha: Alpha Beta坐标系下的电流Alpha
* v->Beta: Alpha Beta坐标系下的电流Beta
* @retval none
* @attention 输入三电流
*/
static inline void clarke_calc_3(clarke_t* v, fp32 _A, fp32 _B, fp32 _C) {
v->As = _A;
v->Bs = _B;
v->Cs = _C;
#if (CLARK_3_current == 1)
v->Alpha = v->As;
v->Beta = (v->Bs - v->Cs) * _onebysqrt3;
#elif (CLARK_3_current == 0)
v->Alpha = (2 * v->As - v->Bs - v->Cs) * _onebythree;
v->Beta = (v->Bs - v->Cs) * _onebysqrt3;
#endif
}
park
/*-----------------------------------------------------------------------------
PARK 变换 宏
-----------------------------------------------------------------------------*/
#define PARK_DEFAULTS \
{ 0, 0, 0, 0, 0, 0, 0, }
/*-----------------------------------------------------------------------------
PARK 变换 结构体
-----------------------------------------------------------------------------*/
typedef struct {
fp32 Alpha; //!< Input: stationary d-axis stator variable
fp32 Beta; //!< Input: stationary q-axis stator variable
fp32 Angle; //!< Input: rotating angle (pu)
fp32 Ds; //!< Output: rotating d-axis stator variable
fp32 Qs; //!< Output: rotating q-axis stator variable
fp32 Sine; //!< Input: Sine term
fp32 Cosine; //!< Input: Cosine term
} park_t;
/*------------------------------------------------------------------------------
PARK 变换 函数实体
------------------------------------------------------------------------------*/
/**
* @brief park变换
* @param[in] *v: park_t结构体
* @param[in] _Alpha: Alpha Beta坐标系下的电流Alpha
* @param[in] _Beta: Alpha Beta坐标系下的电流Beta
* @param[out] v->Ds: dq坐标系下的电流d
* v->Qs: dq坐标系下的电流q
* @retval none
*/
static inline void park_calc(park_t* v, fp32 _Alpha, fp32 _Beta, fp32 _Angle) {
fp32 cosTh, sinTh;
v->Alpha = _Alpha;
v->Beta = _Beta;
v->Angle = _Angle;
sinTh = falst_sin(v->Angle);
cosTh = falst_cos(v->Angle);
v->Ds = (v->Alpha * cosTh) + (v->Beta * sinTh);
v->Qs = (v->Beta * cosTh) - (v->Alpha * sinTh);
}
ipark
/*-----------------------------------------------------------------------------
IPARK 变换 宏
-----------------------------------------------------------------------------*/
#define IPARK_DEFAULTS \
{ 0, 0, 0, 0, 0, 0, 0, }
/*------------------------------------------------------------------------------
IPARK 变换 结构体
------------------------------------------------------------------------------*/
typedef struct {
fp32 Alpha; //!< Output: stationary d-axis stator variable
fp32 Beta; //!< Output: stationary q-axis stator variable
fp32 Angle; //!< Input: rotating angle (pu)
fp32 Ds; //!< Input: rotating d-axis stator variable
fp32 Qs; //!< Input: rotating q-axis stator variable
fp32 Sine; //!< Input: Sine term
fp32 Cosine; //!< Input: Cosine term
} ipark_t;
/*------------------------------------------------------------------------------
IPARK 变换 函数实体
------------------------------------------------------------------------------*/
/**
* @brief ipark变换
* @param[in] *v: ipark_t结构体
* @param[in] _Ds: dq坐标系下的电流d
* @param[in] _Qs: dq坐标系下的电流q
* @param[out] v->Alpha: Alpha Beta坐标系下的电流Alpha
* v->Beta: Alpha Beta坐标系下的电流Beta
* @retval none
*/
static inline void ipark_calc(ipark_t* v, fp32 _Ds, fp32 _Qs, fp32 _Angle) {
fp32 Cosine, Sine;
v->Ds = _Ds;
v->Qs = _Qs;
v->Angle = _Angle;
Sine = falst_sin(v->Angle);
Cosine = falst_cos(v->Angle);
v->Alpha = (v->Ds * Cosine) - (v->Qs * Sine);
v->Beta = (v->Qs * Cosine) + (v->Ds * Sine);
}
参考、引用
- 【自制FOC驱动器】深入浅出讲解FOC算法与SVPWM技术
- 手撕系列(2):Clark变换与Park变换
- Clark变换与Park(派克)变换
- FOC:在MCU上检验Clark和Park坐标变换是否正确
- FOC中的Clarke变换和Park变换详解(动图+推导+仿真+附件代码)
- FOC入门教程 和 嘉立创上的开源的板子(有代码地址)