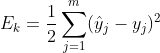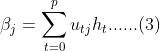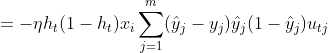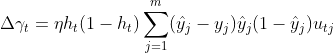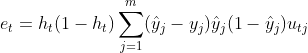深度学习笔记（二）——从多层感知机模型（MLP）到人工神经网络模型（ANN）

一、人工神经网络定义

        广义上来说，由神经元模型构成的模型就可以称之为人工神经网络模型。神经元模型已经在上一篇感知机的笔记中进行介绍。上一篇也提到，两层神经元模型即可组成最简单的感知机模型，其中第一层称为输入层，第二层称为输出层。由于单层感知机的学习能力限制，科研人员又提出将多个感知机组合到一起，构成了多层感知机（Multilayer Perceptron）模型。本文主要来介绍最基础的人工神经网络模型——多层感知机模型。

二、多层感知机模型

        在神经网络模型中，将信号逐层向前传播的神经网络称为前馈网络，感知机模型就是典型的前馈网络。而多个感知机模型排列而成的多层感知机模型也是前馈网络，也可以具体称为多层前馈网络（Multi-Layer FeedForward Neural Networks）。在多层感知机中，每一层的各个神经元的输出都会传到下一层的各个神经元中，因此多层感知机也称为全连接网络。

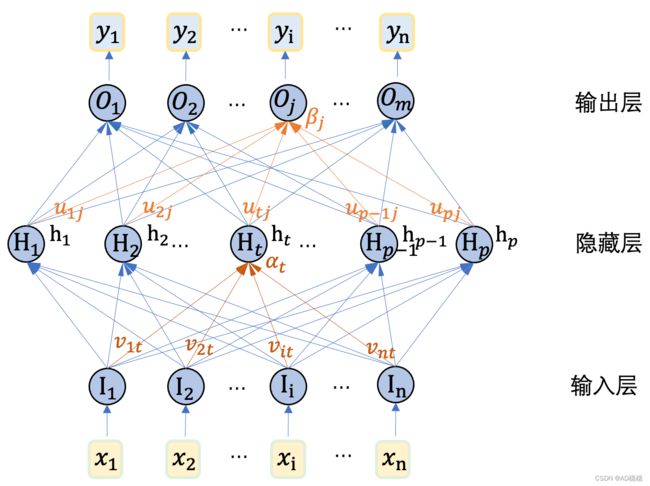
        由于多层感知机模型由多个感知机模型连接形成，因此，相邻两个感知机模型中，第一个感知机模型的输入即为第二个感知机模型的输入，因此第二个感知机模型的输入层可以省略掉不进行表示。在多层感知机中，除了整体模型的输入层和输出层之外，中间的各层都称为隐藏层（Hidden Layer）。下图是一个包含两层感知机的双层感知机模型，由于该模型包含一个隐藏层，也称为单隐藏层MLP。

        在该图中，n表示输入数据的维度，m表示输出数据的维度，p表示隐藏层的维度；在这个双层MLP中，输入变量为向量，输出向量为; 表示输入层的第个神经元模型、表示隐藏层第个神经元模型、表示输出层第个神经元；权重表示输入层神经元到隐藏层神经元之间的权重、权重表示神经元到神经元之间的权重；由输入数据和权重可以得到，隐藏层神经元的输入数据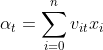，再结合激活函数，隐藏层神经元的输出值为，其中函数为激活函数，表示神经元的阈值；类似地，输出层神经元的输入数据即为，可以得到输出神经元的输出数据为，其中函数为激活函数，为神经元的阈值。

三、双层感知机模型的学习

（一）、待学习参数数量

        由于MLP是由多个感知机模型组合构成的，整体模型的待学习参数即为每层感知机的参数量之和。每个单层感知机模型中待学习的参数为输出层与输入层的所有连接权重，及每个输出层神经元的阈值，其中阈值数量为输入层神经元数X输出层神经元数，阈值数等于输出层神经元数。同样，在多层感知机中，需要计算的包括所有相邻两层的连接权重，及所有隐藏层及输出层的阈值。

        计算上图中表示的双层感知机，需要学习的参数量即为: 

（二）、参数学习算法(误差逆传播算法——BP算法[Error BackPropagation])

        本节来学习前馈网络中最常用也是最经典的BP算法，来研究多层感知机的参数学习算法。以前面提到的双层MLP模型为例。首先，定义模型的训练数据集中的某一个数据元组为，其中为数据自变量，为该自变量对应的真实值。假设当前MLP模型对输入数据给出的预测值为，模型中应用的激活函数、均为Sigmoid函数，针对数据预测误差采用均方误差进行计算，即

。

        在双层感知机模型中，共有个参数需要确定，对于每一个参数，我们均采用单层感知机中类似的方式进行参数更新，即对任意一个参数，其中即为每轮学习参数的更新量。

        一下以隐藏层神经元与输出层神经元之间的连接权重的更新为例。BP算法基于梯度下降策略进行更新参数，即以目标的负梯度方向进行更新。根据误差进行反向梯度计算，假设学习率为，则：

其中，公式(1)为误差对参数计算的偏导数，考虑到从误差计算参数需先计算输出层神经元输出值及输出层神经元输入值，因此可以得到完整路径的偏导数计算公式：

根据公式(3)可得，，结合Sigmoid激活函数的导数性质及均分误差计算函数，可以得到，

将(5)式代入公式(1)，可以得到权重的更新值为：

        这样，我们就得到了第二次MLP中的权重参数更新值。模型中剩余待确定的参数为第二层阈值、第一次权重、第一次阈值。类似地我们可以推导出第二层的阈值参数更新：

        采用和第二层权重更新同样的方法，来推导第一层权重：

同理可以得到第一层阈值参数更新为。

        为了方便进一步计算，我们定义梯度项:

        综上，我们可以得到双层感知机中所有模型参数的更新值如下：

由此，我们可以得出双层感知机模型的参数更新算法：

'''
伪代码
输入：训练集D={(Xk,Yk)} 1<=k<=|D|
     学习率
输出：更新权重后的前馈网络
'''
while True:
    for k in range(|D|):
        Y*=model(Xk)#计算模型输出值Y*
        gj=compute_1() #计算第二层梯度项gj
        et=compute_2() #计算第一次梯度项et
        utj, vit, thetaj, gammat = update() #更新第二层权重、第一层权重、第二层阈值、第一次阈值
    if stop:#达到停止条件
        break

    

（三）、BP算法相关知识

        1. 累计BP算法。BP算法的目标是最小化训练集上的累计误差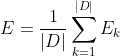。我们上边的参数更新推导是基于单个数据进行更新而推导的。基于单个数据推导出的更新算法称为“标准BP算法”，每处理一个数据即进行一次参数更新；根据累积误差推导出的更新算法称为“累计BP算法”。“累计BP算法”在处理所有数据后再进行参数更新，在训练数据集较大时效率更高。

        2. 过拟合。Horinik等人在1989年证明，一个包含足够多的神经元的隐藏层，多层前馈网络就能够以任意精度逼近任意复杂度的联系函数。由于前馈网络的表达能力强大，BP网络很容易出现过拟合。两种常用的处理过拟合方式一是“早停”（Early Stop），二是增加“正则化项”。

        3. 局部极小与全局最小。不同参数组合构成不同的前馈网络，寻找最优参数的过程可以理解为在寻找使误差最小的高维空间“点”。仅依靠梯度进行搜索，很容易使得参数陷入“局部极小”值，而我们的目标是尽可能的找到“全局最小”值。为了避免陷入“局部极小”值，最常用的方式为“随机梯度下降”法。在计算梯度时加入随机项，使得局部极小也有可能跳出继续搜索。

        4. 深度学习（Deep Learning）。随着计算机计算能力的提高，特别是GPU的高并行能力增加，层数更深、参数更多、结构更复杂的神经网络模型开始大规模的出现，其高性能使得其一直的研究及应用的热门方向。深度学习模型我们将在后面详细介绍。