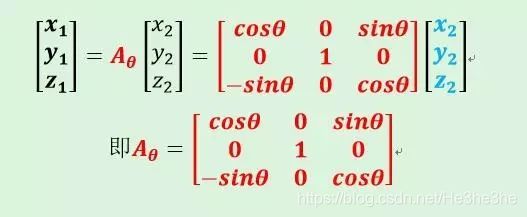【一】欧式空间、欧式变换
1.基
首先,基的数学定义如下:
先来看看线性相关:一个向量组里,只要有一个向量可以由其它向量线性表示,我们就称这个向量组线性相关。比如:
- {a1, a2, a3} 线性相关,因为 a1+a3 = a2;
- {a4, a5},{a4, a7}都线性相关
那么,线性无关:如果向量组里的任意一个向量都不能由其它向量线性表示,大家都是独一无二的存在。比如在二维平面上{a1, a3}线性无关,因为不共线
为了方便计算或者表示空间中的向量,我们一般选择正交基(例如:直角坐标系)
2.欧拉角:
欧拉角有三种:
- 俯仰:Pitch(绕y轴旋转)
- 偏航:Yaw(绕z轴旋转)
- 翻滚:Roll(绕x轴旋转)
常用的一种:偏航-俯仰-翻滚(yaw-pitch-roll)等价于ZYX轴旋转,向量表示为[r, p, y]
欧拉角的一个重大缺陷是会碰到万向锁问题:在俯仰角为±90度时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失一个自由度。(万向锁问题)
3.旋转的表示方式:
- 旋转矩阵:绕坐标轴依次旋转
- 旋转向量:绕任意轴一次直接旋转一个角度得到
3.1.旋转矩阵
首先,旋转矩阵是一个3×3的正交矩阵,即R^TR=E,但是9个未知数,只有6个约束(对角约束相同),所以有3个自由度,当然可以类推,m阶矩阵共有m(m-1)/2个自由变量 。
我们先绕某一个轴进行旋转,例如:x轴,那么分为两种情况:顺时针旋转和逆时针旋转,我们采用高中还是初中学的力的分解来求解旋转矩阵,将y轴和z轴视为一种力,然后将其正交分解在新的坐标轴y'和z' ,然后再进行力的合成可以得到如下的结果:
- 逆时针旋转 (旋转前:z,y,旋转后:z',y')
- 顺时针旋转(旋转前:z',y',旋转后:z,y)
3.2.姿态求解
- 旋转z轴:旋转前坐标:(x0, y0, z0), 旋转后坐标:(x1, y1, z1)
- 旋转y轴:旋转前坐标:(x1, y1, z1), 旋转后坐标:(x2, y2, z2)
- 旋转x轴:旋转前坐标:(x2, y2, z2), 旋转后坐标:(x3, y3, z3)
4.旋转向量
旋转矩阵表示的局限性:
- SO(3)旋转矩阵有9个量,但自由度为3,因此表示方法有冗余,同理可得,变换矩阵16个量,但是自由度为6。
- 旋转矩阵带有约束,它必须为正交矩阵,且行列式为1,优化时困难。
在三维中,旋转可以通过单一的旋转角 θ和所围绕的单位向量方向 v=(x,y,z)来定义。对于旋转向量r,其方向与旋转轴一致,长度等于旋转角θ
旋转向量到旋转矩阵:
旋转矩阵到旋转向量:
#include
#include
#include
#include
// 1. Eigen 实现
// 旋转向量转旋转矩阵
Eigen::Vector3d rvec (r_x, r_y, r_z);
double n_norm = rvec.norm();
Eigen::AngleAxisd rotation_vector (n_norm, rvec/n_norm);
Eigen::Matrix3d rotm;
rotm = rotation_vector.toRotationMatrix();
// 旋转矩阵转旋转向量
Eigen::Matrix3d rotation_matrix;
rotation_matrix << x_00,x_01,x_02,x_10,x_11,x_12,x_20,x_21,x_22;
Eigen::AngleAxisd rotation_vector;
rotation_vector.fromRotationMatrix(rotation_matrix);
// 2. OpenCV 实现
// 旋转向量转旋转矩阵
cv::Mat rvec = (cv::Mat_(3,1) << r_x, r_y, r_z);
cv::Mat rotm;
cv::Rodrigues(rvec, rotm);
// 旋转矩阵转旋转向量
cv::Mat rvec;
cv::Mat rotm = (cv::Mat_(3,3) << x_00,x_01,x_02,x_10,x_11,x_12,x_20,x_21,x_22);
cv::Rodrigues(rotm, rvec); - 证明:罗德里格斯(Rodrigues)旋转方程推导
-
罗德里格斯公式 理解、推导
参考:
- 机器人学之3D欧式变换理论与实践
- 三维空间的刚体运动
- 旋转矩阵
- 三维坐标系旋转——旋转矩阵到旋转角之间的换算
- 三维旋转矩阵推导
- 旋转矩阵(Rotation Matrix)的推导及其应用