数据结构の学习记录（进阶篇1）：什么是二叉查找树

对算法类的问题，最大的忌讳就是，想都不想直接写代码。

如果你的这样的程序猿，那么狠抱歉，要么就是你会花上数十倍的时间修改你的简单STUPID错误，要么就是你很短时间就能得到正确的结果，如果是这样那么恭喜你，你进化了！

说上述言论，笔者的区分点是你的目标究竟是一个码农还是一个算法工程师。两者的区别从工资上看不说你应该也懂:-)

（等不及的你可以迅速下拉到分界线以下寻找干货）

下面附上笔者的coding习惯。首先将思路以母语（中文可以但推荐英语）的形式写在草稿纸上，觉得没有问题之后，再将其用铅笔转换为代码，之后将其写在你青睐的有调试功能的开发平台上（对于笔者是Spyder，PyCharm）。如果你发现的开发平台没有调试功能，那么你需要立刻更换！对于刚写好的代码，第一步永远是调试，而不是直接运行。最后一步是不断优化，考虑所有的情况，并且优化时间复杂度和空间复杂度，永远不是喊着“哈利路亚”，然后发邮件告诉你老板任务完成了。

                                                                              第一步：将算法写在草稿纸上 

                                                                            第二步：将其转换为铅字版 代码

 

                                                               第三步：转化为实际的代码，这一步基本上是调试

---

不幸的是，笔者的博客将不会有完整代码（示范代码除外），所有代码均已上传到码云上。如果时间和精力允许的话，强烈建议你根据思路，手动写一遍，相信你会感觉到全身毛孔舒张而不是想砸电脑的快感。

本文学习的前提是假设你已经初步了解了二叉树，并能灵活的使用它。如果你还不是很了解的话，欢迎查看我的博客相关教程。

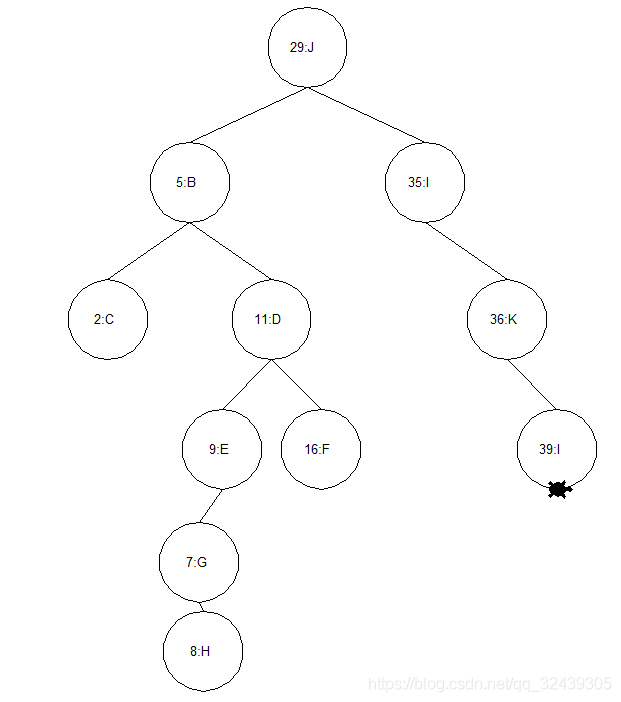
和hash表一样，二叉查找树设计的初衷是在尽可能小的时间复杂度下小完成查找过程，尤其是令人惊艳的log(n)，说实话，笔者在学习过程中就被惊讶到了。首先我们简单定义二叉查找树（Binary Search Tree，BST）。

所谓BST，就是把原来树的val变为 一个键（val）和一个负载（payload）：

class BSTNode:
    def __init__(self,val,payload,left=None,right=None,parent=None):
        self.val = val
        self.payload = payload
        self.left_child = left
        self.right_child = right
        self.parent = parent

我们在BST节点类里，加入一些很实用的功能。

（1）判断当前节点是左子节点还是右子节点isLeftChild，isRightChild。

（2）判断是否为根节点，也就是node.parent == None:

（3）判断是否为叶子节点isLeaf（左右子节点均为空）；

（4）判断至少有一个孩子 ；

（5）判断有两个孩子；

（6）删除叶节点；

 不得不说的是删除叶节点的操作非常需要注意。很多初学者是这样写的 Node = None。

这种写法具有很大问题。如果该节点是左子节点，需要考虑其父节点的左子节点，也就是设置node.parent.left_child = None。右子节点同理。

（7）设置一个节点的val和payload，左孩子和右孩子；

（8）节点迭代；

你可能会问，神马是节点迭代。比如说 for i in range(10)，类似地，我们想实现for node in BSTree: 其实这里的range就是一个迭代器。由于python是一个面向对象的语言，我们只需要在BSTNode里面实现__iter__()内置函数。同时你需要了解函数yield: 推荐博客https://blog.csdn.net/poyue8754/article/details/84680609 说白yield返回的不是一个值而是一个迭代器。如果我们要对1000个数进行迭代，使用for i in range(1000)太占用内存了，我们应该使用for i in xrange(1000):

节点遍历我们采用中序遍历的方式，也就是先遍历左孩子，再遍历根节点，再遍历右子树，都采用yield。所以代码应该为：

def __iter__(self):
        #implement the iteration mechanism utilising inorder transverse
        if self:
            if self.left_child!=None:
                for item in self.left_child:
                    yield item
            yield self
            if self.right_child!=None:
                for item in self.right_child:
                    yield item

你大概已经等不及了，好了让我们正式介绍二叉查找树把！而值得注意的是，这也是AVL树和红黑树的学习基础（惊喜：我后续博客会详细讲解它们）！我们希望在树中两种重要的操作——插入和删除的时间复杂度都是log(n)。

首先让我们来实现一些有趣的内部方法：

（1）__setitem__()：当我们在类中实现这个函数，就能像数组一样用下标进行赋值。

（2）__getitem__()：当我们在类中实现这个函数，就能像数组一样用下标进行访问。

（3）__contains__()：允许我们像 if i in Tree一样去查询某个val是否存在。

（4）__delitem__()：允许我们像del Tree[val]一样去删除某个节点。

（5）__iter__()：树的迭代，直接对根节点调用__iter__()

我们先考虑如何添加一个值val到树中。如果你能拿出笔和纸，记录的话，那是再好不过的了。

首先如果树为空，那么根节点的值设为val。

否则，我们需要按照一定的规则，当前节点从根节点开始，其值currVal和val进行比较：

1. 如果currVal>val: 创建一个左子节点，将当前节点变为左子节点，继续比较；

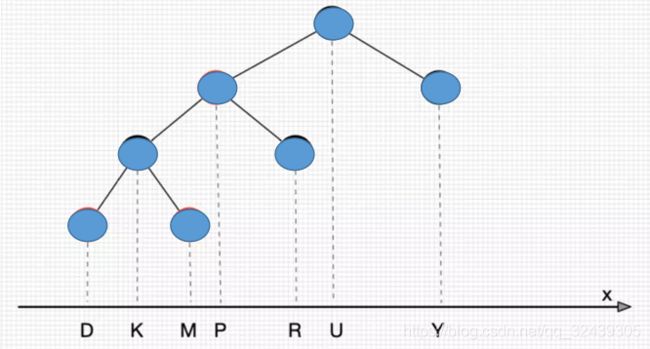
2.如果currVal

3.如果currVal==val: 我们修改当前节点的payload为插入的payload。

可以借助上述图片进行理解（左子树<根节点<右子树）。请注意，插入操作也是一个递归的过程。

我们现在来考虑删除一个节点的操作，它有三种情况：

（1）叶子节点

叶子节点的删除是非常简单的。首先用isLeaf() 判断其为叶子节点，之后我们直接删除即可。

（2）一个子节点

其次是一个子节点的情况，我们只需要将左（右）孩子，替换父亲即可（有点大义灭亲的感觉哈哈:-^o）。

node.left_child.parent = node.parent
node.parent.left_child = node .left_child 

（4）两个子节点 

这种情况最为复杂。还好我们有很优秀的插画师帮我们理解：

我们把节点投影到数轴上，以P为例，和它相邻最近的右节点R，称为后继。和它相邻最近的左节点M，称为前驱。我们要做的就是找到删除节点的后继节点或者前驱节点替换它，以保持BST性质，实际上相当于删除的是替换节点！

我们需要写一个函数find_successor来寻找我们的后继。这该如何操作呢？

你可以自己画几棵树，寻找规律：。。。。（仔细作图中）

---

很棒，你已经发现：后继节点是当前节点的右子树的最左子节点。我们可以用一个递归来实现，遍历右子树，直到左子树为空为止。找到后继节点后，再像前三种情况一样删除后继节点即可，查找到的节点的val和payload用后继节点代替即可。

你可能问，我如果要删除根节点怎么办？Nice Question. 实际上，根节点并没有被删除，它只是被替换了，除非树没有右子树，这时候需要把根节点变为相应的左子节点。

很棒，你认真阅读完了上述内容，并且有了自己的理解，下一期，我们正式介绍AVL树！

希望本文对你有帮助！