LeetCode_4_树----恢复二叉搜索树

大家好!我是你们的好朋友，大数据老虾。相遇是缘，既然来了就拎着小板凳坐下来一起唠会儿，如果在文中有所收获，请别忘了一键三连，你的鼓励，是我创作的动力，废话不多说，直接**开干 吧。

先别急着走，文末干货，记得拎着小板凳离开的时候也给它顺走

恢复二叉搜索树

题目

解析：

给出一个二叉搜索树的根节点root，该树中恰好两个节点的值被错误的交换。

示例1：

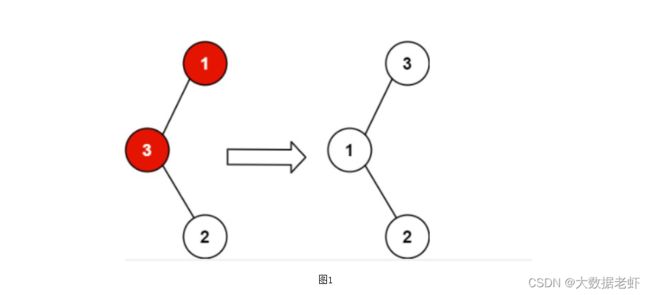
input：root = [1, 3, null, null, 2]
output：[3, 1, null, null, 2]
// 3 不能为1的左孩子，因为 3 > 1。交换 1 和 3 使二叉搜索树恢复有效

示例2：

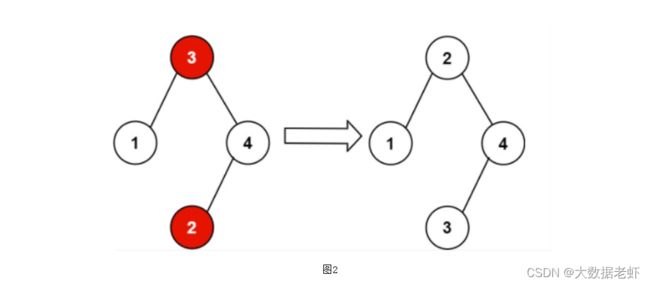
input：root = [3, 1, 4, null, null, 2]
output：[2, 1, 4, null, null, 3]
// 2 不能在 3 的右子树中，因为 2 < 3。交换 2 和 3 使二叉搜索树恢复有效。

方式1：显式中序遍历

思考：

如果两个节点被错误地交换后，会对原有的二叉树造成什么样地影响？

回答：

对于二叉搜索树而言，如果对其进行中序遍历，得到的值序列是递增有序的，而如果错误地交换了两个节点，等价于在这个值序列中交换了两个值，破坏了值序列的递增性。

假设有一个递增序列 a=[1,2,3,4,5,6,7]：

如果交换两个不相邻的数字，例如 22 和 66，原序列变成了a=[1,6,3,4,5,2,7]，那么显然序列中有两个位置不满足 ai < ai+1，在这个序列中体现为 6>3，5>2，因此只要找到这两个位置，即可找到被错误交换的两个节点。如果交换两个相邻的数字，例如 22 和 33，此时交换后的序列只有一个位置不满足ai

题解：

开辟一个新数组nums 来记录中序遍历得到的值序列，然后线性遍历找到两个位置 i 和 j，并重新遍历原二叉搜索树修改对应节点的值完成修复。

Java解题代码

class Solution {
    public void recoverTree(TreeNode root) {
        List<Integer> nums = new ArrayList<Integer>();
        inorder(root, nums);
        int[] swapped = findTwoSwapped(nums);
        recover(root, 2, swapped[0], swapped[1]);
    }

    public void inorder(TreeNode root, List<Integer> nums) {
        if (root == null) {
            return;
        }
        
        inorder(root.left, nums);
        nums.add(root.val);
        inorder(root.right, nums);
    }

    public int[] findTwoSwapped(List<Integer> nums) {
        int n = nums.size();
        int index1 = -1, index2 = -1;
        
        for (int i = 0; i < n - 1; ++i) {
            if (nums.get(i + 1) < nums.get(i)) {
                index2 = i + 1;
                if (index1 == -1) {
                    index1 = i;
                } else {
                    break;
                }
            }
        }
        
        int x = nums.get(index1), y = nums.get(index2);
        return new int[]{x, y};
    }

    public void recover(TreeNode root, int count, int x, int y) {
        if (root != null) {
            if (root.val == x || root.val == y) {
                root.val = root.val == x ? y : x;
                if (--count == 0) {
                    return;
                }
            }
            
            recover(root.right, count, x, y);
            recover(root.left, count, x, y);
        }
    }
}

复杂度分析

• 时间复杂度：O(N)O(N)，其中 NN 为二叉搜索树的节点数。中序遍历需要 O(N)O(N) 的时间，判断两个交换节点在最好的情况是 O(1)O(1)，最坏的情况下是O(N)O(N)，因此总时间复杂度为 O(N)O(N)。
• 空间复杂度：O(N)O(N)。需要用 nums 数组存储树的中序遍历列表。

文末彩蛋

找资料很累吧，别急客官，俺统统安排上。程序员不可缺少的书籍，程序员经典名言："收藏了就等于学会啦"
图灵程序丛书300+
Linux实战100讲
Linux书籍
计算机基础硬核总结
计算机基础相关书籍
操作系统硬核总结
Java自学宝典
Java学习资料
Java硬核资料
Java面试必备
Java面试深度剖析
阿里巴巴Java开发手册
MySQL入门资料
MySQL进阶资料
深入浅出的SQL
Go语言书籍
我的个人仓库：私人仓库