Java 笔试强训 牛客网选择编程题 02
一、选择
单选
将N条长度均为M的有序链表进行合并,合并以后的链表也保持有序,时间复杂度为()?
- A O(N * M * logN)
- B O(N*M)
- C O(N)
- D O(M)
1、建立一个长度为 N 的最大 / 最小堆。将这 N 条链表的第一个元素拿出来建立最小堆,时间复杂度:O(N)
2、依次从最小堆中取出元素(堆顶),此时堆顶就是当前集合的最小值,将链表的其他元素放入堆中。调整堆的时间复杂度:O(siftDown - N*M*logN),总共还需要入堆的元素个数,O(N*M*logN)
3、总共:建堆 + 不断调整堆(不断取出堆顶元素) O(N) + O(N*M*logN),取最高阶:O(N*M*logN)
大小为MAX的循环队列中,f为当前对头元素位置,r为当前队尾元素位置(最后一个元素的位置),则任意时刻,队列中的元素个数为
- A r-f
- B (r-f+MAX+1)%MAX
- C r-f+1
- D (r-f+MAX)%MAX
HASH 函数冲突处理方式不包括以下哪一项:
- A 开放定址法
- B 链地址法
- C 插入排序法
- D 公共溢出区法
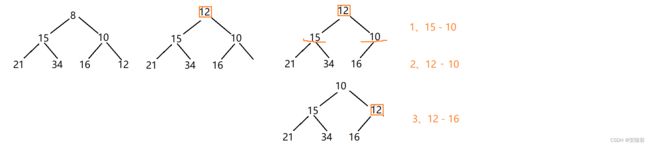
已知小根堆为8,15,10,21,34,16,12,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是() 。
- A 1
- B 2
- C 3
- D 4
堆顶和堆的最后一个元素交换,向下调整为小根堆
下列选项中,不可能是快速排序第2趟排序结果的是 ()
- A 2,3,5,4,6,7,9
- B 2,7,5,6,4,3,9
- C 3,2,5,4,7,6,9
- D 4,2,3,5,7,6,9
每进行一次快排,标定点一定处在最终位置。进行了两次快排,至少有两个元素到达最终位置:
A:2 3 9。B:2 9。C:9。D:5 9
堆排序平均执行的时间复杂度和需要附加的存储空间复杂度分别是()
- A O(N2)和O(1)
- B O(Nlog2N)和O(1)
- C O(Nlog2N)和O(N)
- D O(N2)和O(N)
原地堆排序
下面有关JVM内存,说法错误的是?
- A 程序计数器是一个比较小的内存区域,用于指示当前线程所执行的字节码执行到了第几行,是线程隔离的
- B Java方法执行内存模型,用于存储局部变量,操作数栈,动态链接,方法出口等信息,是线程隔离的
- C 方法区用于存储JVM加载的类信息、常量、静态变量、即时编译器编译后的代码等数据,是线程隔离的
- D 原则上讲,所有的对象都在堆区上分配内存,是线程之间共享的
方法区是线程共享的
下列程序段的输出结果是:( )
public void complicatedexpression_r(){ int x=20, y=30; boolean b; b = x > 50 && y > 60 || x > 50 && y < -60 || x < -50 && y > 60 || x < -50 && y < -60; System.out.println(b); }
- A true
- B false
- C 1
- D 0
输入流将数据从文件,标准输入或其他外部输入设备中加载道内存,在 java 中其对应于抽象类()及其子类。
- A java.io.InputStream
- B java.io.OutputStream
- C java.os.InputStream
- D java.os.OutputStream
下面关于程序编译说法正确的是()
- A java语言是编译型语言,会把java程序编译成二进制机器指令直接运行
- B java编译出来的目标文件与具体操作系统有关
- C java在运行时才进行翻译指令
- D java编译出来的目标文件,可以运行在任意jvm上
Java 是半编译半解释型语言
class 是与操作系统无关,面向 JVM 的二进制文件
1、编译:javac,*.java -> *.class。2、运行:java JVM 实际上此时会把 class 文件翻译成系统运行的机器码
JVM 也是有版本的,JDK11 的 class 文件 JDK8 是无法运行的
下面那些情况可以终止当前线程的运行?
- A 当一个优先级高的线程进入就绪状态时
- B 抛出一个异常时
- C 当该线程调用sleep()方法时
- D 当创建一个新线程时
线程的终止:
1、线程的任务执行完毕 (正常终止)
2、线程执行过程中出现异常 (异常终止)
public static void main(String args[]) {
Thread t=new Thread(){
public void run(){
dianping();
}
};
t.run();
System.out.print("dazhong"); }
static void dianping(){
System.out.print("dianping");
}
- A dazhongdianping
- B dianpingdazhong
- C a和b都有可能
- D dianping循环输出,dazhong夹杂在中间
本题中,线程 t 并没有启动,只是调用了run()方法,直接调用run(),没有启动新的线程,相当于调用普通方法而已。程序中运行的线程依然只有一个,那么程序会按照顺序执行,即先运行run(),run()方法调用dianping()方法输 出"dianping",程序继续向下执行输出"dazhong"。如果本题中t线程调用start()方法,就会出现C选项的情况。综上所述,正确答案为B。
public interface IService {String NAME=“default”;}
默认类型等价表示是哪一项:
- A public String NAME=“default”;
- B public static String NAME=“default”;
- C public static final String NAME=“default”;
- D private String NAME=“default”;
接口中的变量都是全局常量 public static final
有以下类定义:
abstract class Animal{ abstract void say(); } public class Cat extends Animal{ public Cat(){ System.out.printf("I am a cat"); } public static void main(String[] args) { Cat cat=new Cat(); } }运行后:
- A I am a cat
- B Animal能编译,Cat不能编译
- C Animal不能编译,Cat能编译
- D 编译能通过,但是没有输出结果
抽象类的子类必须覆写所有的抽象方法 (子类不是抽象类)
在Java中,以下关于方法重载和方法重写描述正确的是?
- A 方法重载和方法的重写实现的功能相同
- B 方法重载出现在父子关系中,方法重写是在同一类中
- C 方法重载的返回值类型必须一致,参数项必须不同
- D 方法重写的返回值类型必须相同或相容。
// 向上转型类的返回值可以
class A {
A test() {
return this;
}
}
class B extends A {
B test() {
return this;s
}
}
下列哪些语句关于内存回收的说明是正确的? ( )
- A 程序员必须创建一个线程来释放内存
- B 内存回收程序负责释放无用内存**
- C 内存回收程序允许程序员直接释放内存
- D 内存回收程序可以在指定的时间释放内存对象
JVM 垃圾回收由 JVM 来自己执行
下列语句正确的是:
- A 形式参数可被字段修饰符修饰
- B 形式参数不可以是对象
- C 形式参数为方法被调用时真正被传递的参数
- D 形式参数可被视为local variable
A:字段修饰符: 访问权限 public 等。C:实参。D:形式参数可被视为局部变量
在java7中,下列哪个说法是正确的:
- A ConcurrentHashMap使用synchronized关键字保证线程安全
- B HashMap实现了Collection接口
- C Arrays.asList方法返回java.util.ArrayList对象
- D SimpleDateFormat对象是线程不安全的
A:lock。B:Collection 接口是线性表的顶级接口,HashMap 实现 Map 接口。C:List 接口对象
public static <T> List<T> asList(T... a) {
return new ArrayList<>(a);
}
关于以下程序段,正确的说法是:()
String s1="abc"+"def";//1 String s2=new String(s1);//2 if(s1.equals(s2))//3 System.out.println(".equals succeeded");//4 if(s1==s2)//5 System.out.println("==succeeded");//6
- A 行4,行6都不执行
- B 行6执行,行4不执行
- C 行4执行,行6不执行
- D 行4,行6都将执行
字符串对象比较相等,使用 equals 比较内容,使用 == 比较就是地址
用命令方式运行以下代码的运行结果是()
public class f{ public static void main(String[] args){ String foo1 = args[1]; String foo2 = args[2]; String foo3 = args[3]; } }命令: java f a b c
- A 程序编译错误
- B a b c
- C 程序运行错误
- D f
编译命令:javac 源文件名称.java *.java -> *.class
运行命令:java 主类名称要传递的参数 (传递给main的args中)
java f a b c —— args{a, b, c} —— [0-2]
下列说法正确的是
- A 在类方法中可用this来调用本类的类方法
- B 在类方法中调用本类的类方法可直接调用
- C 在类方法中只能调用本类的类方法
- D 在类方法中绝对不能调用实例方法
A:this表示当前对象引用,不能调用静态域。B:静态方法没有对象可以直接使用。CD:如果在类方法中创建了对象,仍然可以通过对象来调用实例方法
class Test {
void func() {};
static void test() {
Test test = new Test();
test.func();
}
}
已知如下类说明:
public class Test{ private float f=1.0f; int m=12; static int n=1; public static void main(String args[]){ Test t=new Test(); } }如下哪些使用是正确的()
- A t.f = 1.0
- B this.n
- C Test.m
- D Test.n
有以下代码:
class A{ public A(String str){ } } public class Test{ public static void main(String[] args) { A classa=new A("he"); A classb=new A("he"); System.out.println(classa==classb); } }请问输出的结果是:
- A false
- B true
- C 报错
- D 以上选项都不正确
==比较的是两个引用的地址,classa和classb都是new出来的,地址必然不相等
以下哪项 不属于 java类加载过程?
- A 生成java.lang.Class对象
- B int类型对象成员变量赋予默认值
- C 执行static块代码
- D 类方法解析
B:成员变量不会被初始化,只有静态变量会被初始化。对象产生时执行,在类加载之后,不属于类加载过程
java中下面哪个能创建并启动线程()
public class MyRunnable implements Runnable { public void run() { //some code here } }
- A new Runnable(MyRunnable).start()
- B new Thread(MyRunnable).run()
- C new Thread(new MyRunnable()).start()
- D new MyRunnable().start()
创建并启动线程的过程为:定义线程->实例化线程->启动线程。 定义线程有两种方式,一种是继承java.lang.Thread类,一种是实现java.lang.Runnable接口。这两种方式实例化线程区别在于,如果是继承了Thread类,直接 new一个对象就可以了,如果是实现了Runnable接口的类,则需要用Thread的构造方法: Thread(Runnable target) Thread(Runnable target, String name) Thread(ThreadGroup group, Runnable target) Thread(ThreadGroup group, Runnable target, String name) Thread(ThreadGroup group, Runnable target, String name, long stackSize) 因此A、D两个选项实例化线程存在错误。B选项中new Runnable(MyRunnable)中的MyRunnable还没有实例化,会导致编译不通过,该选项无论后面是调用 run()还是start()都是错误的。
如果希望监听TCP端口9000,服务器端应该怎样创建socket?
- A new Socket(“localhost”,9000);
- B new ServerSocket(9000);
- C new Socket(9000);
服务器端使用 ServerSocket(int port),默认在本地指定端口号监听 TCP 端口
客户端使用Socket来连接服务器 Socket(lP,port)
下列哪个类的声明是正确的?
A abstract final class HI{}
B abstract private move(){}
C protected private number;
D public abstract class Car{}
java 接口的修饰符可以为()
- A private
- B protected
- C final
- D abstract
题目指直接在接口定义上使用的修饰符,接口权限都是 public
jre 判断程序是否执行结束的标准是()
- A 所有的前台线程执行完毕
- B 所有的后台线程执行完毕
- C 所有的线程执行完毕
- D 和以上都无关
JRE:Java 运行时环境
JDK:Java开发工具包,包含了 JRE
什么时候 Java 进程认为程序全部执行完毕:所有前台线程(用户线程)执行完毕
手动置为后台线程:setDameon(true)
一般我们创建的线程都是前台线程。后台线程:JVM垃圾回收线程
int i=5;
int s=(i++)+(++i)+(i–)+(–i);
s=( )//s 的值是什么?
- A 28
- B 25
- C 21
- D 26
- E 24
- F 23
5 7 7 5
下面不属于Object类中方法的是:
- A hashCode()
- B finally()
- C wait()
- D toString()
finalize() 是 Object 类的方法,用于释放线程资源
下列哪项不属于jdk1.6垃圾收集器?
- A Serial收集器
- B parNew收集器
- C CMS收集器
- D G1收集器
JDK7之后版本
instanceof运算符能够用来判断一个对象是否为:
- A 一个类的实例
- B 一个实现指定接口的类的实例
- C 全部正确
- D 一个子类的实例
以下哪项是类实例化的语句?
- A varName ClassName=new varName();
- B ClassName varName=new ClassName(new ClassName);
- C ClassName varName=ClassName();
- D ClassName varName=new ClassName();
类名称 引用名称 = new类();
当你编译和运行下面的代码时,会出现下面选项中的哪种情况?
public class Pvf{ static boolean Paddy; public static void main(String args[]){ System.out.println(Paddy); } }
- A 编译时错误
- B 编译通过并输出结果false
- C 编译通过并输出结果true
- D 编译通过并输出结果null
类中声明的变量有默认初始值;方法中声明的变量没有默认初始值,必须在定义时初始化,否则在访问该变量时会出错。 本题中Paddy是静态的成员变量,因此它会获得boolean类型的初始值false。
以下叙述正确的是
- A 实例方法可直接调用超类的实例方法
- B 实例方法可直接调用超类的类方法
- C 实例方法可直接调用子类的实例方法
- D 实例方法可直接调用本类的实例方法
A:super()。B:类名称。C:子类对象
HashSet子类依靠()方法区分重复元素。
- A toString(),equals()
- B clone(),equals()
- C hashCode(),equals()
- D getClass(),clone()
先调用对象hashcode方法将对象映射为数组下标,再通过equlas来判断元素内容是否相同
以下代码在编译和运行过程中会出现什么情况
public class TestDemo{ private int count; public static void main(String[] args) { TestDemo test=new TestDemo(88); System.out.println(test.count); } TestDemo(int a) { count=a; } }
- A 编译运行通过,输出结果是88
- B 编译时错误,count变量定义的是私有变量
- C 编译时错误,System.out.println方法被调用时test没有被初始化
- D 编译和执行时没有输出结果
private在类内部可以使用,count是成员变量,通过对象访问
以下程序执行的结果是:
class X{ Y y=new Y(); public X(){ System.out.print("X"); } } class Y{ public Y(){ System.out.print("Y"); } } public class Z extends X{ Y y=new Y(); public Z(){ System.out.print("Z"); } public static void main(String[] args) { new Z(); } }
- A ZYXX
- B ZYXY
- C YXYZ
- D XYZX
初始化父类中的静态成员变量和静态代码块 ; 初始化子类中的静态成员变量和静态代码块 ; 3.初始化父类的普通成员变量和代码块,再执行父类的构造方法; 4.初始化子类的普通成员变量和代码块,再执行子类的构造方法; 具体过程如下“ (1)初始化父类的普通成员变量和代码块,执行 Y y=new Y(); 输出Y (2)再执行父类的构造方法;输出X (3)初始化子类的普通成员变量和代码块,执行 Y y=new Y(); 输出Y (4)再执行子类的构造方法;输出Z 所以选C
- 继承时先调用父类的构造方法
- 类中成员变量的初始化操作都在构造方法中进行
有这么一段程序:
public class Test{ public String name="abc"; public static void main(String[] args){ Test test=new Test(); Test testB=new Test(); System.out.println(test.equals(testB)+","+test.name.equals(testB.name)); } }请问以上程序执行的结果是()
- A true,true
- B true,false
- C false,true
- D false,false
Object提供的equals方法,默认是比较对象地址是否相同。而字符串重写了 equals 方法,比较的是值是否相等。
考虑下面这个简单的例子,让我们看看reflection是如何工作的。
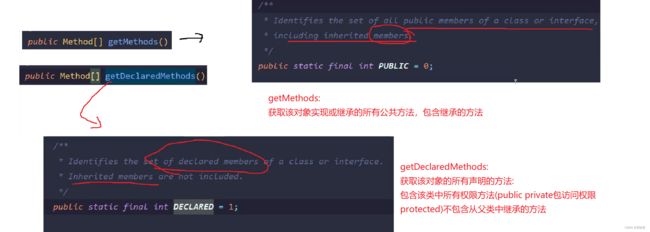
import java.lang.reflect.*; public class DumpMethods{ public static void main(String[] args) { try { Class c=Class.forName(args[0]); Method m[]=c.getDeclaredMethods(); for (int i = 0; i < m.length; i++) { System.out.println(m[i].toString()); } } catch (Throwable e) { System.err.println(e); } } }其中"c.getDeclaredMethods"的作用是:
- A 取得类的公有方法对象
- B 取得类的所有公有方法名称
- C 取得类的所有方法对象
- D 以上选项都不正确
java 的字符类型采用的是 Unicode 编码方案,每个 Unicode 码占用()个比特位。
A 8
B 16
C 32
D 64
以下多线程对int型变量x的操作,哪个不需要进行同步()
A ++x
B x=y
C x++
D x=1
B:x的赋值依赖于一个变量非原子。D:直接的赋值操作属于原子操作
有如下4条语句:()
Integer i01=59; // 自动装箱 int i02=59; Integer i03=Integer.valueOf(59); // 装箱 Integer i04=new Integer(59); // 在堆上 new 了一个新对象以下输出结果为false的是:
A System.out.println(i01==i02); // 将i01自动拆箱,还原为整型
B System.out.println(i01==i03); // true
C System.out.println(i03==i04); // 有new就有新空间,i03和i04地址不等
D System.out.println(i02==i04); // 自动拆箱,i04还原为int
A、D选项,当包装类与基本数据类型对比时,包装类会自动拆箱变为基本类型再进行比较,即Integer i01会拆箱为int类型与i02对比。因 此System.out.println(i01==i02);输出为true。 B选项,包装数据类直接赋值,默认调用其对用的valueOf()方法。那么Integer i03=Integer.valueOf(59);就等价于Integer i01=59;valueOf()操作-128 ~ 127 之内的整型,在第一次引用,会在缓存中new一个对象;再次引用,直接从缓存中查找;操作-128 ~ 127之外的整型,则每次都要new一个对象。也就是说如果 已经创建了一个-128 ~ 127之间的整数,使用valueOf创建第二次时,不会使用new关键字,而用已经缓存的对象。因此System.out.println(i01==i03);输出 true。 C选项,包装类是基础数据类型的引用类型,i04的定义使用了new关键字,这会开辟出一块新内存来放置值为59的Integer对象。那么两个地址不同的引用类 型变量进行==判断结果自然是false。答案选择C。
// 原码:
public static Integer valueOf(int i) {
if (i >= IntegerCache.low && i <= IntegerCache.high)
return IntegerCache.cache[i + (-IntegerCache.low)];
return new Integer(i);
}
在单处理器系统中,如果同时存在有12个进程,则处于就绪队列中的进程数量最多为()
A 1
B 9
C 10
D 11
以下关于多线程的叙述错误的是:
- A 线程同步的方法包括使用临界区,互斥量,信号量等
- B 两个线程同时对简单类型全局变量进行写操作也需要互斥
- C 实现可重入函数时,对自动变量也要用互斥量加以保护
- D 可重入函数不可以调用不可重入函数
临界区:通过对多线程的串行化来访问公共资源或一段代码,速度快,适合控制数据访问。(临界区可以认为是操作共享资源的一段代码)
互斥量:为协调共同对一个共享资源的单独访问而设计的。信号量:为控制一个具有有限数量用户资源而设计。|
事件:用来通知线程有一些事件已发生,从而启动后继任务的开始
可重入函数:
主要用于多任务环境中,一个可重入的函数简单来说就是可以被中断的函数,也就是说,可以在这个函数执行的任何时刻中断它,转入OS调度下去执行另外一段代码,而返回控制时不会出现什么错误;
不可重入的函数:
由于使用了一些系统资源,比如全局变量区,中断向量表等,所以它如果被中断的话,可能会出现问题,这类函数是不能运行在多任务环境下的。
自动变量:
局部作用域变量,定义的时候才被创建,函数返回时,系统回收空问;属于线程私有的
系统死锁的可能的原因是
- A 进程死循环
- B 资源循环等待
- C 程序内存访问越界
- D 进程释放资源
整数0x12345678,在采用bigendian中内存的排序序列是( )
- A 12 34 56 78
- B 78 56 34 12
- C 87 65 43 21
- D 21 43 65 87
bigendian 大端模式,littleenddian 小端模式
使用C语言将一个1G字节的字符数组从头到尾全部设置为字’A’,在一台典型的当代PC上,需要花费的CPU时间的数量级最接近()
- A 0.001秒
- B 1秒
- C 100秒
- D 2小时
单位之间的换算规则是:
1GB = 1024MB
1MB = 1024KB
1KB = 1024B
1B = 8bits
所以1GB = 1,073,741,824B
执行1条语句约 1ns即1/1,00o,000 ,000秒(10^9),每次赋值1B都要执行一次语句,所以对于1G来说大约是1秒 10^9 * 1,073,741,824
对于普通的计算机,对以下事件的平均耗时从小到大排序为____:
A.读取1KB内存数据 B.从硬盘连续读取1KB数据 C.读取一次L2缓存 D.一次磁盘寻道
- A C,A,D,B
- B C,D,A,B
- C D,C,A,B
- D D,A,C,B
缓存是level 2缓存是二级缓存的意思,通过缓存直接与cpu进行数据交互,这个是最快最直接的。
第二个内存读取时间,当通过CPU缓存寻找数据时发现数据在缓存中不存在这时需要通过,到内存中去寻找,但是内存的传输速度就没有缓存这么快了,所以,内存读取数据的时间消耗要大于缓存。
第三个从硬盘连续读取1kb,这个意思就是读取硬盘数据,其中读取硬盘数据的时间消耗主要由是寻道时间,数据传输时间,还有旋转时间三部分时间组成,所以其中的磁盘寻道时间肯定小于总的连续读取时间。
分页式虚拟存储管理系统中,页面的大小与可能产生的缺页中断次数( )
- A 成正比
- B 成反比
- C 无关
- D 成固定值
分页式虚拟存步系统:
将作业信息 (指内存要操作的数据信息) 的副本存放在磁盘这一类辅助存储器中,当作业被调度投入运行时,并不把作业的程序和数据全部装入主存,而仅仅装入立即使用的那些页面,至少要将作业的第一页信息装入主存,在执行过程中访问到不在主存的页面时,再把它们动态地装入。
用得较多的分页式虚拟存储管理是请页式 (demand Paging),当需要执行某条指令或使用某个数据,而发现它们并不在主存时,产生一个缺页中断,系统从辅存中把该指令或数据所在的页面调入内存。
进入内存的页面内容是没有变化的。所以分页式虚拟存储管理系统中,页面的大小与可能产生的缺页中断次数关系不大。
关于子进程和父进程的说法,下面哪一个是正确的?()
- A 一个父进程可以创建若干个子进程,一个子进程可以从属于若干个父进程
- B 父进程被撤销时,其所有子进程也被相应撤消
- C 子进程被撤销时,其从属的父进程也被撤销
- D 一个进程可以没有父进程或子进程
A:一个父进程可以创建多个子进程,但一个子进程只从属于1个父进程
B:如果父进程先退出,子进程还没退出,那么子进程将被托孤给 init进程,并由init进程对它们完成状态收集工作。这时子进程的父进程就是init进程((1号进程)。init进程没有父进程。
C:子进程退出,父进程还可以继续执行
D: init进程没有父进程;一个进程,可以不创建子进程
关于线程和进程,下面说法正确的是()
- A 终止一个进程比终止一个线程花费的时间少
- B 进程切换比同一进程内部的线程切换花费的时间少
- C 线程提高了不同执行程序间的通信效率
- D 进程和线程都是资源分配和调度的基本单位
进程的创建,切换,终止,耗时/消耗的资源都比线程要高。A B改成高,D 是进程
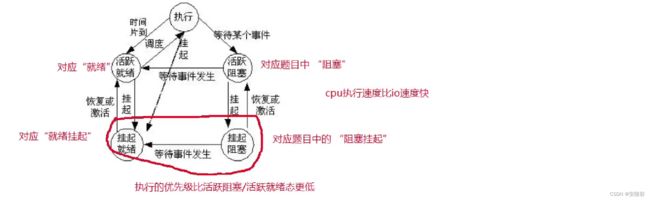
进程调度时,下列进程状态的变化过程哪一项是不可能发生的?()
- A 阻塞挂起->阻塞
- B 就绪挂起->就绪
- C 就绪挂起->阻塞挂起
- D 阻塞挂起->就绪挂起
处于运行状态的操作系统程序应放在()
- A 寄存器中
- B 主存中
- C 辅存中
运行状态的操作系统程序指的是进程,在主存中
寄存器:容量有限,只是加载 CPU 执行代码所需要的数据(从主存加载到寄存器)
辅存:进程挂起状态,进程就会保存在辅存中
在系统内存中设置磁盘缓冲区的主要目的是()。
- A 减少磁盘 I/O 次数
- B 减少平均寻道时间
- C 提高磁盘数据可靠性
- D 实现设备无关性
磁盘缓冲区有磁盘和磁盘缓冲区
cpu执行速度 比 磁盘io速度 要快很多
为了提高效率,经常访问的磁盘数据,可以使用磁盘缓存来:提高 io 速度
B 不是减少寻道时间,而是次数
下列选项中,会导致进程从执行态变为就绪态的事件是()。
- A 执行 P(wait)操作
- B 申请内存失败
- C 启动 I/O 设备
- D 被高优先级进程抢占
A:进程通信其中一种方式,信号: p (wait) 信号量 -1,v (signal)信号量 +1。要根据信号量,如果是正数,就可以继续执行
B:操作系统内核会通知进程,由进程自己决定如何执行,一般情况是报错
下面哪一种表述不属于操作系统的主要功能?()
- A 处理机管理
- B 存储器管理
- C 设备管理和文件管理
- D 可移植
处理机管理:进程管理
在现代操作系统中采用缓冲技术的主要目的是()。
- A 改善用户编程环境
- B 提高CPU的处理速度
- C 提高CPU和设备之间的并行程度
- D 实现与设备无关性
cpu 执行的速度比磁盘 io 的速度要快很多,所以在中间加了一个缓冲区。cpu同时可以对缓冲区读写数据,磁盘也可以对缓冲区读写数据
进程和程序的一个本质区别是()。
- A 前者为动态的,后者为静态的
- B 前者存储在内存,后者存储在外存
- C 前者在一个文件中,后者在多个文件中
- D 前者分时使用CPU,后者独占CPU
程序是外存中静态的可执行文件。进程如果是运行状态,就在内存中,如果是挂起状态,就在外存。D:程序没有运行起来,是静态的可执行文件,说法错误
一个进程的读磁区操作完成后,操作系统针对该进程必做的是 ()
- A 修改进程状态为就绪态
- B 降低进程优先级
- C .进程分配用户内存空间
- D 增加进程的时间片大小
进程io操作是阻塞,读了一段到缓冲区,通知操作系统调度该进程,从阻塞状态到就绪状态
BCD 与 io 操作无关
选择在最近的过去很久未访问的页面予以淘汰的算法称为()。
- A Opt.
- B LRU
- C MFU
- LFU
OPT (Optimal page replacement algorithm)
最佳页面替换算法,预测哪个页面最晚出现,就替换哪个页面。
LRU(Least Recently Used)
最近最少使用页面置换算法,也就是首先淘汰最长时问未被使用的页面。
MFU (Most Frequently Used)
最常使用算法,替换最常使用的页面
LFU ( Least Frequently Used)
最近最不常用页面置换算法,淘汰一定时期内被访问次数最少的页面。
并发进程之间()。
- A 彼此无关
- B 必须同步
- C 必须互斥
- D 可能需要同步或互斥
互斥:
是指散步在不同任务之问的若干程序片断,当某个任务运行其中一个程序片段时,其它征务就不能运行它们之中的任一程序片段,只能等到该任务运行完这个程序片段后才可以运行。最基本的场景就是∶一个公共资源同一时刻只能被一个进程或线程处用,多个进程或线程不能同时使用公共资源。
同步:
是指散步在不同任务之间的若干程序片断,它们的运行必须严格按照规定的某种先后次序来运行,这种先后次序依赖于要完成的特连的任务。最基本的场景就是:两个或两个以上的进程或线程池运行过程中协同步调,按预定的先后次序运行。比如A任务的运行依赖干B任务产牛的数据。
显然,同步是一种更为复杂的互斥,而互斥是一种特殊的同步。
一次I/O操作的结束,有可能导致()。
- A 一个进程由睡眠变就绪
- B 几个进程由睡眠变就绪
- C 一个进程由睡眠变运行
- D 几个进程由睡眠变运行
若一个用户进程通过read 系统调用读取一个磁盘文件中的数据,则下列关于此过程的叙述中,正确的是( )。 Ⅰ. 若该文件的数据不在内存中,则该进程进入睡眠等待状态 Ⅱ. 请求 read 系统调用会导致 CPU 从用户态切换到核心态 Ⅲ. read 系统调用的参数应包含文件的名称
- A 仅Ⅰ、 Ⅱ
- B 仅Ⅰ、 Ⅲ
- C 仅Ⅱ、 Ⅲ
- D Ⅰ、 Ⅱ和Ⅲ
read 是 io 读,1、磁盘读数据到内存,2、CPU 从内存获取数据 (快),
Ⅰ. 若文件的数据不在内存中,则讲程讲入睡眠模式的目的是等待内存对磁盘上文件的映射,因为磁盘的读取此较慢,所以事进入睡眠模式。
Ⅱ. read是系统调用,所以CPU从用户态切换到核心态。
Ⅲ. open系统调用应该包含文件的名称,read只是包含输入流。
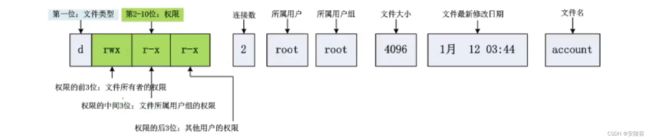
Linux文件权限一共10位长度,分成四段,第三段表示的内容是()?
- A 文件类型
- B 文件所有者的权限
- C 文件所有者所在组的权限
- D 其他用户的权限
关于读写锁的描述,以下正确的是()
- A 在任何时刻,获得锁权限的线程只有一个
- B 读写锁可以同时存在读者和写者
- C 读写锁在写加锁状态时,其他进行写操作线程不会阻塞,一直循环查询读写锁是否可用
- D 读写锁在读加锁的状态下,可用进行读共享
写锁加锁时,其他线程不能再进行读操作(申请加读谈),写操作(申请加写锁),也就是写写互斥,读写互斥
读锁加锁时,其他线程还能进行读操作,也就是读读并发
进程阻塞的原因不包括________。
- A 时间片切换
- B 等待I/O
- C 进程sleep
- D 等待解锁
解析:进程有3个状态:就绪态,执行态、阻塞态。三种状态的转换包含有: 就绪->执行,执行->就绪,执行->阻塞,阻塞->就绪,等待I/O、进程sleep、等待解锁等原因都会导致进程暂停。关于"时间片切换",当进程已经获得了除cpu外所有的资源,这时的状态就是就绪态,当分配到了时间片就成了执行态,当时间片用完之前一直未进入阻塞态的话,此后便继续进入就绪态。所以进程的就绪与阻塞是完全不同的。
在缺页处理过程中,操作系统执行的操作可能是()。 Ⅰ.修改页表 Ⅱ.磁盘 I/O Ⅲ.分配页框
- A 仅Ⅰ、 Ⅱ
- B 仅Ⅱ
- C 仅Ⅲ
- D Ⅰ、 Ⅱ和Ⅲ
缺页:
是引入了虚拟内存后的一个概念。操作系统启动后,在内存中维护着一个虚拟地址表,进程需要的虚拟地址在虚拟地址表中记录。一个程序被加载运行时,只是加载了很少的一部分到内存,另外一部分在需要时再从磁盘载入。
加载到内存的部分标识为“驻留",而未被加载到内存的部分标为"未驻留"。 操作系统根据需要读取虚拟地址表,如果读到虚拟地址表中记录的地址被标为"未驻留”,表示这部分地址记录的程序代码未被加载到内存,需要从磁盘读入,则这种情况就表示"缺页"。
页框:
CPU中添加了能自动把虚拟内存(即逻辑地址)地址转化为物理内存地址的电路,为了简化这种电路,就把RAM划分为长度为4KB或8KB的块,这种块就叫页框。
内核以页框为基本单位管理物理内存,分页单元中,页 指进程内存在虚拟内存中这样的一组数据,而存放这组数据的物理内存就是页框,当这组数据被释放后,若有其他进程请求访问此内存,那么页框中的页将会改变。
二、编程题
年终奖 —— 动态规划
小东所在公司要发年终奖,而小东恰好获得了最高福利,他要在公司年会上参与一个抽奖游戏,游戏在一个6*6的棋盘上进行,上面放着36个价值不等的礼物,每个小的棋盘上面放置着一个礼物,他需要从左上角开始游戏,每次只能向下或者向右移动一步,到达右下角停止,一路上的格子里的礼物小东都能拿到,请设计一个算法使小东拿到价值最高的礼物。
给定一个6*6的矩阵board,其中每个元素为对应格子的礼物价值,左上角为[0,0],请返回能获得的最大价值,保证每个礼物价值大于100小于1000。
import java.util.*;
public class Bonus {
public int getMost(int[][] board) {
// write code here
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (i == 0 && j == 0) {
continue;
} else if (i == 0) { // 上面没有 最大值就是 加上前一个
board[i][j] += board[i][j - 1];
} else if (j == 0) { // 左边没有 最大值就是 加上上一个
board[i][j] += board[i - 1][j];
} else { // 加左一个和上一个的最大值
board[i][j] += Math.max(board[i][j - 1], board[i - 1][j]);
}
}
}
// 返回最后一个
return board[board.length - 1][board[0].length - 1];
}
}
迷宫问题 —— 递归
定义一个二维数组 N*M ,如 5 × 5 数组下所示:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的路线。入口点为[0,0],既第一格是可以走的路。
数据范围: 2≤n,m≤10, 输入的内容只包含 0≤val≤1
输入描述:
输入两个整数,分别表示二维数组的行数,列数。再输入相应的数组,其中的1表示墙壁,0表示可以走的路。数据保证有唯一解,不考虑有多解的情况,即迷宫只有一条通道。
输出描述:
左上角到右下角的最短路径,格式如样例所示。
输入
5 5
0 1 0 0 0
0 1 1 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出
(0,0)
(1,0)
(2,0)
(2,1)
(2,2)
(2,3)
(2,4)
(3,4)
(4,4)
【解题思路】
每一个位置有四个方向:
可以走的方向:没有越界,没有障碍,之前没有走过
搜索:
当前位置 (x, y):
判断:(x, y) 是否越界,(x, y)之前是否走过,(x, y)是否有障碍
没有越界,没有走过,没有障碍:
- 把当前位置保存在到路径中
- (x, y) 是右下角,出口位置:一条新的路径产生
判断新的路径是否为更短路径,如果是更短路径,更新路径 - 继续搜素 (x, y) 四个方向
- 把当前位置从路径中删除,寻找新的路径
import java.util.*;
// 存放当前位置 (x, y)
class Node {
int x;
int y;
public Node(int x, int y) {
this.x = x;
this.y = y;
}
}
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 迷宫矩阵
int row = scanner.nextInt();
int col = scanner.nextInt();
int[][] maze = new int[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
maze[i][j] = scanner.nextInt();
}
}
// 搜索最短路径
ArrayList<Node> path = new ArrayList<>();
ArrayList<Node> minPath = new ArrayList<>();
int[][] book = new int[row][col];
getMinPath(maze, row, col ,0, 0, book, path, minPath);
// 打印最短路径
for (Node node : minPath) {
System.out.println("(" + node.x + "," + node.y + ")");
}
}
/**
* @param maze 迷宫矩阵
* @param row col 行 列
* @param x y 当前位置
* @param book 标记当前矩阵,标记当前位置是否走过
* @param path 保存当前路径的每一个位置
* @param minPath 记录最短路径
*/
private static void getMinPath(int[][] maze, int row, int col, int x, int y, int[][] book, ArrayList<Node> path, ArrayList<Node> minPath) {
// 1、判断 (x, y) 是否越界、走过、有障碍
if (x < 0 || x >= row || y < 0 || y >= col
|| book[x][y] == 1 || maze[x][y] == 1) {
return;
}
// 2、把当前位置 存入路径
path.add(new Node(x, y));
// 3、标记当前为位置
book[x][y] = 1;
// 4、判断当前位置是否为出口
if (x == row - 1 && y == col - 1) {
// 到出口,一条新的路径产生,判断是否要更新最短路径
if (minPath.isEmpty() || path.size() < minPath.size()) {
minPath.clear();
for (Node node : path) {
minPath.add(node);
}
}
}
// 5、继续搜索以 (x, y) 的上下左右四个方向
getMinPath(maze, row, col, x - 1, y, book, path, minPath);
getMinPath(maze, row, col, x + 1, y, book, path, minPath);
getMinPath(maze, row, col, x, y - 1, book, path, minPath);
getMinPath(maze, row, col, x, y + 1, book, path, minPath);
// 6、回退到当前位置,把当前位置,从路径中删除,寻找新的路径
path.remove(path.size() - 1);
book[x][y] = 0;
}
}
数根
数根可以通过把一个数的各个位上的数字加起来得到。如果得到的数是一位数,那么这个数就是数根;如果结果是两位数或者包括更多位的数字,那么再把这些数字加起来。如此进行下去,直到得到是一位数为止。
比如,对于24 来说,把2 和4 相加得到6,由于6 是一位数,因此6 是24 的数根。
再比如39,把3 和9 加起来得到12,由于12 不是一位数,因此还得把1 和2 加起来,最后得到3,这是一个一位数,因此3 是39 的数根。
现在给你一个正整数,输出它的数根。
输入描述:
输入包含多组数据。
每组数据数据包含一个正整数n(1≤n≤10E1000)。
输出描述:
对应每一组数据,输出该正整数的数根。
输入
24
39
输出
6
3
【解题思路】
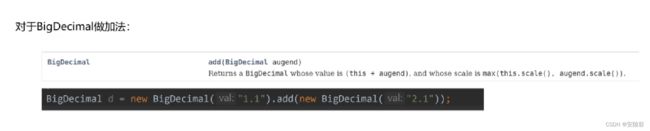
求正整数n的树根,n的范围为[1,10^1000 ]
int和long 都不在取值范围内,此时要接收输入的数据,只能考虑以下类型:
(1) BigDecimal
(2) String
题目要求是每一位来相加,相对来说,使用String从0开始遍历以后相加更加容易
要注意的事项:
(1)相加后的结果可能还不是一位数,即还不满足树根的要求,需要再次相加
如759,则为7+5+9=21,不是一位数,还需要再次计算:2+1=3,则树根为3
(2)字符串可以使用charAt(int index)方法获取字符,字符可以直接转换为int
特殊的,当字符是数字0-9时,可以使用字符与字符相减操作,即可得到数字的差值
如’9’- '6,返回值即为9-6的结果3
所以字符‘0"-‘9,要取int值,使用字符-"0’即可
如字符’5’,要获取数字值5,使用"5-0’即可
// write your code here
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
String n = scanner.nextLine(); // next
while (n.length() > 1) { // 字符串 "10" --> len > 1 而不是 10
int sum = 0;
for (int i = 0; i < n.length(); i++) {
sum += n.charAt(i) - '0'; // 各位相加
}
n = String.valueOf(sum);
}
System.out.println(n);
}
}
}
星际密码
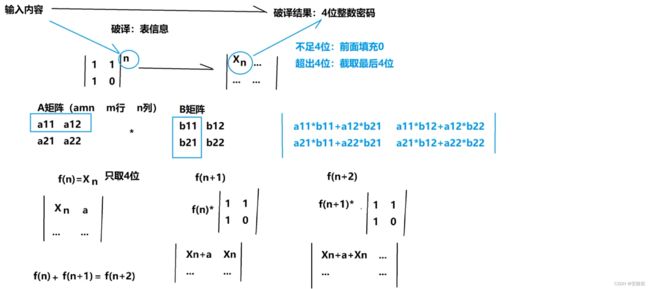
星际战争开展了100年之后,NowCoder终于破译了外星人的密码!他们的密码是一串整数,通过一张表里的信息映射成最终4位密码。表的规则是:n对应的值是矩阵X的n次方的左上角,如果这个数不足4位则用0填充,如果大于4位的则只输出最后4位。
|1 1|^n => |Xn …|
|1 0| |… …|
例如n=2时,
|1 1|^2 => |1 1| * |1 1| => |2 1|
|1 0| |1 0| |1 0| |1 1|
即2对应的数是“0002”。
输入描述:
输入有多组数据。
每组数据两行:第一行包含一个整数n (1≤n≤100);第二行包含n个正整数Xi (1≤Xi≤10000)
输出描述:
对应每一组输入,输出一行相应的密码。
输入
6
18 15 21 13 25 27
5
1 10 100 1000 10000
输出
418109877711037713937811
00010089410135017501
【解题思路】
提前准备 f(xi) 斐波那契的数据
接收多组测试用例
每组用例:
输入第一行:整数 n
第二行:n 个数值 xi
输出:每一个 xi 进行计算,f(xi),所有的结果拼接为字符串
import java.util.*;
public class Main {
public static void main(String[] args) {
// 准备斐波那契数列
int[] nums = new int[10001];
nums[1] = 1; // 从 1 开始,对应
nums[2] = 2;
for (int i = 3; i < 10001; i++) {
nums[i] = nums[i - 1] + nums[i - 2];
nums[i] = nums[i] % 10000; // 如果大于4位的则只输出最后4位
}
// 多组测试用例
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
StringBuilder stringBuilder = new StringBuilder();
int n = scanner.nextInt();
for (int i = 0; i < n; i++) {
int xi = scanner.nextInt();
// 拼接每个 xi 的密码 格式化输出 如果这个数不足4位则用0填充
stringBuilder.append(String.format("%04d", nums[xi]));
}
// 输出 n 个拼接的密码串
System.out.println(stringBuilder.toString());
}
}
}
快到碗里来
小喵们很喜欢把自己装进容器里的(例如碗),但是要是碗的周长比喵的身长还短,它们就进不去了。
现在告诉你它们的身长,和碗的半径,请判断一下能否到碗里去。
输入描述:
输入有多组数据。
每组数据包含两个整数n (1≤n≤2^128) 和r (1≤r≤2^128),分别代表喵的身长和碗的半径。
圆周率使用3.14。
输出描述:
对应每一组数据,如果喵能装进碗里就输出“Yes”;否则输出“No”。
输入
6 1
7 1
9876543210 1234567890
输出
Yes
No
No
1、double
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
double height = scanner.nextDouble();
double r = scanner.nextDouble();
if (2 * 3.14 * r < height) {
System.out.println("No");
} else {
System.out.println("Yes");
}
}
}
}
2、BigDecimal
注意: import java.math.BigDecimal;
import java.util.*;
import java.math.BigDecimal;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
BigDecimal n = scanner.nextBigDecimal();
BigDecimal r = scanner.nextBigDecimal();
BigDecimal len = new BigDecimal("6.28").multiply(r);
// 身长 比 周长 长,进不去
System.out.println(n.compareTo(len) == 1 ? "No" : "Yes");
}
}
}
跳台阶扩展问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶(n为正整数)总共有多少种跳法。
数据范围:1≤n≤20
进阶:空间复杂度 O(1) , 时间复杂度 O(1)
输入描述:
本题输入仅一行,即一个整数 n
输出描述:
输出跳上 n 级台阶的跳法
输入
3
输出
4
【解题思路】
public class Solution {
public int jumpFloorII(int target) {
return 1 << --target;
}
}
官方递归题解:
关于本题,前提是n个台阶会有一次n阶的跳法。分析如下:
f(1) = 1
f(2) = f(2-1) + f(2-2) //f(2-2) 表示2阶一次跳2阶的次数。
f(3) = f(3-1) + f(3-2) + f(3-3)
…
f(n) = f(n-1) + f(n-2) + f(n-3) + … + f(n-(n-1)) + f(n-n)
说明:
1)这里的f(n) 代表的是n个台阶有一次1,2,…n阶的 跳法数。
2)n = 1时,只有1种跳法,f(1) = 1
3) n = 2时,会有两个跳得方式,一次1阶或者2阶,这回归到了问题(1) ,f(2) = f(2-1) + f(2-2)
4) n = 3时,会有三种跳得方式,1阶、2阶、3阶,
那么就是 第一次跳出1阶后面剩下:f(3-1);第一次跳出2阶,剩下f(3-2);第一次3阶,那么剩下f(3-3)
因此结论是f(3) = f(3-1)+f(3-2)+f(3-3)
5) n = n时,会有n中跳的方式, 1阶、2阶...n阶,得出结论:
f(n) = f(n-1)+f(n-2)+…+f(n-(n-1)) + f(n-n) => f(0) + f(1) + f(2) + f(3) + … + f(n-1)
6) 由以上已经是一种结论,但是为了简单,我们可以继续简化:
f(n-1) = f(0) + f(1)+f(2)+f(3) + … + f((n-1)-1) = f(0) + f(1) + f(2) + f(3) + … + f(n-2)
f(n) = f(0) + f(1) + f(2) + f(3) + … + f(n-2) + f(n-1) = f(n-1) + f(n-1)
可以得出:
f(n) = 2*f(n-1)
7) 得出最终结论,在n阶台阶,一次有1、2、…n阶的跳的方式时,总得跳法为:
| 1 ,(n=0 )
f(n) = | 1 ,(n=1 )
| 2*f(n-1),(n>=2)
public class Solution {
public int jumpFloorII(int target) {
if (target <= 0) {
return -1;
} else if (target == 1) {
return 1;
} else {
return 2 * jumpFloorII(target - 1);
}
}
}
三角形
给定三条边,请你判断一下能不能组成一个三角形。
输入描述:
输入包含多组数据,每组数据包含三个正整数a、b、c(1≤a, b, c≤10^100)。
输出描述:
对应每一组数据,如果它们能组成一个三角形,则输出“Yes”;否则,输出“No”。
输入
1 2 3
2 2 2
输出
No
Yes
1、double
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextDouble()) {
double a = scanner.nextDouble();
double b = scanner.nextDouble();
double c = scanner.nextDouble();
if ((a > (c - b)) && (a > (b - c)) && (b > (a - c))) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
}
}
2、BigDecimal
import java.util.*;
import java.math.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
BigDecimal a = scanner.nextBigDecimal();
BigDecimal b = scanner.nextBigDecimal();
BigDecimal c = scanner.nextBigDecimal();
if (a.add(b).compareTo(c) > 0
&& a.add(c).compareTo(b) > 0
&& b.add(c).compareTo(a) > 0) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
}
}
奇数位上都是奇数或者偶数位上都是偶数
import java.util.*;
public class Solution {
public void oddInOddEvenInEven(int[] array) {
int m = 0; // 偶数位
int n = 1; // 奇数位
while (m < array.length && n < array.length) {
if (array[m] % 2 == 0) {
m += 2;
continue;
}
if (array[n] % 2 != 0) {
n += 2;
continue;
}
// 偶数位是奇数 奇数位是偶数 交换
int tmp = array[m];
array[m] = array[n];
array[n] = tmp;
}
}
}
猴子分桃
老猴子辛苦了一辈子,给那群小猴子们留下了一笔巨大的财富——一大堆桃子。老猴子决定把这些桃子分给小猴子。
第一个猴子来了,它把桃子分成五堆,五堆一样多,但还多出一个。它把剩下的一个留给老猴子,自己拿走其中的一堆。
第二个猴子来了,它把桃子分成五堆,五堆一样多,但又多出一个。它把多出的一个留给老猴子,自己拿走其中的一堆。
后来的小猴子都如此照办。最后剩下的桃子全部留给老猴子。
这里有n只小猴子,请你写个程序计算一下在开始时至少有多少个桃子,以及最后老猴子最少能得到几个桃子。
输入描述:
输入包括多组测试数据。
每组测试数据包括一个整数n(1≤n≤20)。
输入以0结束,该行不做处理。
输出描述:
每组测试数据对应一行输出。
包括两个整数a,b。
分别代表开始时最小需要的桃子数,和结束后老猴子最少能得到的桃子数。
输入
5
1
0
输出
3121 1025
1 1
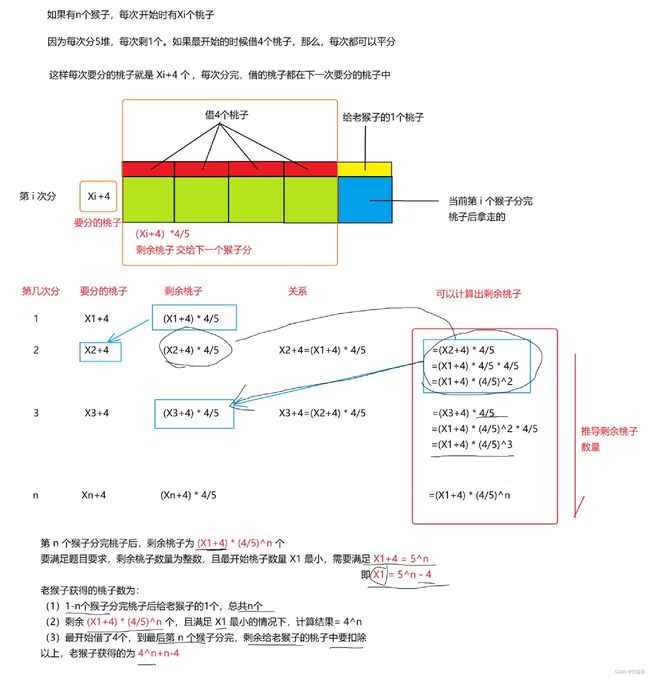
【解题思路】
// write your code here
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
int n = scanner.nextInt();
if (n == 0) break;
long a = (long) (Math.pow(5, n) - 4);
long b = (long) (Math.pow(4, n) + n - 4);
System.out.println(a + " " + b);
}
}
}
有假币
居然有假币! 现在猪肉涨了,但是农民的工资却不见涨啊,没钱怎么买猪肉啊。nowcoder这就去买猪肉,结果找来的零钱中有假币!!!可惜nowcoder 一不小心把它混进了一堆真币里面去了。只知道假币的重量比真币的质量要轻,给你一个天平(天平两端能容纳无限个硬币),请用最快的时间把那个可恶的假币找出来。
输入描述:
1≤n≤2^30,输入0结束程序。
输出描述:
最多要称几次一定能把那个假币找出来?
输入
3
12
0
输出
1
3
【解题思路】
要找到一堆货币中的假币,最快的方式是分三堆,使用其中两堆称重即可
假币比真毕轻,所以:
(1)如果A
(3)如果A=B,那么假币在C
以上将一堆货币分为三份,是最快找到假币的方式
题目问最多需要称几次,那么最坏的情况就是假币每次都在三份最多的那份里边
对于n个货币,n的范围为[1, 2^30],每次分三份,找最多的那份,即为 n/3 向上取整。
如n=4,则分为1,1,2,取最多的2
n=5,则分为2,2,1,取最多的2
解题思路:
对n个货币不停的循环操作,每次分三份,取最大的那份(n/3向上取整),直到n=1或n=2
可以使用 Math.ceil() 方法
需要注意,n/3是int / int,返回值也是int,小数已经丢失了
应该使用: (double)n/3返回一个浮点数,再作为参数传入Math.ceil())方法
即: Math.ceil((double)n/3)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int n = scanner.nextInt();
if (n == 0) {
break;
}
int count = 0;
while (n >= 2) {
n = (int) Math.ceil((double)n / 3);
count++;
}
System.out.println(count);
}
}
}
求正数数组的最小不可组成和 —— 动态规划
给定一个全是正数的数组arr,定义一下arr的最小不可组成和的概念: 1,arr的所有非空子集中,把每个子集内的所有元素加起来会出现很多的值,其中最小的记为min,最大的记为max; 2,在区间[min,max]上,如果有一些正数不可以被arr某一个子集相加得到,那么这些正数中最小的那个,就是arr的最小不可组成和; 3,在区间[min,max]上,如果所有的数都可以被arr的某一个子集相加得到,那么max+1是arr的最小不可组成和; 举例: arr = {3,2,5} arr的min为2,max为10,在区间[2,10]上,4是不能被任何一个子集相加得到的值中最小的,所以4是arr的最小不可组成和; arr = {3,2,4} arr的min为2,max为9,在区间[2,9]上,8是不能被任何一个子集相加得到的值中最小的,所以8是arr的最小不可组成和; arr = {3,1,2} arr的min为1,max为6,在区间[1,6]上,任何数都可以被某一个子集相加得到,所以7是arr的最小不可组成和; 请写函数返回arr的最小不可组成和。
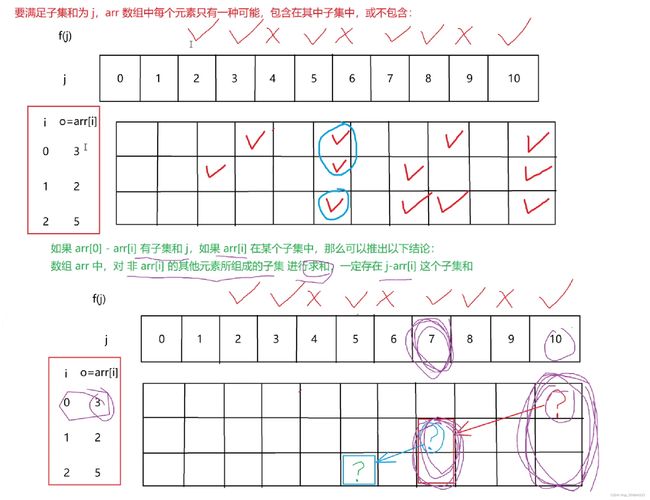
【解题思路】
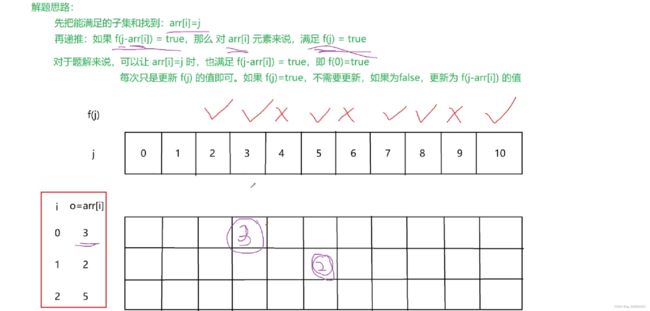
arr = { 3,2,5} 子集及子集求和为
-
{3}=3
-
{2}=2
-
{5}=5
-
{3.2}=5
-
{3,5}=8
-
{2,5}=7
-
{3.2.5}=10
最小子集和为2,最大子集和为10
在[2,10]范围内,最小不可能子集和为4
以 j 表示 arr的可能子集和,即为[2,10]范围内的任一数值,f()表示是否为可能
如:
- f(2) = true
- f(3) = true
- f(4) = false
public class Solution {
/**
* 正数数组中的最小不可组成和
* 输入:正数数组arr
* 返回:正数数组中的最小不可组成和
*/
public int getFirstUnFormedNum(int[] arr) {
int min = Integer.MAX_VALUE;
int max = 0;
for (int i : arr) {
min = Math.min(min, i);
max += i;
}
boolean[] result = new boolean[max + 1];
result[0] = true;
for (int o : arr) { // 遍历数组元素
for (int j = max; j >= o; j--) { // 遍历 max-min 向后往前到 o
result[j] = result[j - o] || result[j]; // 本身就是
}
}
for (int j = min; j < result.length; j++) { // result 中为 false 的就是不可组成
if (!result[j]) {
return j;
}
}
return max + 1;
}
}
最难的问题
NowCoder生活在充满危险和阴谋的年代。为了生存,他首次发明了密码,用于军队的消息传递。假设你是军团中的一名军官,需要把发送来的消息破译出来、并提
供给你的将军。
消息加密的办法是:对消息原文中的每个字母,分别用该字母之后的第5个字母替换(例如:消息原文中的每个字母A 都分别替换成字母F),其他字符不 变,并且消息原文的所有字母都是大写的。密码中的字母与原文中的字母对应关系如下。
密码字母:A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
原文字母:V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
输入描述:
输入包括多组数据,每组数据一行,为收到的密文。
密文仅有空格和大写字母组成。
输出描述:
对应每一组数据,输出解密后的明文。
输入
HELLO WORLD
SNHJ
输出
CZGGJ RJMGY
NICE
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String letters = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
while (scanner.hasNextLine()) {
String s = scanner.nextLine();
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
if (Character.isLetter(s.charAt(i))) {
int index = letters.indexOf(s.charAt(i)); // 在字母串中的位置
index = (index - 5 + 26) % 26; // 前 5 个 字母 ABCDE 对应后面 TUVWX
stringBuilder.append(letters.charAt(index));
} else { // 非字母 不需要转
stringBuilder.append(s.charAt(i));
}
}
System.out.println(stringBuilder.toString());
}
}
}
字符转换操作:
(1) int和char可以互相转换,如:
System.out.println((int)‘A’); // 65
System.out.println((char)68); // D
(2)两个大写字母相减,一定等于转换为int后相减,这样的话,可以得出以下结论:
System.out.println((char) (‘A’ + 2)); // C
System.out.println((char)(‘D’ + 3)); // G
(3)如果相加后的值,不能超出’Z’的值,否则会变为其他字符
如果不是空格,则为大写字母,如果是’E’以后的,拼接为当前字符-5
如果是是’A’- 'E",拼接为当前字符+21
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextLine()) {
String s = scanner.nextLine();
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == ' ') {
stringBuilder.append(" ");
} else {
stringBuilder.append((char) (c > 'E' ? c - 5 : c + 21));
}
}
System.out.println(stringBuilder.toString());
}
}
}
因子个数
一个正整数可以分解成一个或多个数组的积。例如36=223*3,即包含2和3两个因子。NowCoder最近在研究因子个数的分布规律,现在给出一系列正整数,他希望你开发一个程序输出每个正整数的因子个数。
输入描述:
输入包括多组数据。
每组数据仅有一个整数n (2≤n≤100000)。
输出描述:
对应每个整数,输出其因子个数,每个结果占一行。
输入
30
26
20
输出
3
2
2
如何找n的因子是最快的呢?如果有以下关系:
n = x * y
如果x<=y,那么x一定在[2,根号n]的范围内
也就是说,在[2, 根号n] 的范围内,一定能找到n的因子
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int n = scanner.nextInt();
int count = 0;
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
while (n % i == 0) {
n /= i;
}
count++; // 因子的个数
}
}
if (n != 1) { // 素数 再加一
count++;
}
System.out.println(count);
}
}
}
分解因数
所谓因子分解,就是把给定的正整数a,分解成若干个素数的乘积,即 a = a1 × a2 × a3 × … × an,并且 1 < a1 ≤ a2 ≤ a3 ≤ … ≤ an。其中a1、a2、…、an均为素数。 先给出一个整数a,请输出分解后的因子。
输入描述:
输入包含多组数据,每组数据包含一个正整数a(2≤a≤1000000)。
输出描述:
对应每组数据,以“a = a1 * a2 * a3...”的形式输出因式分解后的结果。
输入
10
18
输出
10 = 2 * 5
18 = 2 * 3 * 3
import java.util.*;
public class Main {
private static void AllFactors(int n, List<Integer> factors) {
// 注意等于 10-> 2 * 5 变成5时 如果是小于 退出循环 只有 2
for (int i = 2; i <= n; i++) {
if (n == 0) {
return;
}
while (n != 0 && n % i == 0) {
factors.add(i);
n /= i;
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int n = scanner.nextInt();
List<Integer> factors = new ArrayList<>();
AllFactors(n, factors);
System.out.print(n + " = ");
for (int i = 0; i < factors.size() - 1; i++) {
System.out.print(factors.get(i) + " * ");
}
System.out.println(factors.get(factors.size() - 1));
}
}
}
import java.util.*;
public class Main {
private static List<String> factorization(int a) {
List<String> ans = new ArrayList<>();
for (int i = 2; a > 1 && i * i <= a; i++) {
while (a % i == 0) {
ans.add(String.valueOf(i));
a /= i;
}
}
if (a > 1) {
ans.add(String.valueOf(a));
}
return ans;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int a = scanner.nextInt();
List<String> factors = factorization(a);
System.out.printf("%d = %s\n", a, String.join(" * ", factors));
}
}
}
美国节日
和中国的节日不同,美国的节假日通常是选择某个月的第几个星期几这种形式,因此每一年的放假日期都不相同。具体规则如下:
* 1月1日:元旦
* 1月的第三个星期一:马丁·路德·金纪念日
* 2月的第三个星期一:总统节
* 5月的最后一个星期一:阵亡将士纪念日
* 7月4日:美国国庆
* 9月的第一个星期一:劳动节
* 11月的第四个星期四:感恩节
* 12月25日:圣诞节
现在给出一个年份,请你帮忙生成当年节日的日期。
输入描述:
输入包含多组数据,每组数据包含一个正整数year(2000≤year≤9999)。
输出描述:
对应每一组数据,以“YYYY-MM-DD”格式输出当年所有的节日日期,每个日期占一行。
每组数据之后输出一个空行作为分隔。
输入
2014
2013
输出
2014-01-01
2014-01-20
2014-02-17
2014-05-26
2014-07-04
2014-09-01
2014-11-27
2014-12-25
2013-01-01
2013-01-21
2013-02-18
2013-05-27
2013-07-04
2013-09-02
2013-11-28
2013-12-25
【解析】
问题一:给定 y.m.d,如何得知该天是星期几
以公元前1年12月31日作为基准值,这一天是星期 7
week(y-m-d) 的星期:
间隔天数 % 7,加上 基准的星期,可能是星期7 所以再%7,
间隔天数:
(y-m-d) - (0000-12-31) = 一共多少个整年的天数+最后一年的天数
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = (y - 1)* 365+中间经历多少闰年 * 1+最后一年的天数
[1,y) 所有年中,可以被4整除的有多少:向下取整((y - 1)/4) 而(y - 1)/ 4就是向下取整
可以被100整除:(y -1)/ 100可以被400整除:(y - 1) / 400
(y - 1) / 4 - (y - 1) / 100 +(y - 1) / 400 = 总共经历的闰年数
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = 365* (y - 1) + (y- 1) / 4 - (y- 1) / 100 + (y - 1) / 400+最后一年的天数
化简:365 = 364 +1,364 = 52*7,所以365可以去掉
最后一年的天数:经过的完整月 + day + 闰年 ? 1 : 0
问题二:已知m月的1日是星期w,请问…是哪天
- 已知1月1日星期几,求1月的第三个星期一 :
- 2月的第三个星期一 : 同上
- 已知9月1日星期几,求9月的第一个星期一 :
假设9月1日星期1:答案是就是1,可以写成 1 + 0 * 7 + (7 - w + 1) % 7
对比上面的公式,月份从1月开始,所以是 n - 1,如找第三个星期一,就是 3-1=2 ,得 1 + (n - 1) * 7 + (7 - w + 1) % 7 ,就是 1 + (1 - 1) * 7 + (7 - w + 1) % 7
- 11月的第四个星期四 :
1 + (n - 1) * 7 + (7 - w + 4) % 7 换成 4 即可,就是 1 + (4 - 1) * 7 + (7 - w + 4) % 7
- 公式:
f(w, n, e) = 1 + (n - 1) * 7 + (7 - w + e) % 7
w:本月1号星期几,n:找到本月第几个,e:找星期几
- 5月的最后一个星期一:
代码:
import java.util.*;
public class Main {
private static boolean isLeapYeat(int y) {
return (y % 400 == 0) || (y % 4 == 0 && y % 100 != 0);
}
private static final int[] DAYS = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
// 给定 y,m,d, 返回间隔天数
private static int nDays(int y, int m, int d) {
int n = d;
for (int i = 0; i < m - 1; i++) {
n += DAYS[i];
}
if (m > 2 && isLeapYeat(y)) {
n++;
}
return n;
}
// 传入 y,m,d, 找到从公元前1年 12月31日开始过了多久。求它 MOD 7 的同余数
private static int diff(int y, int m, int d) {
return (y - 1) + (y - 1) / 4 - (y - 1) / 100 + (y - 1) / 400 + nDays(y, m, d);
}
// 根据 y,m,d, 求出星期几
private static int week(int y, int m, int d) {
int w = diff(y, m, d) % 7;
if (w == 0) {
w = 7;
}
return w;
}
// 根据 1 日的星期 w, 求第 n 个星期 e 是几号
private static int m1(int w, int n, int e) {
return 1 + (n - 1) * 7 + (7 - w + e) % 7;
}
// 根据 6月1日星期 w, 求 5月最后一个星期一
private static int m2(int w) {
int d = (w == 1 ? 7 : w - 1);
return 32 - d;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int y = scanner.nextInt();
System.out.printf("%d-01-01\n", y);
int w = week(y, 1, 1);
System.out.printf("%d-01-%02d\n", y, m1(w, 3, 1));
w = week(y, 2, 1);
System.out.printf("%d-02-%02d\n", y, m1(w, 3, 1));
w = week(y, 6, 1);
System.out.printf("%d-05-%02d\n", y, m2(w));
System.out.printf("%d-07-04\n", y);
w = week(y, 9, 1);
System.out.printf("%d-09-%02d\n", y, m1(w, 1, 1));
w = week(y, 11, 1);
System.out.printf("%d-11-%02d\n", y, m1(y, 4, 4));
System.out.printf("%d-12-25\n", y);
System.out.println();
}
}
}
淘宝网店
NowCoder在淘宝上开了一家网店。他发现在月份为素数的时候,当月每天能赚1元;否则每天能赚2元。
现在给你一段时间区间,请你帮他计算总收益有多少。
输入描述:
输入包含多组数据。
每组数据包含两个日期from和to (2000-01-01 ≤ from ≤ to ≤ 2999-12-31)。
日期用三个正整数表示,用空格隔开:year month day。
输出描述:
对应每一组数据,输出在给定的日期范围(包含开始和结束日期)内能赚多少钱。
输入
2000 1 1 2000 1 31
2000 2 1 2000 2 29
输出
62
29
import java.util.Scanner;
public class Main {
private static boolean isPrimeNum(int n) {
if (n == 1) { // 有 1 单独返回
return false;
}
for (int i = 2; i < n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
private static boolean isLeap(int y) {
if (y % 4 == 0 && y % 100 != 0 || y % 400 == 0) {
return true;
}
return false;
}
private static int income(int fromYear, int fromMonth, int fromDay, int toYear, int toMonth, int toDay) {
int income = 0;
int[] monthDays = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
if (isLeap(fromYear)) { // 起始年 是闰年
monthDays[1] = 29;
}
// 1、同一年 单独计算
if (fromYear == toYear) {
// fromMonth - toMonth-1
for (int i = fromMonth; i < toMonth; i++) {
if (isPrimeNum(i)) {
income += monthDays[i - 1];
} else {
income += monthDays[i - 1] * 2;
}
}
// 只有一个月 fromDay - toDay
income += isPrimeNum(fromMonth) ? toDay - fromDay + 1: (toDay - fromDay + 1) * 2;
return income;
}
// 计算起始年 fromMont - 12 的收益
if (isPrimeNum(fromMonth)) { // fromMonth 可能不是从第一天开始
income += monthDays[fromMonth - 1] - fromDay + 1;
} else {
income += (monthDays[fromMonth - 1] - fromDay + 1) * 2;
}
for (int i = fromMonth + 1; i <= 12; i++) { // fromMonth - 12
if (isPrimeNum(i)) {
income += monthDays[i - 1];
} else {
income += monthDays[i - 1] * 2;
}
}
// 结束年不是闰年 改回 28
if (!isLeap(toYear)) {
monthDays[1] = 28;
}
// 计算结束年 1 - toMonth-1 的收益
for (int i = 1; i < toMonth; i++) { // 结束年 月
if (isPrimeNum(i)) {
income += monthDays[i - 1];
} else {
income += monthDays[i - 1] * 2;
}
}
// toMonth 的 toDay 收益
income += isPrimeNum(toMonth) ? toDay : toDay * 2; // 结束年 日
// 2、相隔一年 返回
if (fromYear + 1 == toYear) {
return income;
}
// 3、相隔多年 加中间年
monthDays[1] = 28; // 改回 28
// 2000 - 2002 ---> 2001-2001 需要取等于
for (int i = fromYear + 1; i <= toYear - 1; i++) {
if (isLeap(i)) {
monthDays[1] = 29;
} else {
monthDays[1] = 28;
}
for (int j = 1; j <= 12; j++) {
if (isPrimeNum(j)) {
income += monthDays[j - 1];
} else {
income += monthDays[j - 1] * 2;
}
}
}
return income;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
// 2000 1 1 2999 12 31 579243
int fromYear = scanner.nextInt();
int fromMonth = scanner.nextInt();
int fromDay = scanner.nextInt();
int toYear = scanner.nextInt();
int toMonth = scanner.nextInt();
int toDay = scanner.nextInt();
int income = income(fromYear, fromMonth, fromDay, toYear, toMonth, toDay);
System.out.println(income);
}
}
}
import java.util.Scanner;
public class Main {
private static boolean isLeap(int y) {
return (y % 4 == 0 && y % 100 != 0 || y % 400 == 0);
}
// 给定一年 整年的收益
private static int annualIncome(int year) {
return 2 * 31
+ 28
+ 31
+ 2 * 30
+ 31
+ 2 * 30
+ 31
+ 2 * 31
+ 2 * 30
+ 2 * 31
+ 30
+ 2 * 31
+ (isLeap(year) ? 1 : 0);
}
private static boolean isPrime(int month) {
return month == 2 || month == 3 || month == 5 || month == 7 || month == 11;
}
// 从一年1月1日 到这一年 m,d 的收益
private static int profitThisYear(int year, int month, int day) {
int profit = 0;
if (!isPrime(month)) {
profit = day * 2;
} else {
profit = day;
}
while (--month > 0) {
switch(month) {
case 1: case 8: case 10: case 12:
profit += 62;
break;
case 3: case 5: case 7:
profit += 31;
break;
case 4: case 6: case 9:
profit += 60;
break;
case 11:
profit += 30;
break;
default: // 2 月
profit += (28 + (isLeap(year) ? 1 : 0));
break;
}
}
return profit;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int fromYear = scanner.nextInt();
int fromMonth = scanner.nextInt();
int fromDay = scanner.nextInt();
int toYear = scanner.nextInt();
int toMonth = scanner.nextInt();
int toDay = scanner.nextInt();
int profit = 0;
// 起始年:整年 - 到fromDay之间 (注意减一)
profit = annualIncome(fromYear) - profitThisYear(fromYear, fromMonth, fromDay - 1);
// 同一年 2000 5 17 2000 7 1
// —> 5.17到12.31的收益 - 全年
// = 负的一月一号到5.16的收益 + 加后面结束年
// = 负的一月一号到5.16的收益 + 一月一号到7.1
// = 5.17 - 7.1 的收益
if (fromYear == toYear) {
profit -= annualIncome(fromYear);
}
// 结束年
profit += profitThisYear(toYear, toMonth, toDay);
// 中间年
for (int i = fromYear + 1; i < toYear; i++) {
profit += annualIncome(i);
}
System.out.println(profit);
}
}
}
斐波那契凤尾
NowCoder号称自己已经记住了1-100000之间所有的斐波那契数。
为了考验他,我们随便出一个数n,让他说出第n个斐波那契数。当然,斐波那契数会很大。因此,如果第n个斐波那契数不到6位,则说出该数;否则只说出最后6位。
输入描述:
输入有多组数据。
每组数据一行,包含一个整数n (1≤n≤100000)。
输出描述:
对应每一组输入,输出第n个斐波那契数的最后6位。
输入
1
2
3
4
100000
输出
1
2
3
5
537501
// write your code here
import java.util.*;
public class Main {
public static void main(String[] args) {
int border = -1;
int[] array = new int[100000];
array[0] = 1;
array[1] = 2;
for (int i = 2; i < 100000; i++) {
array[i] = array[i - 1] + array[i - 2];
if (border == -1 && array[i] >= 1000000) { // 超过6位数 记录
border = i + 1;
}
array[i] %= 1000000; // 用 border,后取模
}
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int n = scanner.nextInt();
if (n < border) {
System.out.printf(array[n - 1]);
} else {
System.out.printf("%06d\n", array[n - 1]);
}
}
}
public static void main1(String[] args) {
// 提前计算
int[] array = new int[100000];
array[0] = 1;
array[1] = 2;
for (int i = 2; i < 100000; i++) {
array[i] = (array[i - 1] + array[i - 2]) % 1000000;
}
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int n = scanner.nextInt();
// 补 0
System.out.printf(n < 25 ? "%d\n" : "%06d\n", array[n - 1]);
}
}
}
剪花布条
一块花布条,里面有些图案,另有一块直接可用的小饰条,里面也有一些图案。对于给定的花布条和小饰条,计算一下能从花布条中尽可能剪出几块小饰条来呢?
输入描述:
输入包含多组数据。
每组数据包含两个字符串s,t,分别是成对出现的花布条和小饰条,其布条都是用可见ASCII字符表示的,可见的ASCII字符有多少个,布条的花纹也有多少种花样。花纹条和小饰条不会超过1000个字符长。
输出描述:
对应每组输入,输出能从花纹布中剪出的最多小饰条个数,如果一块都没有,那就输出0,每个结果占一行。
输入
abcde a3
aaaaaa aa
输出
0
3
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
String s = scanner.next();
String t = scanner.next();
int count = 0;
while (s.contains(t)) {
s = s.replaceFirst(t, ""); // replaceFirst 替换第一个
count++;
}
System.out.println(count);
}
}
}